Для стального вала круглого сплошного сечения заданной схемы (табл. 4.1) требуется:
1) построить эпюру крутящих моментов;
2) подобрать диаметр вала из условия прочности при заданном значении допускаемого напряжения [ τ ] и из условия жёсткости при заданном значении допускаемого угла закручивания [ φ ] на 1 метре длины вала; из полученных двух значений диаметра назначить больший;
3) построить эпюры касательных напряжений по длине вала;
4) приняв модуль сдвига G =8*104 МПа, определить углы закручивания всех участков вала и построить эпюру углов поворота по длине вала;
5) вычислить потенциальную энергию упругой деформации вала U и работу внешних сил А; при расхождении этих величин более, чем на 1% следует уточнить расчет или найти ошибки.
Допущения:
– При построении эпюры углов поворота считать заделанный конец вала не поворачивающимся. Угол поворота произвольного сечения равен сумме углов закручивания на длине от заделки до сечения, взятой со знаком “ + ” при заделанном левом конце и со знаком “ – ” при заделанном правом конце.
– Надо помнить, что потенциальная энергия вала на всех участках положительна, а работа приложенных извне моментов положительна, если совпадают направления этих моментов и углов, поворота сечений, в которых моменты приложены, и отрицательна, если эти направления противоположны.
Необходимые для расчета данные приведены в таблице 4.2.
Таблица 4.1
| 1. | 
| 2. | 
|
| 3. | 
| 4. | 
|
| 5. | 
| 6. | 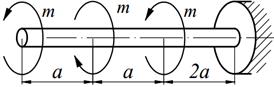
|
| 7. | 
| 8. | 
|
| 9. | 
| 10. | 
|
| 11. | 
| 12. | 
|
| 13. | 
| 14. | 
|
| 15. | 
| 16. | 
|
| 17. | 
| 18. | 
|
| 19. | 
| 20. | 
|
| 21. | 
| 22. | 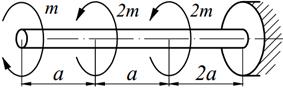
|
| 23. | 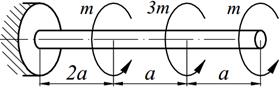
| 24. | 
|
| 25. | 
| 26. | 
|
Таблица 4.2
| № варианта | m, кНм | а, м | [ τ ], МПа | [ φ ], град/м |
| 1. | 0,2 | |||
| 2. | 0,4 | |||
| 3. | 0,6 | |||
| 4. | 0,8 | |||
| 5. | 1,0 | |||
| 6. | 2,0 | |||
| 7. | 1,8 | |||
| 8. | 1,6 | |||
| 9. | 1,4 | |||
| 10. | 1,2 |
Задание №5. Расчет на прямой изгиб балок с двумя опорами
Для заданных балок (табл. 5.1) требуется: написать выражения Q и M для каждого участка в общем виде, построить эпюры Q и M, найти | M |max и подобрать (определить диаметр) деревянную балку круглого поперечного сечения при [σ] = 10 МПа.
Необходимые для расчета данные приведены в таблице 5.2.
Таблица 5.1
| 1. | 
| 2. | 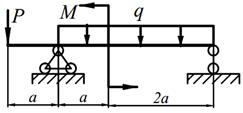
|
| 3. | 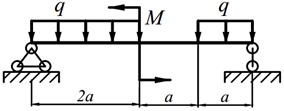
| 4. | 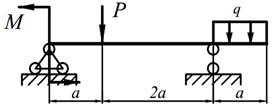
|
| 5. | 
| 6. | 
|
| 7. | 
| 8. | 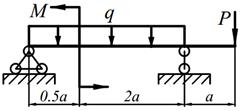
|
| 9. | 
| 10. | 
|
| 11. | 
| 12. | 
|
| 13. | 
| 14. | 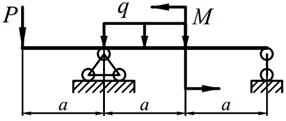
|
| 15. | 
| 16. | 
|
| 17. | 
| 18. | 
|
| 19. | 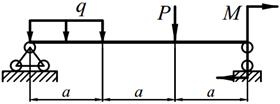
| 20. | 
|
| 21. | 
| 22. | 
|
| 23. | 
| 24. | 
|
| 25. | 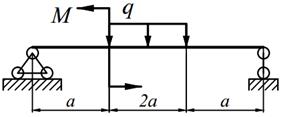
| 26. | 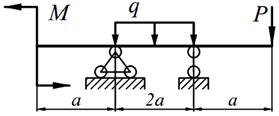
|
Таблица 5.2
| № варианта | Р [кН] | q [кН/м] | М [кНм] | а [м] |
| 1. | ||||
| 2. | ||||
| 3. | ||||
| 4. | ||||
| 5. | ||||
| 6. | ||||
| 7. | ||||
| 8. | ||||
| 9. | ||||
| 10. |
Задание №6. Расчет на прямой изгиб балок с жесткой заделкой
Для заданных балок (табл. 6.1) требуется:
1. написать выражения Q и M для каждого участка в общем виде, построить эпюры Q и M, найти | M |max и подобрать стальные балки прямоугольного поперечного сечения с заданным отношением «k » высоты к ширине и двутавр при [ σ ] = 160 МПа.
2. определить прогиб и угол поворота консольного конца балки, приняв значения модулей упругости для стали Е ст = 2·105 МПа и для древесины Е др = 104 МПа.
Необходимые для расчета данные приведены в таблице 6.2.
Таблица 6.1
| 1. | 
| 2. | 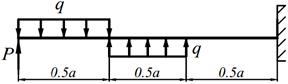
|
| 3. | 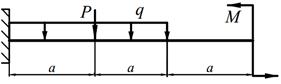
| 4. | 
|
| 5. | 
| 6. | 
|
| 7. | 
| 8. | 
|
| 9. | 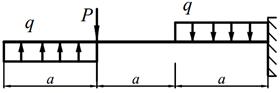
| 10. | 
|
| 11. | 
| 12. | 
|
| 13. | 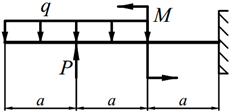
| 14. | 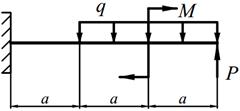
|
| 15. | 
| 16. | 
|
| 17. | 
| 18. | 
|
| 19. | 
| 20. | 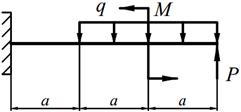
|
| 21. | 
| 22. | 
|
| 23. | 
| 24. | 
|
| 25. | 
| 26. | 
|
Таблица 6.2
| № варианта | Р [кН] | q [кН/м] | М [кНм] | а [м] | k |
| 1. | |||||
| 2. | 1,5 | ||||
| 3. | |||||
| 4. | |||||
| 5. | 1,5 | ||||
| 6. | |||||
| 7. | |||||
| 8. | 1,5 | ||||
| 9. | |||||
| 10. |
Задание №7. Расчет статически определимых плоских рам на прямой изгиб
Для заданных рам (табл. 7.1) требуется: написать выражения N, Q и M для каждого участка в общем виде, построить эпюры N, Q и M, найти | M |max и подобрать стальную раму двутаврового поперечного сечения при [σ] = 160 МПа;
Необходимые для расчета данные приведены в таблице 7.2.
Таблица 7.1
| 1. | 
| 2. | 
|
| 3. | 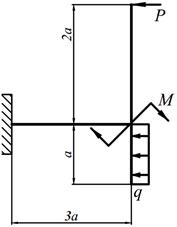
| 4. | 
|
| 5. | 
| 6. | 
|
| 7. | 
| 8. | 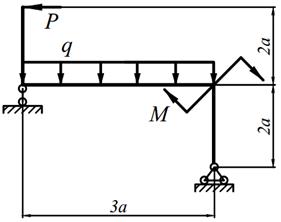
|
| 9. | 
| 10. | 
|
| 11. | 
| 12. | 
|
| 13. | 
| 14. | 
|
| 15. | 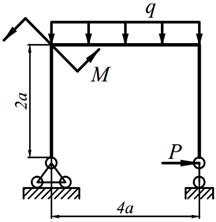
| 16. | 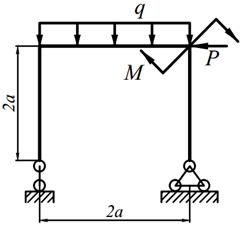
|
| 17. | 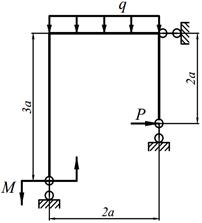
| 18. | 
|
| 19. | 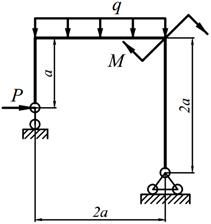
| 20. | 
|
| 21. | 
| 22. | 
|
| 23. | 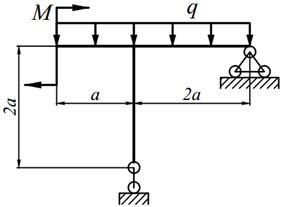
| 24. | 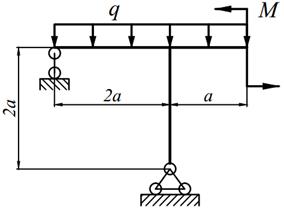
|
| 25. | 
| 26. | 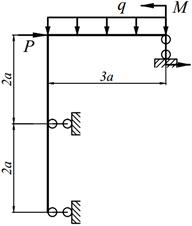
|
Таблица 7.2
| № варианта | Р [кН] | q [кН/м] | М [кНм] | а [м] |
| 1. | ||||
| 2. | ||||
| 3. | ||||
| 4. | ||||
| 5. | ||||
| 6. | ||||
| 7. | ||||
| 8. | ||||
| 9. | ||||
| 10. |
Задание №8. Геометрические характеристики плоского
Поперечного сечения
Для заданного поперечного сечения, состоящего из двух элементов (табл. 8.1) требуется:
1. определить положение центра тяжести;
2. вычислить значения осевых и центробежного моментов инерции сечения относительно горизонтальной и вертикальной осей, проходящих через центр тяжести;
3. найти положение главных центральных осей инерции;
4. определить величины моментов инерции относительно главных цен тральных осей;
5. вычертить сечение в масштабе 1: 2, обозначив на нем все оси и численные значения размеров.
Необходимые для расчета данные приведены в таблице 8.2.
Таблица 8.1
| 1. | 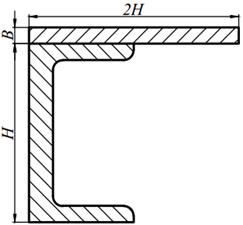
| 2. | 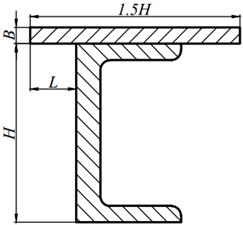
|
| 3. | 
| 4. | 
|
| 5. | 
| 6. | 
|
| 7. | 
| 8. | 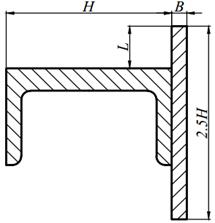
|
| 9. | 
| 10. | 
|
| 11. | 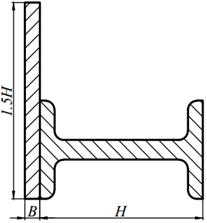
| 12. | 
|
| 13. | 
| 14. | 6 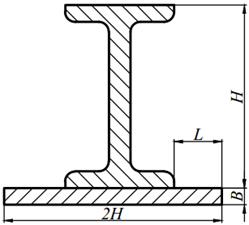
|
| 15. | 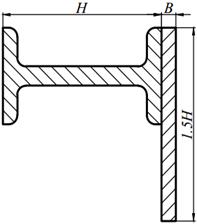
| 16. | 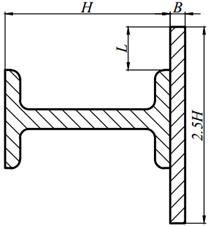
|
| 17. | 
| 18. | 
|
| 19. | 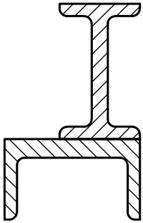
| 20. | 
|
| 21. | 
| 22. | 
|
| 23. | 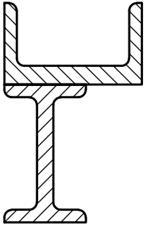
| 24. | 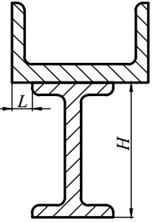
|
| 25. | 
| 26. | 
|
Таблица 8.2
| № Вариантов | № Двутавра | № Швеллера | B, мм | K = L/H |
| 1. | 0.4 | |||
| 2. | 0.5 | |||
| 3. | 0.6 | |||
| 4. | 0.7 | |||
| 5. | 0.8 | |||
| 6. | 1.0 | |||
| 7. | 0.1 | |||
| 8. | 0.2 | |||
| 9. | 0.3 | |||
| 10. | 0.4 |