1. Определить степень статической неопределимости рамы.
2. Выбрать основную систему.
3. Составить канонические уравнения метода сил.
4. Построить в основной системе эпюры изгибающих моментов от действия фиктивных единичных сил и заданной нагрузки.
5. Вычислить единичные и грузовые перемещения, применяя способ Верещагина. Проверить вычисленные перемещения с помощью суммарной единичной эпюры (Мs).
6. Решить систему канонических уравнений и проверить правильность определения «лишних» неизвестных.
7. Построить окончательную эпюру изгибающих моментов (М). Произвести кинематическую проверку эпюры М путём перемножения эторы М с единичными эпюрами; результат каждого перемножения должен равняться нулю с ошибкой не более 1%; количество проверок должно соответствовать степени статической неопределимости рамы.
8. Построить эпюры поперечных (Q) и продольных (N) сил и произвести статическую проверку.
9. Произведение ЕI считать постоянным (ЕI = const).
Варианты заданий представлены в табл. 12.1, необходимые для расчета данные приведены в таблице 12.2.
Таблица 12.1
| 1. | 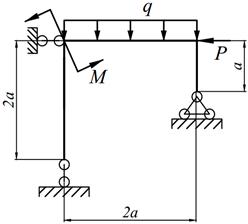
| 2. | 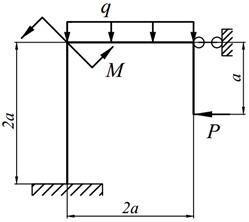
|
| 3. | 
| 4. | 
|
| 5. | 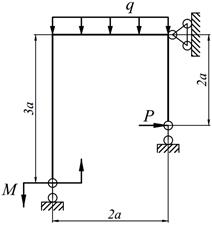
| 6. | 
|
| 7. | 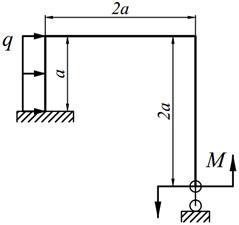
| 8. | 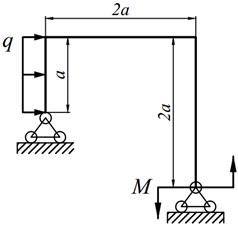
|
| 9. | 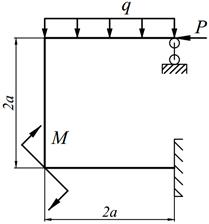
| 10. | 
|
| 11. | 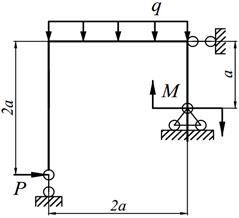
| 12. | 
|
| 13. | 
| 14. | 
|
| 15. | 
| 16. | 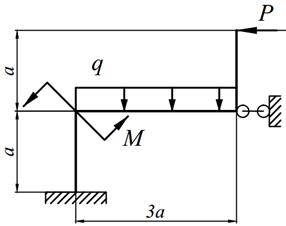
|
| 17. | 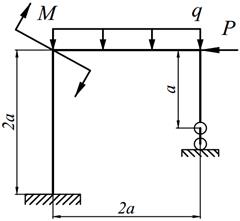
| 18. | 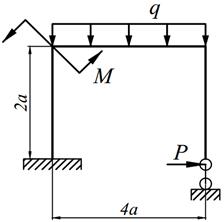
|
| 19. | 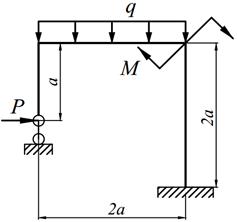
| 20. | 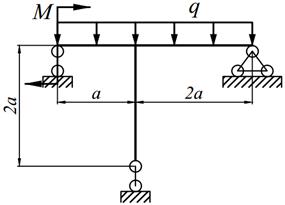
|
| 21. | 
| 22. | 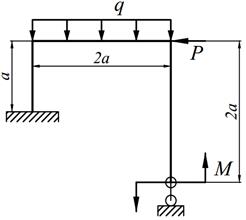
|
| 23. | 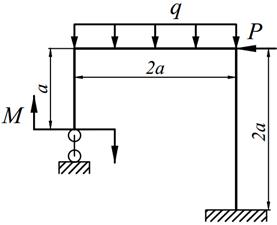
| 24. | 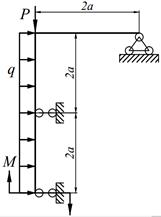
|
| 25. | 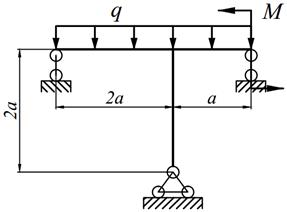
| 26. | 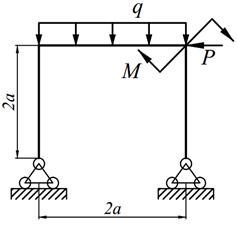
|
Таблица 12.2
| № вариантов | М [кНм] | Р [кН] | q [кН/м] |
| 1. | |||
| 2. | |||
| 3. | |||
| 4. | |||
| 5. | |||
| 6. | |||
| 7. | |||
| 8. | |||
| 9. | |||
| 10. |
Задание №13. Подбор сечения сжатого стержня с учётом коэффициента устойчивости
Подобрать сечения стальной стойки, сжатой силой Р, если основное допускаемое напряжение на сжатие для стали равно [ σ ]=160МПа. Расчет производить методом последовательных приближений, первоначально задавшись коэффициентом φ =0,5.
Варианты заданий представлены в табл. 13.1, необходимые для расчета данные приведены в таблице 13.2.
Таблица 13.1
| 1. | 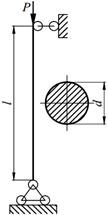
| 2. | 
| 3. | 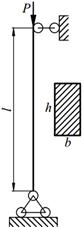
| 4. | 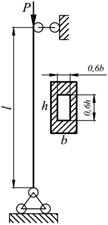
|
| 5. | 
| 6. | 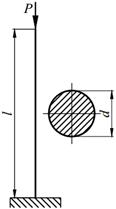
| 7. | 
| 8. | 6 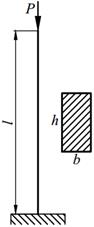
|
| 9. | 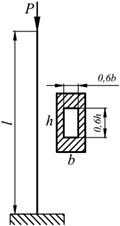
| 10. | 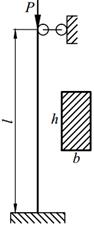
| 11. | 
| 12. | 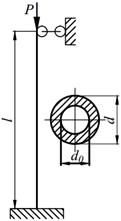
|
| 13. | 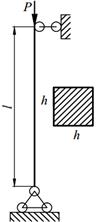
| 14. | 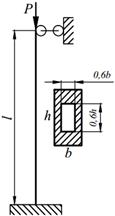
| 15. | 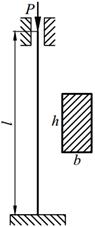
| 16. | 
|
| 17. | 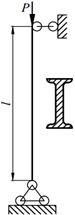
| 18. | 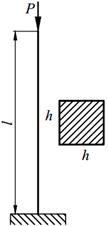
| 19. | 
| 20. | 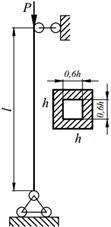
|
| 21. | 
| 22. | 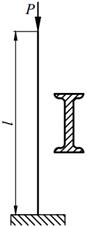
| 23. | 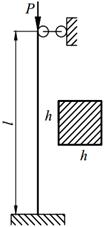
| 24. | 
|
| 25. | 
| 26. | 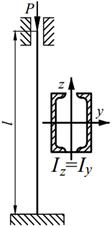
| 27. | 
| 28. | 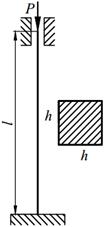
|
Таблица 13.2
| № вариантов | P, [кН] | l,[м] | 
| 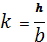
|
| 0,5 | 0,7 | 1,15 | ||
| 0,6 | 0,8 | 1,20 | ||
| 0,7 | 0,9 | 1,25 | ||
| 0,8 | 0,7 | 1,30 | ||
| 0,9 | 0,8 | 1,35 | ||
| 1,0 | 0,9 | 1,40 | ||
| 1,1 | 0,7 | 1,45 | ||
| 1,2 | 0,8 | 1,50 | ||
| 1,3 | 0,9 | 1,55 | ||
| 1,4 | 0,7 | 1,60 |
Задание №14. Расчет балок на действие ударной нагрузки
Груз массой m падает на двутавровую балку АВ с высоты h. Для уменьшения динамического воздействия падающего груза на балку устанавливается в отдельных точках балки пружины с жесткостью с. Определить максимальную высоту падения груза hmax при условии, что максимальные напряжения не должны превышать значение [σ]=160МПа. Задачу решить в предложении отсутствия пружин и при их наличии. Сравнить полученные значения hmax .
Варианты заданий представлены в табл. 14.1, необходимые для расчета данные приведены в таблице 14.2.
Таблица 14.1
| 1. | 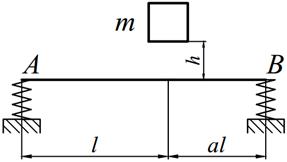
| 2. | 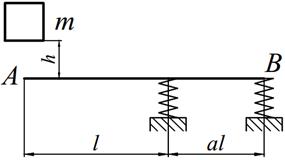
|
| 3. | 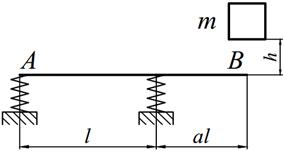
| 4. | 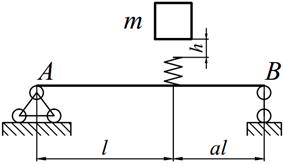
|
| 5. | 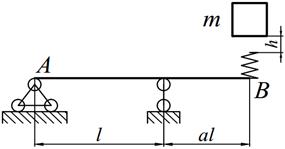
| 6. | 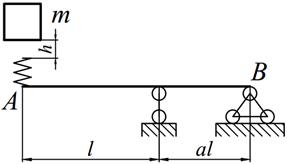
|
| 7. | 
| 8. | 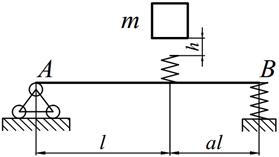
|
| 9. | 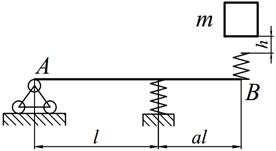
| 10. | 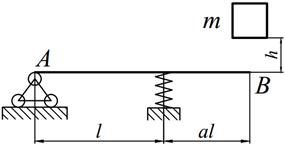
|
| 11. | 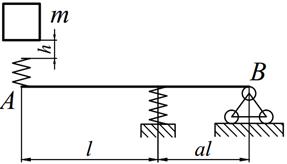
| 12. | 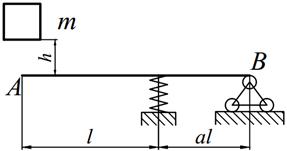
|
| 13. | 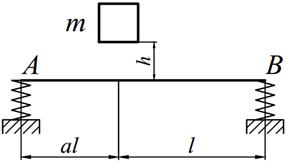
| 14. | 
|
| 15. | 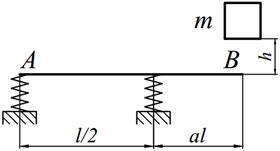
| 16. | 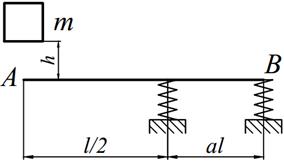
|
| 17. | 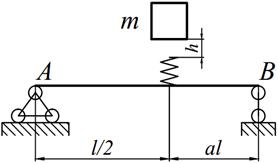
| 18. | 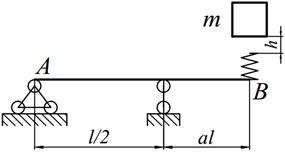
|
| 19. | 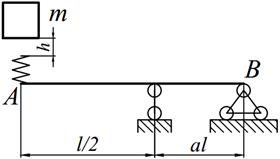
| 20. | 
|
| 21. | 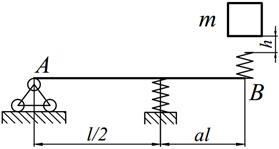
| 22. | 
|
| 23. | 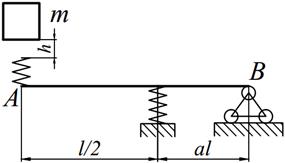
| 24. | 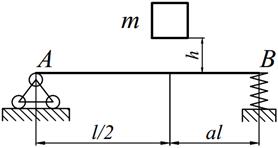
|
| 25. | 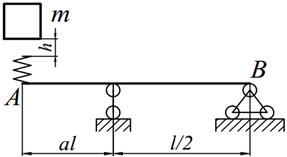
| 26. | 
|
Таблица 14.2
| № вариантов | m, [кг] | l, [м] | а | № двутавра | с,[кН/м] |
| 1. | 1,0 | 0,9 | |||
| 2. | 1,2 | 0,8 | |||
| 3. | 1,4 | 0,7 | |||
| 4. | 1,6 | 0,6 | |||
| 5. | 1,8 | 0,5 | |||
| 6. | 2,0 | 0,4 | |||
| 7. | 2,2 | 0,3 | 20а | ||
| 8. | 2,4 | 0,2 | |||
| 9. | 2,6 | 0,5 | |||
| 10. | 2,8 | 0,4 |
Задание №15. Расчет балок на «отстройку» от резонанса с определением динамических напряжений
Двигатель массой М укреплен на балке АВ, состоящей из двух швеллеров. Угловая скорость вращения вала двигателя равна ω. Определить значение l, при котором будет наблюдаться резонанс системы. Принимая частоту вынуждены колебаний равной 70% от частоты свободных колебаний определить длину балки, обеспечивающую отстройку от резонанса. Построить график изменения во времени напряжений изгиба балки, если масса дисбаланса равна m 0 а её смещение от центра вращения равно е. Определить коэффициенты ассиметрии цикла.
Варианты заданий представлены в табл. 15.1, необходимые для расчета данные приведены в таблице 15.2.
Таблица 15.1
| 1. | 
| 2. | 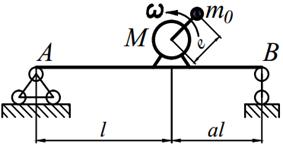
|
| 3. | 
| 4. | 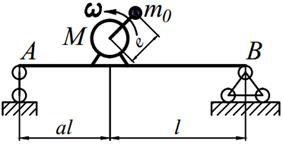
|
| 5. | 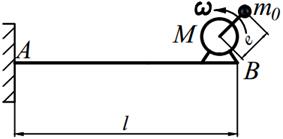
| 6. | 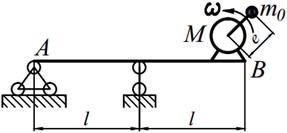
|
| 7. | 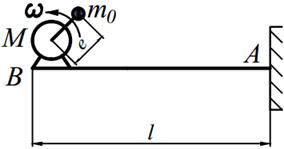
| 8. | 
|
| 9. | 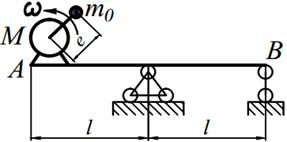
| 10. | 
|
| 11. | 
| 12. | 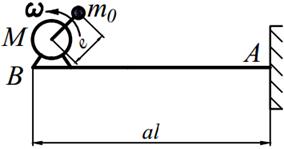
|
| 13. | 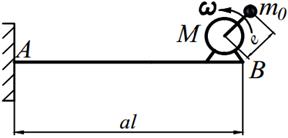
| 14. | 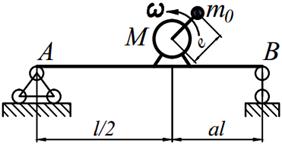
|
| 15. | 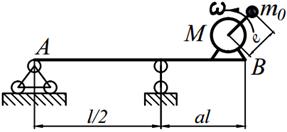
| 16. | 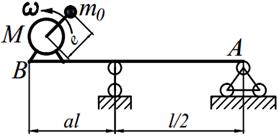
|
| 17. | 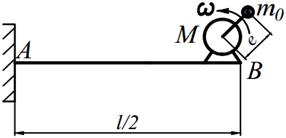
| 18. | 
|
| 19. | 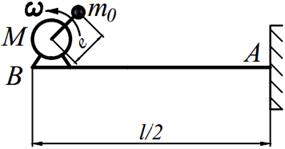
| 20. | 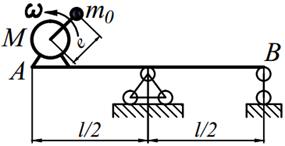
|
| 21. | 
| 22. | 
|
| 23. | 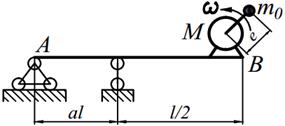
| 24. | 
|
| 25. | 
| 26. | 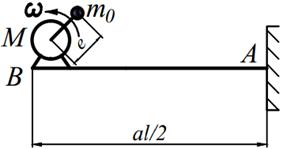
|
Таблица 15.2
| № вариантов | М, [кг] | m 0, [кг] | ω,[рад/с] | e, [мм] | a | № швеллеров |
| 1. | 1,0 | 0,2 | ||||
| 2. | 1,2 | 0,3 | ||||
| 3. | 1,4 | 0,4 | ||||
| 4. | 1,6 | 0,5 | ||||
| 5. | 1,8 | 0,6 | ||||
| 6. | 2,0 | 0,7 | ||||
| 7. | 2,2 | 0,8 | ||||
| 8. | 2,4 | 0,9 | ||||
| 9. | 0,4 | |||||
| 10. | 0,5 |