Для короткого чугунного стержня заданного поперечного сечения, состоящего из нескольких простых фигур (табл. 9.1) сжимаемого силой P, приложенной в точке A и направленной параллельно оси стержня требуется:
1. вычислить главные центральные моменты инерции сечения и квадраты главных радиусов инерции;
2. найти отрезки, отсекаемые нулевой линией на главных центральных осях инерции;
3. вычертить в масштабе сечение, показать на чертеже нулевую линию и установить точки сечения, в которых действуют наибольшие напряжения растяжения и сжатия;
4. определить эти напряжения, выразив их через P и геометрические характеристики сечения;
5. найти допускаемую нагрузку [ P ] при заданных допускаемых напряжениях для чугуна на растяжение [σр] и на сжатие [σс];
6. вычислить напряжение в точках А, Б и B от действия допускаемой нагрузки;
7. построить эпюру напряжений в аксонометрии;
8. построить ядро сечения.
Необходимые для расчета данные приведены в таблице 9.2
Таблица 9.1
| 1. | 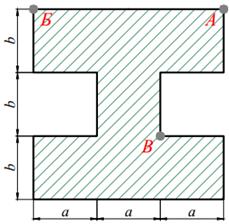
| 2. | 
|
| 3. | 
| 4. | 
|
| 5. | 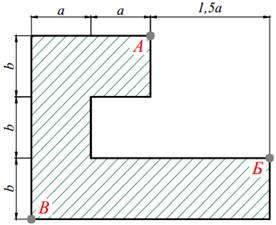
| 6. | 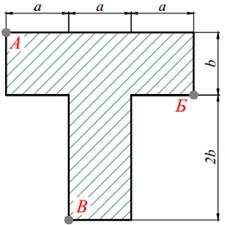
|
| 7. | 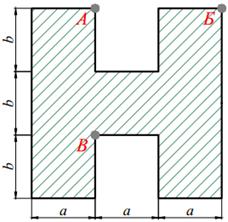
| 8. | 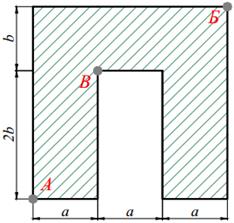
|
| 9. | 
| 10. | 
|
| 11. | 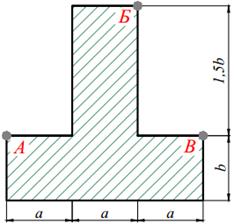
| 12. | 
|
| 13. | 
| 14. | 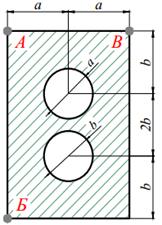
|
| 15. | 
| 16. | 
|
| 17. | 
| 18. | 
|
| 19. | 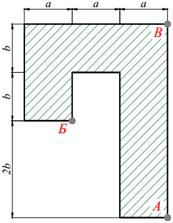
| 20. | 
|
| 21. | 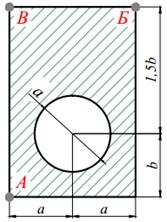
| 22. | 
|
| 23. | 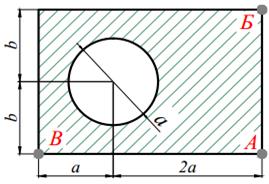
| 24. | 
|
| 25. | 
| 26. | 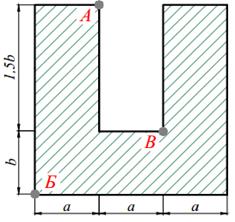
|
Таблица 9.2
| № | P [кН] | a [см] | b [см] |
Задание №10. Расчет балок на косой изгиб
Деревянная балка прямоугольного поперечного сечения с шириной b и высотой h нагружена в вертикальной плоскости силами Р, равномерно распределённой нагрузкой q и моментом M (табл. 10.1), а в горизонтальной плоскости силой Р приложенной в точке D (направленной влево, если смотреть с левого торца балки). На опорах балки могут возникнуть как вертикальные, так и горизонтальные реакции, направленные перпендикулярно плоскости чертежа. Внешние нагрузки действуют по оси балки.
Требуется:
1) Построить эпюры изгибающих моментов в вертикальной М верт. и горизонтальной М гор. плоскостях, установить положение опасного сечения;
2) Подобрать размеры поперечного сечения b и h с заданным отношением «k » высоты к ширине, при допускаемом напряжении [σ]=10 МПа;
3) Определить положение нейтральной линии в опасном сечении балки и построить для этого сечения эпюру нормальных напряжений в аксонометрии.
Необходимые для расчета данные приведены в таблице 10.2.
Таблица 10.1
| 1. | 
| 2. | 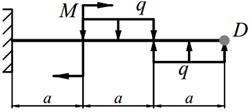
|
| 3. | 
| 4. | 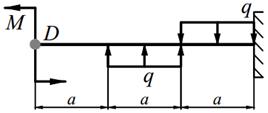
|
| 5. | 
| 6. | 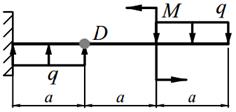
|
| 7. | 
| 8. | 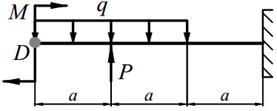
|
| 9. | 
| 10. | 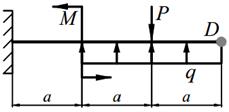
|
| 11. | 
| 12. | 
|
| 13. | 
| 14. | 
|
| 15. | 
| 16. | 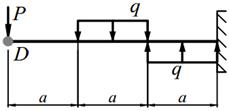
|
| 17. | 
| 18. | 
|
| 19. | 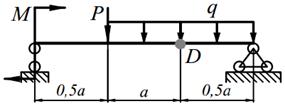
| 20. | 
|
| 21. | 
| 22. | 
|
| 23. | 
| 24. | 
|
| 25. | 
| 26. | 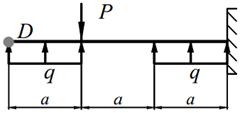
|
Таблица 10.2
| № варианта | Р [кН] | q [кН/м] | М [кНм] | а [м] | k |
| 1. | |||||
| 2. | 1,5 | ||||
| 3. | |||||
| 4. | |||||
| 5. | 1,5 | ||||
| 6. | |||||
| 7. | |||||
| 8. | 1,5 | ||||
| 9. | |||||
| 10. |
Задание №11. Расчет бруса круглого поперечного сечения
На изгиб с кручением
На вал круглого сечения диаметром D (табл. 11.1) по участкам действуют одновременно крутящие моменты М, вертикальные и горизонтальные силы P.
Требуется:
1. Построить эпюры:
a) крутящих моментов M к;
b) эпюры изгибающих моментов в вертикальной плоскости M в;
c) эпюры изгибающих моментов в горизонтальной плоскости Мг;
d) построить эпюру суммарных изгибающих моментов Ми;
2. Рассматривая эпюру M к и M и, найти опасное сечение и определить величину максимального расчетного момента по третьей теории прочности;
3. По полученному расчетному моменту Мр подобрать диаметр вала D при [σ] = 70 МПа.
Варианты заданий представлены в табл. 11.1, необходимые для расчета данные приведены в таблице 11.2.
Таблица 11.1
| 1. | 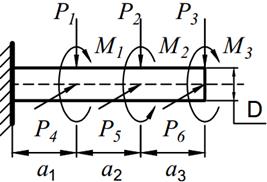
| 2. | 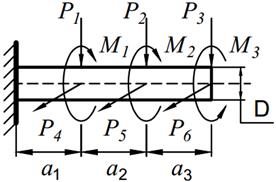
|
| 3. | 
| 4. | 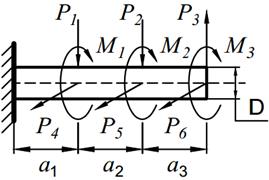
|
| 5. | 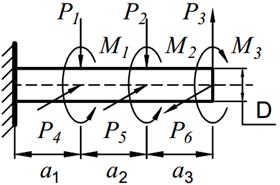
| 6. | 
|
| 7. | 
| 8. | 
|
| 9. | 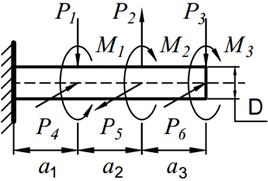
| 10. | 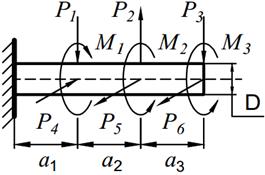
|
| 11. | 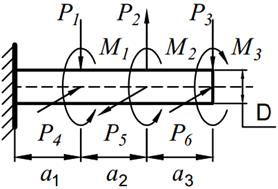
| 12. | 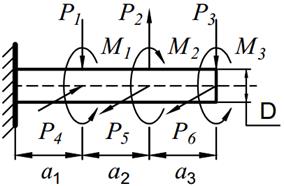
|
| 13. | 
| 14. | 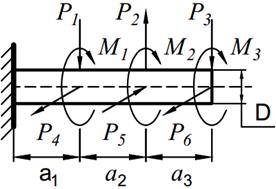
|
| 15. | 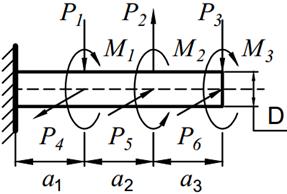
| 16. | 
|
| 17. | 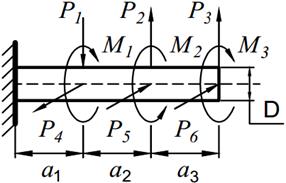
| 18. | 
|
| 19. | 
| 20. | 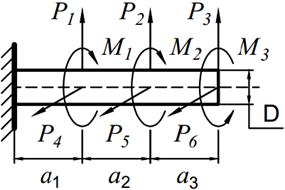
|
| 21. | 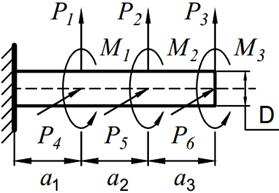
| 22. | 
|
| 23. | 
| 24. | 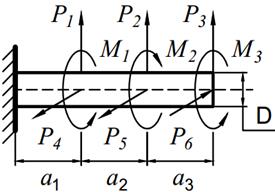
|
| 25. | 
| 26. | 
|
Таблица 11.2
| № вариантов | М1 [кНм] | М2 [кНм] | М3 [кНм] | P 1 [кН] | P 2 [кН] | P 3 [кН] | P 4 [кН] | P 5 [кН] | P 6 [кН] | a 1, [м] | a 2, [м] | a 3, [м] |
| 1. | 1,2 | 1,4 | ||||||||||
| 2. | 1,2 | 1,4 | 1,6 | |||||||||
| 3. | 1,4 | 1,6 | 1,8 | |||||||||
| 4. | 1,6 | 1,8 | ||||||||||
| 5. | 1,8 | 2,2 | ||||||||||
| 6. | 2,2 | 2,4 | ||||||||||
| 7. | 2,2 | 2,4 | 2,6 | |||||||||
| 8. | 2,4 | 2,6 | 2,8 | |||||||||
| 9. | 2,6 | 2,8 | ||||||||||
| 10. | 2,8 | 1,2 |
Задание №12. Расчет статически неопределимой рамы методом сил
Оформление работы
Задание выполняется в отдельной тетради или на скрепленных между собой листов бумаги формата А4, в которой должны отражаться все необходимые расчёты. Схемы и эпюры вычерчиваются в выбранном масштабе на миллиметровой бумаге с обязательным указанием всех необходимых размеров и обозначений.