ТЕОДОЛИТНЫХ И НИВЕЛИРНЫХ ХОДОВ

229. Уравнять систему теодолитных ходов с одной узловой точкой
(табл. 72) и составить схему ходов. Для первого варианта дан чертеж
на рис. 33.

 

 

 

 

 

 

230. Вычислить и уравнять высоты точек системы нивелирных ходов с одной узловой точкой по данным нивелирования IV класса, приведенным в табл. 73, рис. 34.

Пример решения задачи (вариант 16) приведен в табл. 74 (рис..35).

Вычисление в е р о я т н е й ш е г о значения от-f( й т к п vsitotnrn rrvHKTa

Средняя квадратическая ошибка единицы веса

где п — числобходов в системе;

_{fX =} |/i^₌₌23,9 мм.

Средняя квадратическая ошибка нивелирования на 1 км ходе

и ■ 23,9 г, я

т = —~, т ±= —т= = 7,6 мм.

Заметим, что₄ если вес вычисл яется по ф ормуле р — с/п, где га — число штативов в ходе, т = ц/с]/ [ra]/[L].

ее

 

 

 

 

 

 

231. Произвести уравнивание нивелирной сети IV класса спосо­бом полигонов проф. Попова (во всех вариантах, указанных в табл. 76, за исходные отметки принимать отметки, указанные на рис. 36).

Пример решения (вариант 1, рис. 37).

1. Между исходными пунктами пунктиром обозначают условный
ход 1Р2. По этому ходу превышение равно разности твердых отметок
h_lt2 = —5,522 м. Оно изменению не подлежит; чтобы это обеспе­
чить, длину хода условно принимают равной нулю.

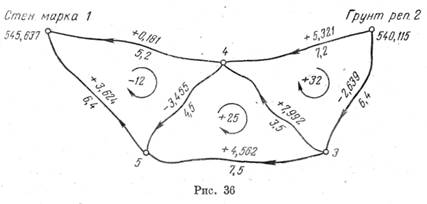
2. В каждом полигоне по ходу часовой стрелки вычисляют не­вязку в превышениях по формуле f_h — 2 /j. Убедившись в ее допусти­мости, невязку вписывают внутри заготовленной таблички (очерчен­ной жирными линиями). Длину каждого хода обводят кружком.

3. Вычисляют красные числа для каждого полигона по формуле L_t!P, где L_t — длина хода, Р -- периметр соответствующего

Таблица 75

 

 

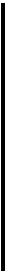в жирную рамочку и распределяют по ходам. Во втором полигоне вторичная поправка хода 4—3 равна +1,- а ход 5—4 получил по­правку в первом круге —1. Таким образом, невязки в полигоне нет; (+1) + (—1) = 0. В /77 полигоне поправка хода 1—4 (—3) дает невязку —3, которую аналогично первому полигону распределяют по ходам. В IV полигоне невязки нет; ходы 2 — 4 и 4 — X получили вторичные поправки соответственно +1 и —1, сумма которых равна 0.

Переходят к третьему кругу распределения невязок. Осталась неучтенной лишь поправка в ходе 5 — 4 во II полигоне, равная —1. Невязку полигона —1 распределяют на ход 3 — 5_t красное число которого (0,49) наибольшее в данном полигоне.

5. Находят окончательные значения поправок. Подсчитывают
алгебраическую сумму поправок в каждой табличке. Для внешних
ходов эти суммы, взятые с обратным знаком, будут окончательными
поправками. Их выписывают в скобках внутри полигонов: в первом
полигоне (—13), во втором (—14), в третьем (+2). Для каждого
общего хода двух смежных полигонов имеются по две таблички,
расположенные по разные стороны хода. Так, для хода 3—4 в та- /
бличке внутри полигона / поправка +7, для хода 4 — 3 в табличке
внутри полигона II поправка также +7. Последнюю величину
переводят на ход 3 — 4 (в / полигон) с обратным знаком. Складывая

— 7 и —7, находят поправку хода 3 — 4. Она равна нулю. Действуя
в таком порядке, находят поправки остальных внутренних ходов.
Для хода 5—4 [—9 -f (—2)] = —И, для хода 4 — 5 (полигон ///)
[(+2) + (^9)] = +11 и т. д.

Контроль уравнивания: сумма поправок должна равняться не­вязке с обратным знаком. Например, в первом полигоне (—19) +

— (—13) + 0 = —32 невязка полигона равна +32.

6. Вычисляют уравненные значения отметок узловых точек

#з = 540,115 + [-2,639 + (-13)] = 537,463,

#4 = 537,463 + [+7,992 + (0)1 = 545,455,

Я₅ = 545,455 + [-3,455 + (+11)] = 542,011

п для контроля получают отметку стенной марки 1

#_х^= 542,011 + [ +3,624 + (+ 2)] = 545,637 м.

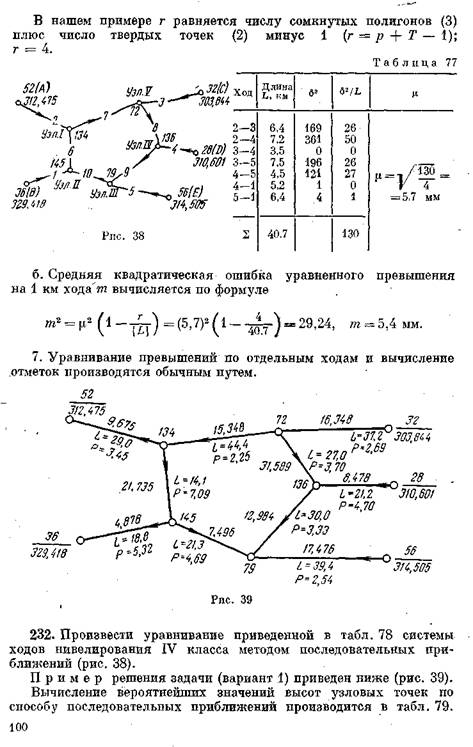
а. Средняя квадратическая ошибка измеренного превышения
на 1 км нивелирного хода \х (ошибка единицы веса) вычис­
ляется (табл. 77) по формуле

где р — вес, равный 1/L; а б — ошибка превышения в ходе (звене), равная по абсолютной величине поправке хода; подставив значение веса, получим

[*■-[■£!!

г + числе д#бав*чно измеренных величин.

7* 99

 

 

 

 

 

Во втором и п ос ледующих приближениях значения высот, записанные в строке 2, вычислены с учетом при­веденных весов. Например, высота реп. 145 во втором приближении получена следующим образом:

329,418 - 4,878 = 324,540,

302,803 - 21,735 = 324,538,

332,029-7,496 = 324,533,

40x0,31 + 38x0,42 + 33x0,27 = 37,

Я = 324,537.

В каждом приближении используются последние, полученные до этого значения высот смежных пунктов.

Вычисления продолжаются до тех пор, пока значения высоты одних и тех же узловых точек в двух последних приближениях будут одинаковыми в пределах точности вычислений, т. е. 1—2 еди­ниц последнего вычисляемого знака. Последнее из них является искомой уравненной отметкой пункта. Поправки v, которые следует ввести в измеренные превышения по каждой линии, равны разности между уравненной отметкой узловой точки и соответствующим значением высоты узловой точки, полученным в графе последнего приближения по данной линии.

Например, поправка превышения со стен. реп. 79 на грунт, реп. 145 (—7,496) равна 324,538 — 324,530 = +8. Поправка в обрат­ное превышение с реп. 145 на стен. реп. 79 равна 332,026 — 332,034 = = -8.

Контроль правильности вычисления:

к = [p^v]?g ± 0,5 мм для каждой узловой точки.

Оценка точности. Среднюю квадратическую ошибку единицы веса вычисляют по формуле

^r f z — и

где z — число линий; и — число узловых точек.

Средняя квадратическая ошибка нивелирования на 1 км- хода вычисляется по формуле

V-

т = _Г~.

Ус

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Глава XI ПОЛИГОНОМЕТРИЯ

МО. Обработать журнал измерения линии полигонометрии I раз- л квантовым геодезическим дальномером СМ-3 (КДГ-3) и вычислить дошит этой стороны, приведенной на плоскости в проекции Гаусса — Кзак-ера. Постоянная дальномера AD_r = —0,364. Результаты изме-зй даны в табл. 87. Шгаисления производить в две руки.

1ояснение. В результате обработки журнала находят ирвзонтальное проложение измеренной линии Z)„_CT. Например, при —енян варианта 8 D_mr = 189,950 м. Это расстояние редуцируют плоскость в проекции Гаусса — Крютера.

ченпе длины измеренной стороны полигонометрии, приведен­ие на плоскость в проекции Гаусса — Крюгера, вычисляется по

d = D_m+*, + *,■+& +6_h, (ХИЛ)

от ' — соответственно поправки за центрировку дальномера

ею отражателя. Поправки удобно вычислить при помощи таблиц для вычисления - хны сторон полпгонометрип и трплатерации 3 и 4 классов, изме-з радиодальномерами (Ю. Г. Бугаева, Ю. П. Гричука ж Б. Д. Ярового. Выписка нз этих таблиц, необходимая для реше­ны вариантов данной задачи, приводится в прилож. 1, 2.

-40 считается, что приборы точно сцентрированы во время намерении, поэтому не возникает необходимости введения вит] лровку и редукцию. Поправку

Он = -4гДист (^XIL2)

i для приведения длины стороны на уровень моря. Ее находят при помощи таблиц (прилож. 1) по формуле

б_я = —{К\ + К₂) Б_ИСТ.

Коэффициент K_t выбирают по аргументу Н_т. В данном варианте

„. 387,02 + 390,36 _QQQ „
#_m =------------- X--------- = 388,7 М.

/' Из таблиц К = 0,0596+ 0,0015 X 0,9 = 0,0610. По средней оциссе х_т = 3450, Н_т и азимуту А — 154° выбирают К₂ = 0,002, тогда

8_Н = -(0,0610 + 0,0002) 190 = -12 мм.

Поправку бь за приведение длины стороны на плоскость в проек­ции Гаусса вычисляют по формуле

6* 4*1+ *»)>««,

 

 

 

 

 

 

 

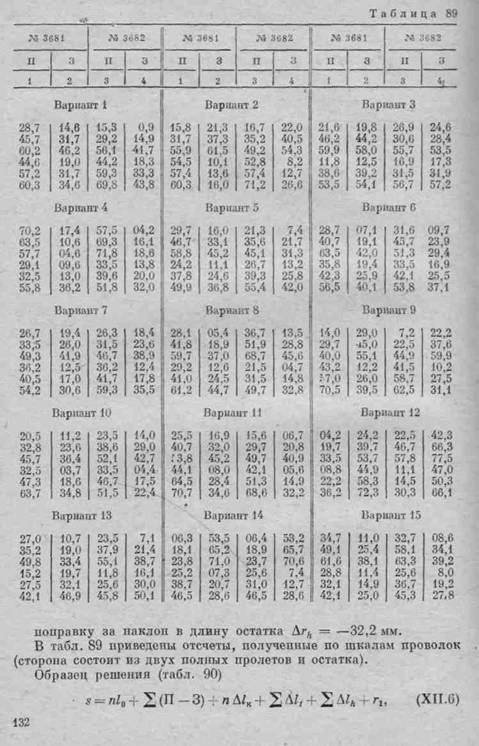
где п — число полных пролетов;

1₀ — номинальная длина проволоки; (П — 3) — разность отсчетов по передней и задней шкалам про­волоки.

243^Вычислить длину стороны d_x_ ₂ хода полигонометрии II раз­ряда",' определенную параллактическим методом (рис. 65).

Условия задания. Со створной точки С намечены точки В₁ и В ₂ — концы базиса Ъ, расположенного перпендикулярно к опре­деляемой линии 1 — 2. Расстояния В_ХС и СВ₂ не равны между собой.

Базис Ъ измерен стальной рулеткой (лентой), уравнение которой 1 = 10 м + 0,4 мм + 0,125 (t — t₀), мм, t₀ = 20° С.

1йЗ

 

 

 

 

 

 

Продолжение табл. 94

244. Для привязки настенных полигонометрических знаков с пункта полигонометрии I разряда К до них измерены расстояния н горизонтальные направления (рис. 66, табл. 93). Вычислить коор­динаты стенных пунктов и произвести контроль их определения. Исходными данными являются: х_к = +4045,225 м,

Пояснение к решению.

1. Находят горизонтальные проложенйя линий местности. Для
этого из измеренных значений расстояний вычитают поправки за
наклон, вычисляемые по формуле А_л = h²/2D. Превышения между
определяемыми пунктами получают как разность соответствующих
превышений между ними и исходным пунктом, например:

ч

2. Вычисляют дирекционные углы, для чего к исходному дирек-
ционному углу прибавляют измеренные направления.

3. Вычисляют приращения координат и по ним — координаты
определяемых пунктов.

4. Решением обратной геодезической задачи вычисляют рассто­
яния между пунктами 1, 2 ж 3.

По разностям вычисленных и измеренных значений расстояний находят их относительные ошибки. Они не должны превышать точность полигонометрии II разряда — 1: 5000.

245. Вычислить координаты пунктов полигонометрического хода
I разряда и составить схему хода по следующим данным (табл. 94,
рис. 67).

Глава XII ТРИАНГУЛЯЦИЯ

ПОВЕРКИ И ИССЛЕДОВАНИЯ ТЕОДОЛИТОВ

246. Для определения правильности хода фокусирующей линзы
зрительной трубы теодолита ОТ-02М наблюдались 2 точки, рас­
положенные по одному направлению на разном удалении от инстру­
мента. -___^^

Получены следующие средние отсчеты:

КЛ= 63° 28'06" КЛ= 62° 59'52" КП = 243 28 25 КП = 243 00 02

Сделать анализ хода фокусирующей линзы.

247. Описать подробно, как устранить коллимационную ошибку
у теодолита ОТ-02, если полученные при поверке отсчеты по гори­
зонтальному кругу равны: 1) КЛ = 45°
26' 38^s и КП = 225° 28' 02^.

248. При поверке перпендикуляр­
ности оси вращения трубы к основной
оси вращения инструмента определен
угол наклона 6 оси вращения трубы, t
При этом получены (рис. 68): расстоя­
ние между проекциями точки А на стене
В — 6 мм, угол наклона линии визирова­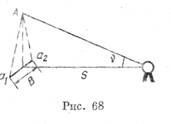
ния на точке A v = 22°, горизонтальное расстояние от теодолита
до стены s = 25 м. Вычислить значение угла наклона б и указать
допуск, определенный инструкцией.

Решение:

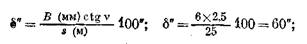
допускается 5".

249. Решить предыдущую задачу при условии, что 5 = 4 мм,
v = +29°, s = 30 м.

250. Описать подробно, как приводится к нулю Mz, если отсчеты
по вертикальному кругу теодолита ОТ-02м

КП = 90° 37' 24", КЛ = 89° 25' 36".

251. Решить предыдущую задачу, если отсчеты взяты по вер­
тикальному кругу ОТ-02 КП = 88° 56' 32^, КЛ = 91° 04' 20®.

252. Для исследования систематических ошибок оптического мик­
рометра теодолита ОТ-02М необходимо изготовить марку — на­
чертить на бумаге две параллельные линии. Рассчитать рассто­
яние t между отрезками, если расстояние s от теодолита до марки
20,6 м. При расчете воспользоваться формулой

as

где в качестве а принять угол, укладывающийся 5 раз в пределах шкалы оптического микрометра.

253. По данным исследования правильности вращения алидады
оптического теодолита (табл. 95) построить график изменений вели­
чин v, характеризующих эксцентриситет алидады, и провести от

руки плавную кривую типа синусоиды (рис. 69). 'Какие допуски предусмотрены инструкцией и соответствуют ли им результаты данного исследования?

Таблица 95

Примечание. Ломаную на графике прямого хода вычерчи­вают сплошной линией, обратного — пунктирной линией.

254. Определить допустимость 2F максимального значения коле­
баний величин v, вызываемых влиянием эксцентриситета лимба

при наиболее невыгодной его ориентировке, если получены: угловой элемент эксцентриситета алидады Р = 19° (см. рис. 69) и наибольшая ошибка в отсчете за эксцентриситет алидады / = 16" (выбранные из графика v) и соответствующие параметры Р_х == 62° и /_х = 6", выбранные из графика величин v_t, построенного при исследовании эксцентриситета лимба (он здесь не приводится). Решение.

Р - Р_х = (19° + 360^?) - 62° = 317°.

По элементам f_x (Р — Р_г) или [360 — (Р — PJ] и f_x строим (рис. 70) треугольник АЛД (масштаб в Змм — 1"); из него опре­деляем /₂ = 12",

^ = /_{1 +} /₂ = б" + 12" = 18", 2F = 36".

Допустимо 40".

255 Решить предыдущую задачу по следующим данным:

а) Р = 37°, Рг = 110°, /=12", Д =10";

б) Р = 216°, Р_х = 98⁰, / = 9", /!=15",

256. Вычислить поправку за рен А?- в отсчет а по оптическому
микрометру, если рен оптического микрометра ОТ-02М г = +1,8"
и отсчет а = 3' 22".

Решение.

Аг — —г- а,

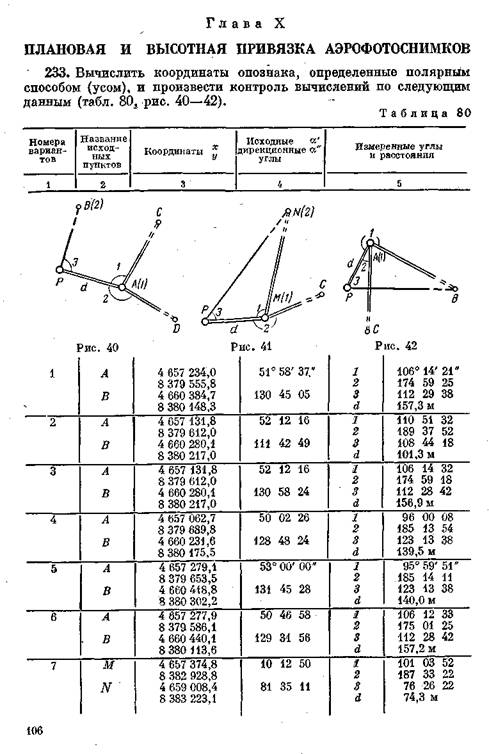
I -

Т где i — цена деления лимба;

Аг = -^202"=+1,2".

257. Составить таблицу поправок за рен на всю шкалу оптиче­ского микрометра ОТ-02М для отсчетов, кратных 10", если рен г = +2,1".

258. Подсчитать, насколько можно ошибиться в подсчете 2с = = КЛ — (КП ± 180°), если зенитные расстояния направлений отличаются от 90° на 5° и наибольшее допустимое значение 2с равно 20". Ошибка в отсчете, вызываемая коллимационной ошибкой с,

sin z

259. При наблюдении горизонтальных направлений на пункте
величина 2с во всех приемах по направлению на пункт А колеблется
от —2" до —5", а по направлению на пункт В — от +9" до +12".
Это вызывает большие колебания величин 2с в-приеме. Определить
степень влияния на значение 2с ошибок, вызываемых наклоном оси
вращения трубы при следующих условиях: зенитное расстояние
по направлению на пункт A z_A = 85° 2', на пункт Bz_B = 94° 58',
угол наклона оси вращения трубы б = 30".

Для решения следует воспользоваться формулой 2с = КЛ —КП ± 180° - —.

tgz

»

260. При наблюдении оптическим теодолитом направления, зе­
нитное расстояние которого z = 95° 15', взяты отсчеты по уровню:
при КП отсчет по левому концу пузырька л_х = ±3,8, по правому —
Hj = —5_l54; при КЛ л₂ = +3,5 и п₂■= —5,0. При отсчитывании
принято, что нуль уровня расположен посередине (такое положение
можно условно принять при любом виде подписей делений уровня).-

Цена деления уровня т = 7,0". Вычислить поправку А в направ­ление за наклон вертикальной оси вращения инструмента и значение нульпункта уровня х. Решение.

A = 6ctgz-|-,

где b — наклон горизонтальной оси в делениях уровня равен

_{ъ =} (д_г + П1) + (Лд + п_а) ^ (3,8-5,4)+ (3,5-5,0) ₌ _- _{ ^

Из таблиц поправок А_г (см. инструкцию *) по аргументам z = = 95° 15' и Ъ = —1,6д выбирают А, для т/2 = 1". Знак A_t, завися­щий от знаков сомножителей Ъ и ctg z, будет плюс: А, = +0,15, А" = А_г (т"/2) = 0,15 X 3,5" = +0,5";

261. С точки О измер ен уго л р между направлениями на пункты А
и В z_A = 84° 30', zb == 93° 50'. Определить значение поправки за
наклон оси вращения инструмента в измеренный угол, полученный
как разность направлений ОБ и О А, и для контроля постоянства
нульпункта х его значение.

В табл. 96 даны те же обозначения, что и в задаче 260. Цена деления уровня т = 6,6".

262. Даны отсчеты по оптическому микрометру, полученные
в одном приеме при исследовании систематических ошибок измерения
углов, вызываемых наличием люфта подъемных винтов (теодолит
ОТ-02М). Определить среднее значение условного угла.
Круглево Кругправо

1.34,2" 34,5" 3.23,8" 23,4"

после вращения алидады после вращения алидады

* Инструкция о построении государственной геодезической сети СССР, М., «Недра», 1966, прилож. 22, табл. 5.

по ходу часовой стрелки против хода часовой стрелки

2.34,1" 33,9" 4.23,9" 24,5"

Обработку приема вести по образцу, данному в учебнике по выс­шей геодезии авторов В. Л. Ассура, М. Н. Кутузова и М. М. Мура-вина (табл. 9). Ответ: систематическая ошибка равна —0,5".

СОСТАВЛЕНИЕ ПРОЕКТА ТРИАНГУЛЯЦИИ ОЦЕНКА КАЧЕСТВА ЕЕ ГЕОМЕТРИЧЕСКОГО ПОСТРОЕНИЯ

263. Определить наличие видимости между проектируемыми пунк­тами А и В. При отсутствии видимости рассчитать высоты сигналов, которые должны быть построены на этих пунктах, и, в частности, рассмотреть возможность постройки сигнала только на одном из них.

Считать, что препятствие находится в точке С. Для решения задания с карты выбраны величины: высоты точек Н_А, Н_в и Н_с и расстояния s_x между точками А и С и s₂ — между точками В и С (табл. 97).

Таблица 97

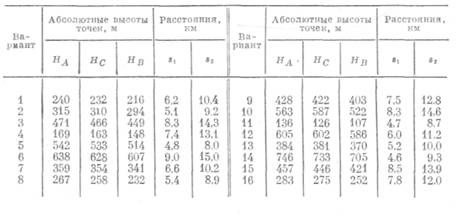
Решение. Расчет высот сигналов можно произвести как гра­фически, так и аналитически (что точнее). Обычно применяется формула В. Н. Шишкина. Ниже предлагается способ решения за­дачи, при котором одновременно определяют наличие видимости между проектируемыми пунктами и, если ее нет, рассчитывают вы­соты знаков.

1. Вычисляют величину Н_Свнч

Видимость между точками А и В будет при условии, что вы­бранное с карты Н_с <Я_Сеыч.

2. Если видимости нет, сразу получают высоты сигналов

10 заказ 121 145

В случае когда можно обойтись одним небольшим сигналом (его намечают на ближайшем к препятствию пункте), высоту сигнала вычисляют по формуле

1 ~ \ С О_ВЫч) _S2

Вычисления удобно производить при помощи логарифмической линейки. Поправки за кривизну Земли и рефракции v выбирают из таблиц или вычисляют по приближенной формуле

S2 (КМ)

Приведем решение первого варианта (табл. 98).

Таблица 98

Н_с = 232 м больше Н_Свыч = 226,8 м. Видимости нет. Если принять вариант, при котором на пупктах А и В высоты знаков одинаковы, то

г_{1 =} г₂=я_г—я_с =5,2 м.

Если остановиться на постройке только одного сигнала^ на пункте А (он ближе к препятствию), то

h = 5,2 -Н§- = 8,3 м.

Окончательный вариант высот пары знаков находят путем под­бора выгоднейших их значений (используя правило коромысла) с учетом ряда дополнительных факторов, в том числе дальности доставки стройматериалов на пункты. Все это связано с дополни­тельными условиями, которые в данном примере не задаются.

264. В запроектированном ряде триангуляции (см. рис. 71) пред-вычислить обратный вес логарифма стороны HJ, среднюю квадра-тическую ошибку логарифма этой стороны и ее относительную ошибку.

 

где 434 294 — значение модуля натуральных логарифмов, выражен­ное в единицах 6-го знака логарифмов.

Таблица

265. На листе карты масштаба 1: 50 000 У-34-37-В (Снов) соста­
вить схему проекта триангуляции 3 и 4 классов для обоснования
топографической съемки в масштабе 1: 5000 на территории, охва­
ченной трапециями У-34-37-В-а-4, У-34-37-В-6-3, У-34-37-В-В-2 и
У-34-37-В-2-1. В качестве исходных даются сторона триангуляции
2 класса Долгая (8007) — Зеленая (8016) и пункт 2 класса Федо-
ровка (6409).

При необходимости постройки сигналов приложить расчет их высот, считая, что строительный лес можно доставить из леса южнее села Лебяжье (см. карту У-34-37-В).

266. Рассчитать высоты знаков на пунктах А и В, если Н_А —
= 523 м, Н_в = 518 м, препятствие в точке С Н_с = 516 м, к которой
надо прибавить высоту растущего там леса, равную 18 м. Расстояние
до препятствия sac = 5,2 км и s_CB = 10,4 км.

Указание. Расчет вести по формулам В. Н. Шишкина согласно образцу, приведенному в учебнике по высшей геодезии авторов В. П. Ассура, М. Н. Кутузова, М. М. Муравина, используя нри этом формулу

Hi = h_t + v_t + а,

где H_t — высота знака, h_{ — превышение препятствия над пунктом i, а — высота луча над препятствием; в триангуляции 1 класса в зави­симости от района работ она должна быть от 2 до 6 м, в триангуляции 2—4 классов условно принимается равной 1—2 м.

ИЗМЕРЕНИЕ ГОРИЗОНТАЛЬНЫХ УГЛОВ, НАПРАВЛЕНИЙ И ЗЕНИТНЫХ РАССТОЯНИЙ

267. Обработать страницу журнала измерения горизонтальных
направлений способом круговых приемов, выполненного теодолитом
ОТ-02М (табл. 101).

 

 

268. Обработать страницы журнала измерения горизонтальных
углов способом Шрейбера, выполненного теодолитом ОТ-02М
(табл. 102).

269. Обработать страницу журнала измерения зенитных рассто­яний теодолитом ОТ-02 (табл. 103).

270. Для аналитического определения высоты верхнего основа­ния визирного цилиндра над центром пункта измерены (рис. 72):

d₂ — расстояние от теодолита

(точка 0) до центра С; v_x — угол наклона направления на верх визирного цилиндра; ^2 — угол наклона направления на верх вехи (визира над центром); ev₀ — отрезок на центрировочном листе, являющийся проек­цией линейного элемента редукции на дополнительно прочерченное направление СО. Определить высоту знака, если радиус основания визирного ци­линдра (для всех вариантов) г — — 15 см (табл. 104). Решение:

v₁=+24?05', v₂=+6°30',

dj = 14,81м, d_s—15,00 ж, а = 2м.

Z=J₁tgv₁-d₂tgv₂-fa, J = +6,62 —(+ 1,71) + 2,00 = 6,91 м.

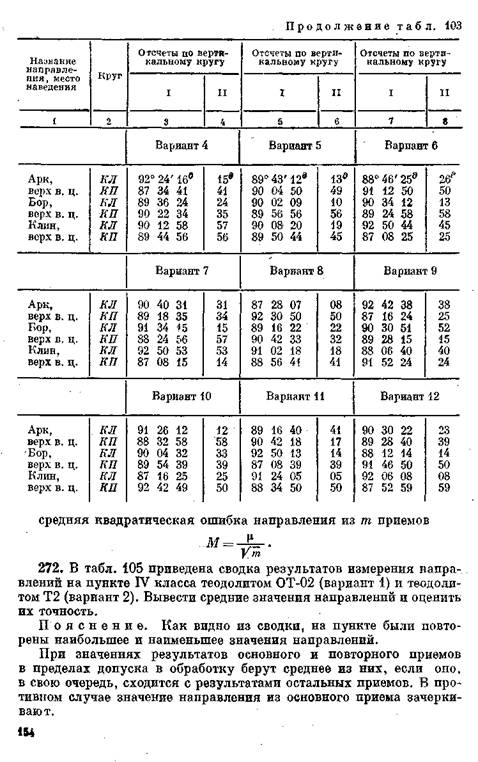
271. Оценить точность измерения горизонтальных направлений
способом круговых приемов по сходимости результатов на пункте.
Получены суммы уклонений v измеренных направлений во всех
приемах от вычисленных по ним средних значений:

число приемов т = 12; число направлений п = 3.

Формулы для оценки точности:

средняя квадратическая ошибка направления из 1 приема

^{ГДе к =}/7^ГГТ); Для ^{12 п}Р^ие^^{0В к} = °№

 

 

 

 

 

 

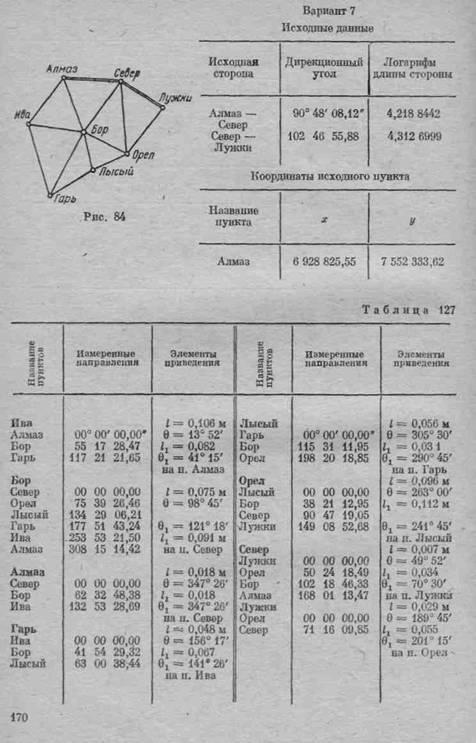
отмечающие следы проектирующих плоскостей, проходящих через ось визирного цилиндра, центр пункта и ось инструмента. Одно­временно даны магнитные азимуты всех направлений, проводимых с проекций оси визирного цилиндра У и оси инструмента /.

При помощи восковки требуется перенести рис. 73 (74) на белый лист бумаги, восстановить содержание центрировочного листа, измерить и подписать значения линейных I (1_г) и угловых 0 (9_X)

элементов центрировки и редукции, пользуясь образцом, приведен­ным в учебнике или в инструкции.

Вариант 1 (см. рис. 73)

Магнитные азимуты направлений, проводимых с точки У: 1) на пункт А - 95° 00'; 2) на пункт В - 336° 30'.

Магнитные азимуты направлений, проведенных с точки i J: 1 на пункт А — 95° 30', 2) на ориентирный пункт № 1 — 11» 30; 6) на пункт В — 337° 30', 4) на ориентирный пункт № 2 — 357; Вариант 2 (см. рис. 74)

Магнитные азимуты направлений, проводимых с точки У: 1) на пункт А - 154° 00', 2) на пункт В - 318° 30'.

Магнитные азимуты направлений, проводимых с точки J: 1) на пункт А «= 155° 00', 2) на пункт В - 320° 00'; 3) на ориентирный пункт № 1 — 8° 30' 4) на ориентирный пункт № 2 — 7b UU.

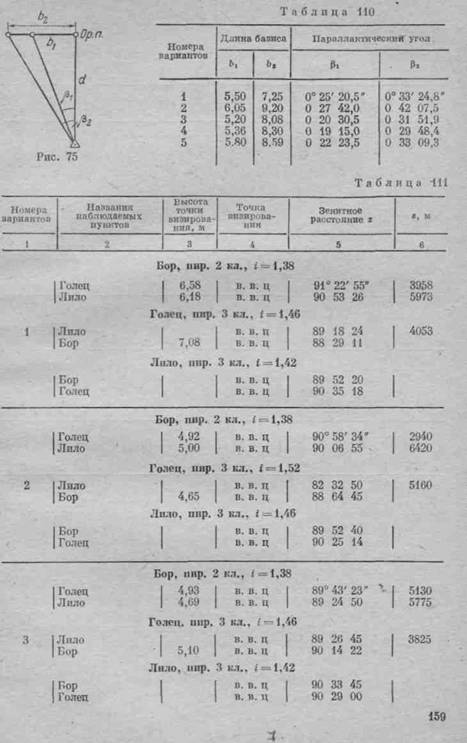
278. Для определения расстояния до ориентирного пункта Op. n на нем измерены 2 коротких базиса Ъ_х и Ъ_г (рис. 75), расположенных перпендикулярно к направлению на центр триангуляционного пункта, и с последнего измерены высокоточным теодолитом соответ­ствующие параллактические углы Pi и р₂-

Получено: Ъ_г = 5,00 м, Ь₂ = 7,00 м; р\ =.0 27 22,2, р₂-

= 0° 38' 19,0".

Вычислить среднее расстояние d до ориентирного пункта

(табл. 110).

279 Вычислить превышения, полученные методом тригонометри­ческого нивелирования по сторонам треугольника, по следующим данным (табл. 111). 158

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Продолжение табл. 134

СОСТАВЛЕНИЕ ИНФОРМАЦИИ ДЛЯ, УРАВНИВАНИЯ ВЫСОТ ПУНКТОВ НА ЭЦВМ «М-20»

293. В задаче 292 приводятся результаты геодезического нивели­рования по сторонам триангуляционных сетей.

Составить информацию для уравнивания высот пунктов этих сетей на ЭЦВМ М-20 по программе, предложенной Е. И. Добрыниной и С. Г. Морозковым.

Образец заполнения информации.

Общие сведения. Программа рассчитана на совместное уравнивание высот не более чем 200 пунктов при числе направлений на каждом из них, не превышающем 13. В результате уравнивания ЭЦВМ выдает отметки определяемых пунктов и их средние квадра-тические ошибки.

Высота пункта в каждом приближении H_t определяется как сред­нее весовое по формуле

H'_iPl + H]p₂+...
■Н i — ----------------- i------- i--------------- '

Л + -Р2+- • •

где р = 100/s².

Вычисления прекращаются тогда, когда расхождение между значениями отметок всех пунктов в последних двух приближениях не превышает заданной величины 0,05 м (допуск на конец уравни­вания).

Оценка точности окончательных результатов производится по следующим величинам:

а) средняя квадратическая ошибка определения отметки по од­
ному направлению (ошибка единицы веса)

_ -,/ [pw]

где п — число направлений на определяемом пункте; v — отклоне­ние значений полученной отметки по каждому направлению от ее средневесового значения;

б) средняя квадратическая ошибка уравненного (среднего весо­
вого) значения высоты каждого пункта относительно смежных
пунктов

ц

V[P) '

в) средняя ошибка уравненного значения высоты пу<