Теорема Пуассона: Если вер-ть р появл.события А в каждом испыт.при неогранич. возраст. числа испыт. n измен. т.о., что n*p=a=const,то вер-ть того,что нек. событие А появ. =k раз в n независ. испыт.наход.по формуле 
.
Док-во: По формуле Бернулли вер-ть того, что событие А появ. ровно k раз в n независ. испыт.
Переходим к пределу:
Замечание. Теоремой Пуассона удобно пользоваться, если р→0, 
.
Теор.(Локальная т. Муавра-Лапласа). Если вер-ть появл. события А в каждом отдельном испыт. пост. и отлична от 0 и 1, т.е. 0<p<1, то вер-ть того, что событие А появ.= k раз в n незав. испытаниях. Наход. по формуле:
Где 
; q=1-p.
––плотность стандартного норм. распределения
Теорема(Интегр.т.Муавра-Лапласа). Если вер-ть появл. события А в каждом отдельном испыт. постоянна и отлична от 0 и 1, т.е.0<p<1, то вер-ть того, что событие А появ. от k1 до k2 раз в n независ. испыт. опред. по формуле:
, где 
—ф-ия Лапласа, где
, 
, 
.
Замечание. Функция Лапласа явл. нечет. ф-цией, т.е. Ф(-х)=-Ф(х), при х≥5, Ф(х)=0,5.
7. Математическим ожиданием дискретной случайной величины называют сумму произведений всех ее возможных значений на их вероятности. Обозначают математическое ожидание случайной величины Х через MX или М(Х). Если случайная величина Х принимает конечное число значений, то 
Если случайная величина Х принимает счетное число значений, то 
, причем математическое ожидание существует, если ряд в правой части равенства сходится абсолютно.
Замечание! Мат.ожидание дискретной случ. величины есть некоторое число и не явл.случ.величиной.
Свойства математического ожидания:
1) Математическое ожидание постоянной величины равно самой постоянной: М(С)=С
Будем рассматривать постоянную С как дискретную случайную величину, которая принимает одно возможное значение С с вероятностью 1. Следовательно,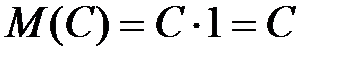 
. 
Замечание! Произведение пост. вел. Сна дискретн.
с.в. Х опр. как случ. дискретная вел. СХ, возм. знач. которой равны произв-ям постоянной С на возможн. знач. Х, а вер-ти возможн. знач. с.в. СХ равны вер-тям соотв-щих возможных знач. с.в. Х.
2) Постоянный множитель можно выносить за знак математического ожидания: M(CX)=CM(X).
Математическое ожидание случайной величины СХ 
3) Математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий: 
Следствие: Мат.эжиданиепроизведения любого конечного числа взаимно независимых случ.величин= произведению их мат.ожиданий.
4) Математическое ожидание суммы двух случайных величин рано сумме математических ожиданий слагаемых: 
Следствие: мат.ожидание суммы конечного числа случ.величин=сумме мат.ожиданий слогаемых.
Теорема1:
Математическое ожидание числа появлений события А в n независимых испытаниях равно произведению числа испытаний на вероятность появления события в каждом испытании: 
.
Доказ.:
Будем рассматривать в качестве случайной величины Х число появлений события А в n независимых испытаниях. Очевидно, общее число Х появлений события А в этих испытаниях складывается из чисел появлений события в отдельных испытаниях. Поэтому если Х1—число появлений события в первом испытании, Х2—во втором,…, Хn—в n-ом, то общее число появлений события 
. По свойству 4: 
;
Т.к.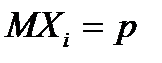 
,то
Таким образом, получим 
.
8. Дисперсией случайной величины Х называется число: 
. Дисперсия является мерой разброса значений случайной величины вокруг ее математического ожидания.
Средним квадратическим отклонением случайной величины Х называется число 
.
Формула для подсчёта дисперсии:
Свойства дисперсии:
1) Дисперсия постоянной величины С равна 0. DC=0.
2) Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат:
3) Дисперсия суммы двух независимых случайных величин равна сумме дисперсий этих величин:
Следствие: дисперсия суммы конечного числа независимыхслуч. величин=сумме дисперсий этих величин.
Теорема 2. Дисперсия числа появлений события А в n независимых испытаниях, в каждом из которых вероятность р появления события постоянна, равна произведению числа испытаний на вероятность появления и непоявления события в одном испытании: 
.
Доказ.: Обозначим через Х число появлений соб.А в n независимых испытаниях; Хi—число наступления соб.в i-ом испытании. 
Поскольку Xi–независимы др.от др., то 
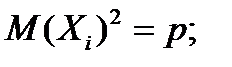
Т.к 
где q=1-p; Тогда
Начальным моментом порядка к случайным величинам Х называют математическое ожидание случайной величины 
:
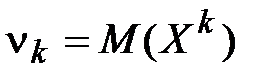. В частности, 
, 
.
Пользуясь этими моментами, формулу для вычисления дисперсии 
можно записать так: 
.
Центральным моментом порядка k случайной величины Х называют математическое ожидание величины (Х-МХ)^k.
. В частности
, 
. Следовательно,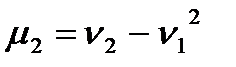 
.
