Элементы комбинаторики.
Основные правила комбинаторики:
Лемма1. Из m элем-ов а1,…,аm 1-ой группы и n элем-ов b1,…,bn 2-ой группы можно сост. ровно m∙n упорядоч. пар вида (аi, bj), содержащих по одному элем. из каждой группы.
Док-во:
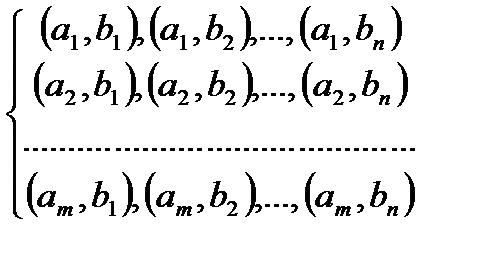
Лемма 2. Из n1 элем.1-ой группы a1, а2,…, аn1,n2 элем. 2-ой группы b1, b2,…, bn2, n k(индекс) элем. k-ой группы x1, x2,…, x n(индекс) k(индекс) можно сост. ровно n1∙ n2∙…∙nk различ. упорядоч. комбинаций вида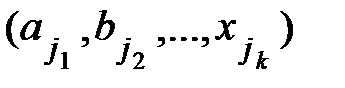 
, содержащих по одному элем. из каждой группы.
Число выборки. Пусть имеется множество, состоящее из n элементов {а1,..,аn}. Будем рассматривать выборку объёма k (aj1,..,ajk) из этих n элементов. Все выборки можно классиф. по 2 признакам:
1) упорядоченные и неупорядоченные.
2) с возвращением и без возращения.
Если выборка упоряд., то выборки с одним и тем же составом выбр. элем., но разным порядком элем. в выборках, считаются различными. Если выборка считается неупорядоченной, то все выборки с одним и тем же составом элем. отождествляются.
Таблица общего числа выборок объема k из n-элементов:
Упорядоч. выборка без возвращения наз. размещением. Число размещений из n по k:
.
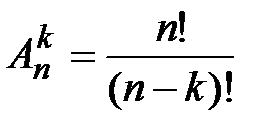Перестоновкой из k эл-ов- наз. совок-ть этих же эл-ов, записанных в произв. порядке.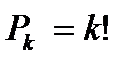 
Произвольное k элементное подмножество множества, состоящего из n эл-ов наз. Сочетанием из n эл-ов по k эл-ов.
Св-ва сочетаний:
1. 
.
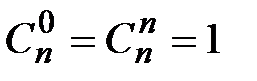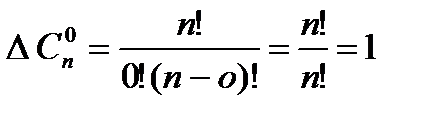
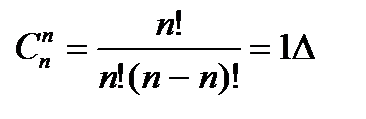
2. 
.
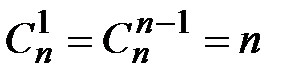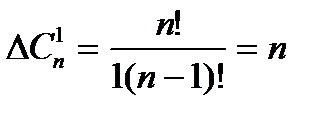
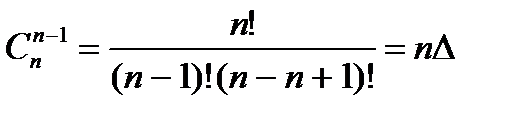
3. 
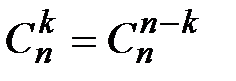. 4. 
.
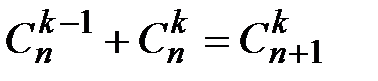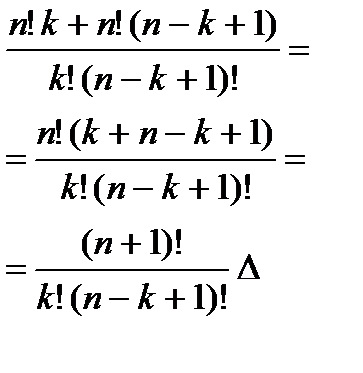
2.Свойства вероятности.
1. Вер-ть невозможного события=0, т.е. P(Ø)=0.
2. Вер-ть достоверного события равна =1, т.е. Р(Ω)=1.
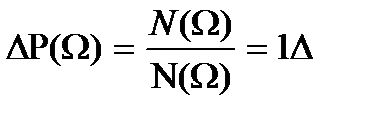
3. Вер-ть любого случ. события 0≤Р(А)≤1. ∆0≤N(A)≤N(Ω);
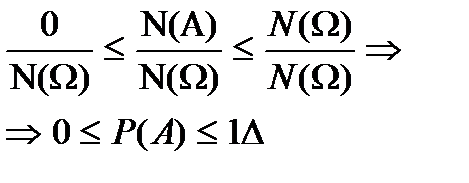
4. Обобщенная теорема сложения вер-тей.
5. Если события А и В несовместимы, то вер-ть их суммы =сумме вер-тей:
P(A+B)=P(A)+P(B)
6. (Теорема сложения k слагаемых). Если события А1, А2,…, Аk попарно несовместимы, то вер-ть их суммы=сумме вер-тей этих событий.
.
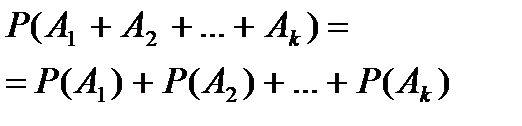7. Если событие А влечет событие В, то P(А)≤P(B).
.
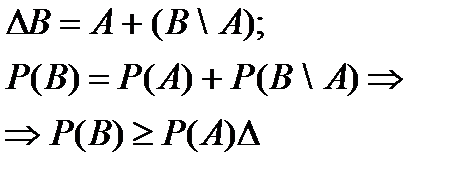8. Если событие А влечет событие В, то P(B\A)=P(B) - P(A).
9. Вер-ть события противоп. событию А находится как
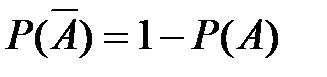
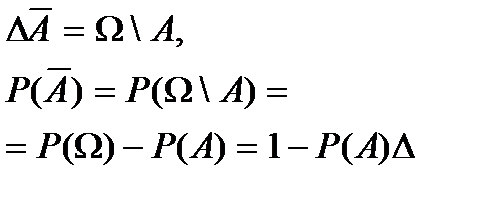
10. Если события Н1, Н2,…,Нk образ.полную группу, то сумма вер-тей этих событий=1.
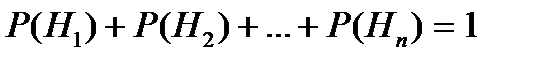
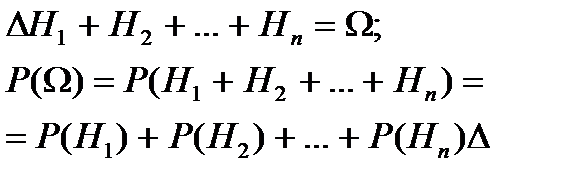
Условная вер-ть. Независимость.
Усл. вер-тью события B при усл. A наз. вер-ть события B, в предположении, что событие A наступило.
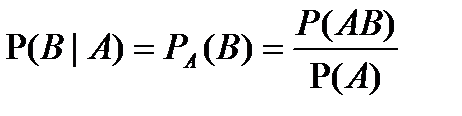
Теорема. (Умножение вероятностей): Вер-ть произведения 2ух событий равна произведению вер-ти одного из событий на вер-ть другого, при усл. первого.
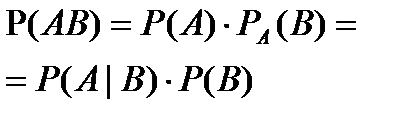
Теорема. (Обобщенная теорема умножения).
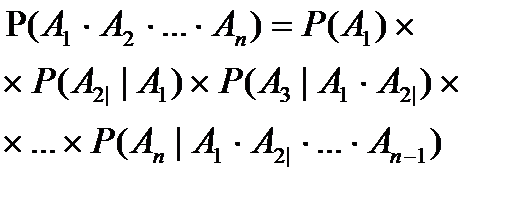
События А и В наз. независимыми, если вер-ть их произведения = произведению их вер-тей.
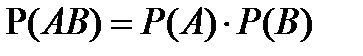
Теорема. События А и В независимы только тогда, когда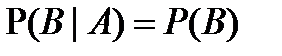 
.
События А1,А2,…,Аn наз. независимыми в совокуп., если выполн. след. усл.:
1) 
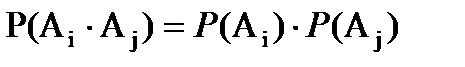(для i≠j; i,j 
{1,…,n}) – т.е. события попарно независ.;
2) 
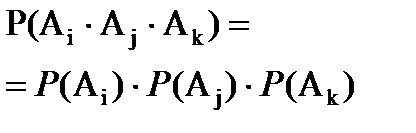
i≠j; j≠k; i,j,k 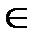{1,…,n} – т.е независимы по три;
…
n-1)
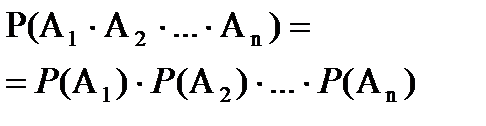
Можно сказать, что из попарной независимости еще не следует независимость в совокупности.
Формулы полной вероятности и Байеса.
Теорема 1. (Формула полной вероятности):
Если события Н1, Н2,…,Нn образуют полную группу, то вер-ть люб. события А, которое может совместно произойти с любым из событий, образующих полную группу, выч-ся по формуле:
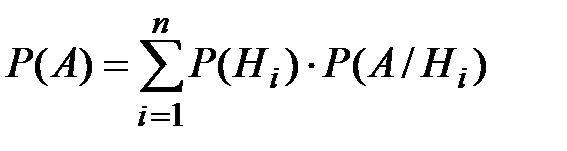
Док-во. Так как события
Н1, Н2,…,Нn образуют полную группу, то по опр.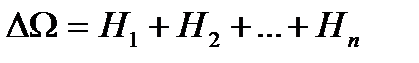 
. Умножим обе части этого рав-ва на соб. А 
.
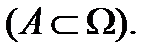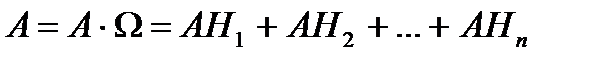
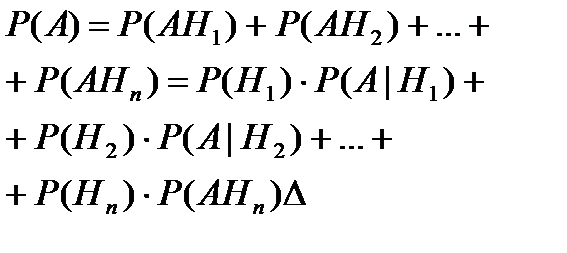Замечание. При примен. фор-лы полн. вер-ти, соб. (Н1, Н2,…,Нn), образ-щие полную группу – наз-ся гипотезами.
Теорема 2. (Формула Байеса): Пусть события Н1, Н2, …, Нn образ. полную группу, А – нек. событие, кот.может произойти совместно с люб. из событий, образ. полную группу, причем P(A)≠0, тогда условие вер-ти гипотез при соб. А считаются по фор-лам:
, 
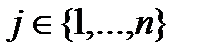
Док-во:
Замечание. При примен. формулы Байеса вер-ти
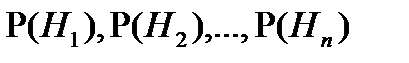- наз. априорными вер-ми гипотез, а вер-ти
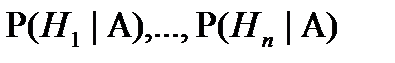- наз. апостериорными вер-ми гипотез.