2.5.1. ЭКВИВАЛЕНТНЫЙ ИСТОЧНИК ПИТАНИЯ – СИСТЕМА
В очень мощных системах напряжение можно принимать неизменными, а сопротивление системы принимается Х с=0. Для систем с конечной мощностью указываются ее параметры. В исходных данных для расчета задается реактивное сопротивление системы и ее мощность. Активное сопротивление системы можно определить как 
. Напряжение системы U с принимается равным U ср.н. – среднему номинальному напряжению соответствующей ступени (выбирается по ближайшему значению напряжения обмотки трансформатора к которой присоединена система). Среднее номинальное напряжение принимаются из следующих значений: 515; 340; 230; 154; 115; 37; 24; 20; 18; 15,75; 13,8; 10,5; 6,3; 3,15 кВ. Далее находится полное номинальное сопротивление системы по выражению:
(2.9)
затем Х с в именованных и относительных единицах в базисной системе единиц, при необходимости учитывается трансформация. В схеме замещения ЭДС системы принимают Е с= U с= U ср.н., далее выражают в относительных единицах в базисной системе, при наличии разделяющих трансформаторов, трансформируют.
2.5.2. ТРАНСФОРМАТОРЫИ АВТОТРАНСФОРМАТОРЫ
Двухобмоточные трансформаторы
В исходных данных для расчета приводятся мощности трансформаторов, напряжения обмоток, напряжение короткого замыкания. Полное сопротивление прямой последовательности двухобмоточного трансформатора в именованных единицах определяется по выражению
(2.10)
Реактивное сопротивление в именованных единицах определяется, используя напряжение короткого замыкания
(2.11)
т.к. обычно индуктивное сопротивление Х принимается численно равным U к [1].
Реактивное сопротивление в относительных единицах:
(2.12)
В формуле (2.10) Z н определяется относительно той обмотки для которой взято U н, при необходимости определения Z н относительно ступени напряжения расположенной за трансформатором, следует воспользоваться соответствующей формулой приведения (2.5) или (2.6). При нескольких ступенях трансформации использовать соответствующие формулы (2.8). Далее найденное сопротивление Х r выражается в относительных базисных единицах.
Активное сопротивление, сопротивление трансформатора r т можно найти по коэффициенту 
. Для трансформаторов значения 
в зависимости от мощности и высшего напряжения трансформатора (в виде графиков) приводятся в «Приложении» данного пособия. Активное сопротивление двухобмоточного трансформатора можно вычислить используя значение мощности потерь короткого замыкания, которые в зависимости от мощности трансформатора приводятся в [4]. Формула для расчета активного сопротивления:
(2.12)
где Р кз – мощность потерь к.з., кВт; S н – номинальная мощность трансформатора, МВ·А.
Реактивное сопротивление прямой последовательности двухобмоточного трансформатора можно определять по формуле:
(2.13)
Трехобмоточные трансформаторы (автотрансформаторы)
В расчетной схеме трехобмоточный трансформатор, автотрасформатор (АТ) представляют в виде трехлучевой звезды, при этом определяются сопротивления каждого луча звезды. Напряжение короткого замыкания для трехобмоточных трансформаторов (автотрансформаторов) задается для каждой пары обмоток при разомкнутой третьей, т.е. U кВС%; U кВН%; U кСН%. Все напряжения к.з., как правило, отнесены к номинальной мощности обмотки, мощность которой принята за номинальную мощность трансформатора (автотрансформатора). Напряжение к.з. луча звезды (обмотки) определяется по выражениям:
(2.14)
По известным U кВ%, U кС%, U кН% определяются сопротивления лучей расчетной схемы замещения по выражениям:
(2.15)
где U н – номинальное напряжение той ступени, для которой определяется сопротивления.
Индуктивные сопротивления Х принимаются численно равными U к, поэтому в некоторых литературных источниках выражения (2.14) могут быть записаны через сопротивления [1, 3 и др.]. После нахождения значений сопротивлений. их величины приводятся к расчетной ступени и выражаются в относительных единицах базисной системы. Активные сопротивления лучей в схеме замещения определяются с помощью коэффициента по графику, данному в «Приложении». Для определения мощности потерь по ветвям и дальнейшего расчета активных сопротивлений можно воспользоваться выражениями:
(2.16)
где индексы В, С, Н обозначают соответственно стороны высшего, среднего и низшего напряжений трансформатора. Предполагается, что напряжения к.з. и потери приведены к номинальной мощности трансформатора или АТ. Если для трехобмоточного трансформатора или АТ дается лишь одна величина потерь ΔР кт, то для каждого из трех обмоток принимают
(2.17)
Если же указано, что номинальная мощность одной из обмоток составляет 67% от S н трансформатора, то мощность потерь для этой обмотки будет равна [5]:
(2.18)
Трансформаторы с расщепленными обмотками
Трансформаторы с расщепленными обмотками характеризуются тем, что некоторые обмотки (низшего напряжения) выполняются из двух или более независимых обмоток для раздельного присоединения к секциям распределительного устройства. При расщеплении обмотки низшего напряжения на две, двухобмоточный трансформатор может рассматриваться как трехобмоточный с обмотками В, Н1, Н2 (см. табл.). Для трехфазных трансформаторов с расщепленной обмоткой НН на три части параметры определяются на основании заводских данных. Сопротивления трех лучей находят из следующих соотношений:
(2.19)
(2.20)
где параметры U кВН% и ΔР к соответствуют опыту к.з. при соединенных в параллель обмотках НН.
2.5.3. РЕАКТОРЫ
Если индуктивное сопротивление реактора Х р выражено в процентах. то в относительных единицах его значение
(2.21)
а перевод из относительных единиц в именованные по формуле:
(2.22)
где U нр- номинальное напряжение, кВ; S нр – номинальная мощность реактора. МВ·А; Х р может задаваться в Ом.
Активное сопротивление определяется по потерям активной мощности в фазе реактора ΔР н (кВт) и номинальному току I н (А):
(2.23)
Сдвоенные (расщепленные) реактора содержат две ветви с индуктивной связью между ними. Для них дается реактивное сопротивление одной ветви при отсутствии тока в другой Х р и коэффициент связи К р. В трехлучевой схеме замещения (см. табл.)
; 
(2.24)
Результирующее сопротивление реактора между зажимами при прохождении тока к.з. в одной ветви
; 
(2.25)
При прохождении номинального тока в обеих ветвях, реактивное сопротивление каждой ветви Х 12 = Х 13 = Х р(1-К р) [6].
Активные сопротивления соответственно равны
; 
. (2.26)
2.5.4. ЛИНИИ ЭЛЕКТРОПЕРЕДАЧ
Активное сопротивление воздушных линий определяется по формуле
(2.27)
Реактивное сопротивление прямой последовательности определяется по формуле
(2.28)
где r, X 1 – соответственно удельные (погонные) активное и реактивное сопротивления; l – длина линий.
Реактивное сопротивление линий обратной последовательности Х л2 равно сопротивлению прямой последовательности, т.е. Х л2= Х л1.
Удельное сопротивление нулевой последовательности линий (Ом/км) зависит от конструкции линий и для практических расчетов может быть взято из [1, 2].
Активное и индуктивное сопротивление прямой последовательности кабельных линий электропередач могут быть определены по (2.27) и (2.28). Реактивное сопротивление обратной последовательности равно реактивному сопротивлению прямой последовательности. Сопротивление нулевой последовательности зависит от конструкции кабеля, способа прокладки и т.д. Удельные значения сопротивлений могут быть взяты из [1, 2].
2.5.5. ОБОБЩЕННАЯ НАГРУЗКА
Обобщенной нагрузкой принято считать нагрузку, состоящую из освещений, различных электродвигателей, печей, конденсаторных установок, выпрямителей и т.п. Точный учет нагрузки, характеризующейся различным видом режимов ее работы и схем питания, представляет исключительно сложную задачу.
Влияние электродвигателей, составляющих обычно основную часть промышленной нагрузки. сводится к тому, что они в начале переходного периода при к.з. могут перейти из двигательного режима в генераторный, если ЭДС двигателей превосходит напряжение при к.з. на его зажимах. В связи с этим в инженерных расчетах ограничиваются приближенным учетом нагрузок. В схеме замещения нагрузка отражается сверхпереходной ЭДС 
, приложенной за сверхпереходным реактивным сопротивлением 
и активным сопротивлением r нг. Обычно принимают
; 
; 
.
Относительные значения в этих выражениях соответствуют рабочей мощности нагрузки и среднему номинальному напряжению. Пересчет реактивного сопротивления в размерные единицы (Ом) для напряжения U ср выполняется по формуле
(2.29)
где U ср – линейное напряжение. кВ; S нг – мощность нагрузки, МВ·А.
Сопротивление обратной последовательности для обобщенной нагрузки принимают таким же как для прямой последовательности для начального момента к.з.:
Х 2нг = 0,35
В схемах нулевой последовательности сопротивление обобщенной нагрузки определяется электрической сетью и условием включения нейтрали трансформатора.
2.5.6. ДВИГАТЕЛЬНАЯ НАГРУЗКА
Сверхпереходные ЭДС синхронных компенсаторов (СК) и синхронных двигателей (СД) работающих с перевозбуждением (Е ’’> U 0) находятся по одинаковым формулам (2.30) и (2.32):
(2.30)
где U *0, j *0, I *0 – соответствующие параметры предшествующего режима;
(2.31)
где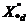 
- сверхпереходное сопротивление синхронной машины по продольной оси; Х *ВН – сопротивление внешнего элемента, отделяющего машину от шин с напряжением U *0. Допустимо использовать приближенное выражение:
(2.32)
При расчетах в размерных единицах формулы (2.31) и (2.32) будут справедливы без введения 
, если U 0 и E ’’ - фазные величины.
Для расчетов общего характера допустимо предшествующий режим считать номинальным:
Е ’’* = E ’’*(н); U *0 = U *н; I *0 = I *н; j 0 = j н (2.33)
При этом для СК sinj 0 = 1,0; а если другие данные отсутствуют то и для СД.
Для асинхронных двигателей и синхронных с недовозбуждением выражение (2.32) используется со знаком минус после U *0 (при Х *ВН = 0, Х ’’*dрез = Х ’’*d).
Для остальных параметров электрических двигателей можно принять следующее: U *н = 1, 
; при этом j 0 = j н = j, где j - угол определяемый в исходных данных.
Реактивное сопротивление Х ’’* = X *d(н) = X ’’*d, а если задана кратность пускового тока I п, то 
.
Полное сопротивление двигателей в размерных единицах определяется выражением: , если задано Р н, то
(2.34)
где h н – номинальный коэффициент полезного действия, который можно принять равным 0,90-0,95.
Для асинхронных двигателей активное сопротивление в омах можно определить по формуле
(2.35)
где M *п и I *п – кратности пускового момента и тока; P н и I н – номинальные: мощность в МВ·А и ток в кА. Номинальный ток двигателя I н можно определить по исходным данным используя выражение: 
.
Для АД активное сопротивление статора r 1 и приведенное к статору активное сопротивление ротора r 2 можно определить по формуле:
(2.36)
где h н – номинальный КПД.
Значение базисного активного сопротивления для синхронного двигателя можно получить следующим образом. Определяется отношение реактивного сопротивления к активному (сопротивления выражаются в относительных номинальных единицах) 
. Затем используя полученный коэффициент а определяется сопротивление в относительных базисных единицах: 
.
2.5.7. ГЕНЕРАТОРЫ
Для расчета параметров генераторов, которыми, как правило, являются синхронные машины, можно воспользоваться ранее приведенными выражениями. ЭДС определяется по выражению (2.32) используя исходные данные. Полная номинальная мощность S н по (2.34). Сопротивления как реактивное, так и активное находятся по выражениям, приведенным для синхронных двигателей. Если реактивное сопротивление задано в процентах, то для получения его значения в Ом используются следующие соотношения:
;
.
где U н – номинальное напряжение, кВ; S н – номинальная мощность. МВ·А.