Задачей поддержания требуемого режима СЭС является ограничение изменений параметров узловых точек системы в таких пределах, при которых сохраняется ее устойчивость, т.е. способность системы восстанавливать исходный или близкий к нему режим после его нарушения под воздействием различных возмущений [3]. Устойчивость системы определяется на основании расчета и анализа электромеханических переходных процессов учетом нормального, аварийного и после аварийного режимов, при этом рассматриваются существенные изменения режима и степень возмущающих воздействий.
К изменениям режима относятся отключение генерируемой и передаваемой мощностей, изменение частоты вращения генераторов и двигателей. Возмущающие воздействия разделяют на малые (слабые), при которых отклонения параметров режима от их установившихся значений несоизмеримо малы, и большие (сильные), вызывающие существенные отклонения параметров режима СЭС от номинальных значений.
В СЭС различают три группы электромеханических переходных процессов:
1. При малых отклонениях мощности и небольших изменениях частоты вращения;
2. При больших отклонениях мощности и малых изменениях частоты вращения;
3. При больших отклонениях мощности и больших изменениях частоты вращения.
К первой группе относятся нормальные переходные процессы, сопровождающие эксплуатационные режимы системы. Это процессы возникающие при включениях и отключениях генераторов, трансформаторов, линий электропередач, нагрузок и других элементов системы.
Исследования переходных процессов второй группы позволяют судить об устойчивости режима при больших возмущениях:
- КЗ в системе и последующие их отключения;
- изменения схемы соединения системы в результате отключения агрегатов станции или ЛЭП со значительными нагрузками;
- нормальное включение или отключение ЛЭП с большой зарядной мощностью;
- включение генераторов под действием самосинхронизации.
Исследование переходных процессов третьей группы позволяет определить, будет ли восстановлена синхронная работа части или всей системы после выпадения из синхронизма.
В практических расчетах устойчивости принимают ряд допущений:
- электромеханических процессы протекают при небольших изменениях частоты вращения синхронных машин (2-3 % синхронной частоты);
- напряжение и ток генераторов, а также ток возбуждения изменяются мгновенно;
- изменения режимов СЭС можно отразить в ее схеме, если ввести в нее новые значения ЭДС генераторов, мощностей, собственных и взаимных сопротивлений;
- несимметричные режимы можно привести к симметричным с помощью комплексной схемы замещения, считая что изменения движения ротора вызваны только моментами, создаваемыми токами прямой последовательности;
- изменения вызванные насыщением стали, можно не учитывать.
В процессе эксплуатации СЭС балансы мощности турбин и генераторов, электроприводов и нагрузок периодически нарушаются. Это происходит из-за несовпадения реального графика нагрузки с планируемым. С учетом принятых допущений уравнение баланса мощности для отдельного агрегата «турбина-генератор» в относительных единицах можно записать в виде
(4.1)
где Р т – мощность турбины, определяющая исходный установившийся режим системы (Р т = Р 0); Р эл – электромагнитная мощность генератора; Р пот – потери в агрегате; Р d – демпферный коэффициент; δ – угол, определяющий пространственное положение продольной оси ротора (угол между вектором ЭДС генератора и вектором U с напряжения системы); Т I – постоянная инерции вращающихся масс турбины и генератора.
Выражение (4.1) называется уравнением электромеханических переходных процессов и является основным определяющим работу агрегата.
Под устойчивостью СЭС понимают ее способность после случайных возмущений восстановить исходный или близкий к нему режим работы.
5. ЗАДАНИЕ 2. МЕТОДИЧЕСКИЕ УКАЗАНИЯ К РАСЧЕТУ ЭЛЕКТРОМЕХАНИЧЕСКИХ ПЕРЕХОДНЫХ ПРОЦЕССОВ
По заданию 2 необходимо привести текст задания, схему электрической системы [7, рис. 4], данные элементов схемы в соответствии со своим шифром (в виде таблицы). Далее составляется схема замещения системы, определяются базисные велечины. За базисную мощность целесообразно принять мощность первой электростанции, за базисное напряжение - напряжение нагрузки U б = U нг = 115 кВ. Затем рассчитываются коэффициенты трансформации и параметры элементов схемы замещения. В отличии от задания 1, активные сопротивления элементов, кроме нагрузки, определять не требуется.
Всем элементам исходной схемы замещения присваивается порядковый номер, параметры каждого элемента выражаются в относительных единицах и затем сводятся в таблицу.
Генератор G 1, в зависимости от решаемой задачи характеризуется теми или иными сопротивлениями Х *d(б), Х *q(б), Х ’*d(б), Х *2(б). Предварительно следует определить коэффициент приведения который удобно использовать при расчете выше указанных сопротивлений.
где Z н – полное номинальное сопротивление генератора G - 1; К 2Т1 и К 2Т2 возведенные в квадрат коэффициенты трансформаторов, соответственно первого и второго; Z б – базисное сопротивление.
Для нагрузки комплексное сопротивление в омах равно
После определения параметров всех элементов, схема замещения преобразуется к окончательному виду, изображенному на рис. 5.1.а (путем последовательного и параллельного сложения сопротивлений элементов). При определении Х э2 считать ЭДС генераторов G 1 и G 2 одинаковыми. Значения ЭДС Е э1 и Е э2 на этапе составления и преобразования схемы замещения определять не требуется.
Каждый раздел, пункт и подпункт задания и упражнения начинать с номера и наименования!
а
аfff 
б
в
Рис. 5.1.
5.1. ОПРЕДЕЛЕНИЕ ПРЕДЕЛА ПЕРЕДАВАЕМОЙ МОЩНОСТИ И КОЭФФИЦИЕНТА ЗАПАСА СТАТИЧЕСКОЙ УСТОЙЧИВОСТИ
5.1.1. ОПРЕДЕЛЕНИЕ ПРЕДЕЛА ПЕРЕДАВАЕМОЙ МОЩНОСТИ БЕЗ УЧЕТА ЯВНОПОЛЮСНОСТИ ГЕНЕРАТОРОВ ПЕРВОЙ СТАНЦИИ, ПРИ ОТСУТСТВИИ АРВ
Принимается Х d = X q и расчет ЭДС генератора G 1 осуществляется в соответствии с векторной диаграммой (рис. 5.1.б) по формуле
где Х dрез = Х d + Х вн, а Х вн – сопротивление участка «первая станция (G 1) – шины нагрузки» (U н = 1).
Предел передаваемой мощности
В приведенных формулах, как и в последующих, все величины выражены в относительных единицах. Соответствующие значки в обозначениях опущены с целью упрощения записей. Коэффициент запаса статической устойчивости определяется в процентах из соотношения
Расчет зависимостей Р пр и К пр от cos φ 0, пункт 1.1 «Заданий …» [7] следует свести в таблицу, содержащую значения cos φ 0 от 0,6 до 1,0 как для опережающих, так и для отстающих от напряжения токов. Таблица должна содержать значения промежуточных вычислений: tg φ 0, Q 0, E q0. Необходимо учесть, что при изменении cos φ 0 Р 0 остается неизменной, а изменяется Q 0.
Графики Р пр = f 1(cos φ 0) и К зп = f 2(cos φ 0) строятся на одном рисунке, центральная точка оси абсцисс должна соответствовать cos φ 0 = 1, слева от нее располагаются точки для отстающих токов, справа – для опережающих.
5.1.2. ОПРЕДЕЛЕНИЕ ПРЕДЕЛА ПЕРЕДАВАЕМОЙ МОЩНОСТИ С УЧЕТОМ ЯВНОПОЛЮСНОСТИ ГЕНЕРАТОРОВ ПРИ ОТСУТСТВИИ АРВ
Для участка системы от генератора G 1 до шин нагрузки определяются результирующие сопротивления Х dрез и Х qрез:
Х dрез = Х d + Х рез.вн; Х qрез = Х q + Х рез.вн
ЭДС генераторов определяется графоаналитическим путем в соответствии с вектороной диаграммой (рис. 5.1.в). Сначала проводится горизонтальная линия на которой в выбранном масштабе откладывается вектор U н. Затем рассчитывается величина ЭДС Е Q
Далее необходимо определить угол δ0, для чего вычисляется тангенс этого угла по формуле:
Остальные параметры для построения векторной диаграммы находятся по следующим формулам:
; 
; 
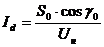Передаваемая мощность определяется выражением из двух составляющих (рассчитывается при условии sin δ = sin δ 0);
максимальные значения составляющих (определяется при Е q = Е q0)
, 
Затем исследуя выражение для передаваемой мощности на максимум, находим
Рассчитав δ М можно определить предельную мощность
Далее определяется коэффициент запаса
Затем в одной системе координат строятся графики предельной передаваемой мощности Р пр = f (δ) и ее составляющих Р m1 = f 1 (δ) и Р m2 = f 2 (δ). График Р пр = f (δ) можно получить путем графического сложения синусоидальных зависимостей составляющих. Предельная передаваемая мощность и коэффициент запаса, очевидно, должны несколько превышать значения, полученные ранее (см. п. 5.1.1), где производился расчет предельной передаваемой мощности без учета явнополюсности генераторов установленных на первой станции.
5.1.3. РАСЧЕТ ПРЕДЕЛА ПЕРЕДАВАЕМОЙ МОЩНОСТИ ПРИ НАЛИЧИИ АРВ ПРОПОРЦИОНАЛЬНОГО ТИПА
Основные условия для расчета предела передаваемой первой станцией мощности те же, что и в п. 5.1.1. Для АРВ пропорционального типа принято характеризовать генераторы неизменной ЭДС Е ’q за переходным сопротивлением и реактивностью Х ’d, которая находится по выражению:
Далее находится предел передаваемой мощности
и коэффициент запаса К зп.
5.1.4. РАСЧЕТ ПРЕДЕЛА ПЕРЕДАВАЕМОЙ МОЩНОСТИ ПРИ НАЛИЧИИ РЕГУЛЯТОРОВ ВОЗБУЖДЕНИЯ СИЛЬНОГО ДЕЙСТВИЯ
В этом случае напряжение на шинах генератора первой станции считается неизменным, что учитывается введением в выражение Х рез.вн
далее находится предел передаваемой мощности по выражению:
,
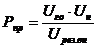а затем коэффициент запаса устойчивости К кз.
5.1.5. ОПРЕДЕЛЕНИЕ ПРЕДЕЛА ПЕРЕДАВАЕМОЙ МОЩНОСТИ С УЧЕТОМ ДЕЙСТВИТЕЛЬНЫХ ПАРАМЕТРОВ ВТОРОЙ СТАНЦИИ
В предыдущих расчетах напряжение на шинах нагрузки считалось неизменным, т.е. мощность второй станции – неограниченной. В данном подразделе необходимо учесть действительную мощность второй станции. Сопротивление нагрузки считается неизменным, ЭДС генераторов определяются из исходного режима и считаются также постоянными (АРВ отсутствует). Поскольку явнополюсность генераторов не учитывается, то ЭДС обоих источников (см. рис. 5.1.а) определяются как и в п. 5.1.1.
ЭДС первой станции принимается по пункту 5.1.1. следовательно Е q0 = Е 0. Мощность, посылаемая в нагрузку второй станцией, находится из следующих соотношений:
; 
,
где Р 0 и Q 0 мощности определяемые в п. 5.1.1. Мощность Р нг определяется в относительных единицах с учетом S б.
Мощность, выдаваемая первой станцией, рассчитывается по формуле
.
Предварительно ЭДС второй станции находится по выражению:
.
где Х э2 эквивалентное сопротивление второй станции равное
.
В данном выражении Х 6 и Х 8 реактивности трансформаторов Т 3 и Т 4 соответственно, Х 7 и Х 9 реактивности генераторов G 2 и G 3 соответственно (вторая станция). Символ ║означает параллельное соединение.
Находятся следующие составляющие:
y 11 – модуль собственной эквивалентной проводимости первой станции; собственная проводимость определяет величину и фазу составляющей тока от действия ЭДС в данной ветви при ЭДС во всех остальных ветвях равных нулю. Например, I 11 = E 1· y 11.
y 12 – модуль взаимной эквивалентной проводимости между первой и второй станциями; взаимная проводимость y 12 определяет величину и фазу тока I 12 в ветви 1 от действия ЭДС приложенной к ветви 2 при равенстве нулю ЭДС во всех остальных ветвях. Например: I 12 = Е 2 · y 12.
Углы: 
и 
характеризуют соотношение между составляющими полных собственных и взаимных сопротивлений электрической сети.
Угол 
представляет собой разность между углами δ первой и второй станций.
Модули проводимостей y 11 и y 12 и углы 
и 
определяются из приводимых соотношений, причем для проводимостей предварительно находятся значения соответствующих полных сопротивлений по значениям их составляющих.
Собственное сопротивление
; 
,
где 
, причем φ 1 = 900 т.к. сопротивление чисто индуктивное.
Z нг = r нг + j X нг = Z нгּexp(jφ нг); φ нг – определяется по исходным данным из cos φ для нагрузки.
; 
Взаимные сопротивление, проводимость и угол
; 
;
; 
.
Угол 
находится по значению 
, значения Х 12 и r 12 берутся по абсолютной величине и определяются по выражению:
где 
; следует учесть что r 1 = r 2 = 0.
Значения величин в приведенных формулах определяются применительно к схеме рис. 5.1.а.
Необходимо сделать проверку формулы для Р 1 по исходному режиму, для чего находится исходный угол δ 0:
;
;
.
Далее рассчитывается значение мощности выдаваемое первой станцией Р 10 при δ 12 = δ 0, используя выражение для Р 1, которое представляется в следующем виде:
,
где 
, 
;
оценивается ошибка (%):
.
Рассчитывается предельная передаваемая мощность по формуле для Р 1 в которой принимается 
. Угол максимума передаваемой мощности 
.
По результатам расчетов для всех пяти задач (5.1.1 – 5.1.5) составляется сводная таблица с указанием численных значений рассчитанных величин Р пр, К зп, δ м. На отдельном рисунке строятся графики зависимостей Р = f (δ). Точно наносятся только координаты Р = 0 и Р = Р пр, остальные части кривых могут быть построены приближенно, учитывая синусоидальную зависимость Р = f (δ). Для пп. 5.1.2 и 5.1.5 следует привести также вид отдельных составляющих общей передаваемой мощности. Для всех графиков нанести значения угла δ м.
5.2. РАСЧЕТ ПРЕДЕЛЬНОГО ВРЕМЕНИ ОТКЛЮЧЕНИЯ КОРОТКОГО ЗАМЫКАНИЯ. ДИНАМИЧЕСКАЯ УСТОЙЧИВОСТЬ.
5.2.1. ТРЕХФАЗНОЕ КОРОТКОЕ ЗАМЫКАНИЕ
Точка короткого замыкания «К » находится в начале линии ВЛ 2, следовательно, при трехфазном к.з. в этой точке передача активной мощности от G 1 прекращается (Р IIm = 0). Послеаварийным является режим с работой линии ВЛ 1 и отключенной ВЛ 2, что учитывается при расчете Х ’dрез введением внешнего сопротивления Х вн с учетом одной работающей линии. Расчет следует вести по условиям п.5.1.3. Если запас устойчивости при работе одной линии меньше 15 %, то следует в качестве послеаварийного принять исходный режим при работе двух линий (успешное АПВ). Сначала на основании формулы, вытекающей из метода площадей, находится предельный угол отключения к.з.
Углы находятся из следующих соотношений:
; 
Максимальные мощности режимов принимаются следующими:
Р Im = Р пр по п. 5.1.3 (предельная доаварийная мощность).
Р IIIm = Р пр – предельная послеаварийная мощность, рассчитанная согласно условиям данного пункта.
Значения углов δ кр и δ I0 в формулу для определения значения cosδ отк.пр подставляются в радианах.
После определения δ отк.пр необходимо провести графическую проверку, построив графики передаваемой мощности для всех трех режимов: доаварийного, послеаварийного и определить площади ускорения и торможения. Проверку можно выполнить путем графической оценки соответствующих площадей. Графики строятся на миллиметровой бумаге. Построение угловых характеристик выполняется учитывая синусоидальный характер зависимостей Р = f (δ).
После вычисления площадей (например, в мм2) оценивается погрешность в процентах:
При Р IIm = 0 движение ротора генератора является равноускоренным и предельное время отключения к.з. находится по формуле
.
В этой формуле Т1 должно быть выражено в секундах, углы в радианах, Р0 – в относительных единицах. Если номинальная мощность генератора G1 и базисная мощность не равны друг другу, то необходимо сделать пересчет постоянной времени:
.
5.2.2. ДВУХФАЗНОЕ КОРОТКОЕ ЗАМЫКАНИЕ НА ЗЕМЛЮ.
РАСЧЕТ БЕЗ УЧЕТА РЕАКЦИИ ЯКОРЯ И АРВ
Необходимо составить схемы замещения для токов прямой, обратной и нулевой последовательностей (рис. 5.2, а, б, в) и найти результирующие сопротивления Х 2рез и Х 0рез. ЭДС Е ’q может быть взята по результатам расчета (см. п. 5.1.3).
а
б
в
г
Рис. 5.2.
Схему прямой последовательности в данной задаче не следует преобразовывать. Необходимо в точке «К » для определения токов прямой последовательности подключить шунт с результирующим сопротивлением, которое рассчитывается по выражению:
.
Предварительно находятся составляющие сопротивления шунта, включаемого в т. «К ».
Сопротивление обратной последовательности находится по схеме, представленной на рис. 5.2.б:
где Х 2 – сопротивление обратной последовательности генератора G 1; Х л – результирующее сопротивление двух параллельно работающих воздушных линий для токов прямой (и обратной) последовательности; Х Т1 и Х Т2 – сопротивления прямой (и обратной) последовательности для трансформаторов Т 1 и Т 2 соответственно.
Сопротивление нулевой последовательности
,
где Х л0 – результирующее сопротивление двух параллельно работающих воздушных линий токами нулевой последовательности.
Комплексная схема замещения, свернутая для определения токов прямой последовательности, приведена на рис. 5.2.г. Расчет мощности, передаваемой генераторами в систему при двухфазном замыкании на землю, выполняется аналогично расчету мощности в п. 5.1.5. Однако в данной схеме сопротивление шунта Х к чисто реактивное, поэтому φ 11 = 900, α 11 = 0 и первое слагаемое мощности равно нулю. Взаимное сопротивление определяется по следующему выражению:
,
где 
; (Х’d – переходное сопротивление генератора G1, определенное для базисных условий); 
; φ 12 = 900, α 12 = 0.
Далее находится передаваемая станцией мощность в аварийном режиме Р IIm.
.
В данной формуле Е ’q – принимается по п. 5.1.3; δ 12 = δ I0.
Исходный Р Im и послеаварийный P IIIm 
режимы принимаются по п. 5.2.1. Зная δ I0, δ кр, Р 0, Р IIm, P IIIm можно рассчитать предельный угол отключения двухфазного к.з. на землю δ (1,1) отк.пр. Затем, как и в п. 5.2.1, следует построить графики Р (δ) и сделать графически проверку по методу площадей (рис. 5.2.д).
Для нахождения предельного времени отключения к.з. необходимо рассчитать зависимость угла δ от времени в аварийном режиме методом последовательных интервалов, для чего задаются шагом интегрирования Δ t = (0,02 – 0,05) с и рассчитывают постоянный коэффициент
; f = 50 Гц
После этого заготавливают таблицу с графами для значений t, δ нач, sin δ нач, Р II, Δ Р, К · Δ Р, Δ δ, δ конеч. Процесс ускорения ротора начинается от времени t = 0 и угла δ = δ I0.
Для первого интервала
; 
;
; 
.
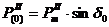Для второго интервала
; 
;
; 
.
Остальные интервалы рассчитываются аналогично второму. Расчет ведется до достижения угла, большего δ отк.пр. По графику δ (t) находится время t отк.пр соответствующее предельному углу отключения δ отк.пр.
5.2.3. ДВУХФАЗНОЕ КОРОТКОЕ ЗАМЫКАНИЕ НА ЗЕМЛЮ.
РАСЧЕТ С УЧЕТОМ РЕАКЦИИ ЯКОРЯ И ДЕЙСТВИЯ АРВ
За счет АРВ ординаты кривой передаваемой в аварийном режиме мощности Р II (δ) постепенно увеличиваются во времени, по сравнению с кривой, когда генераторы работают без АРВ. Увеличивается и предельный угол отключения к.з., однако непосредственно по формулам его величина не может быть определена. В связи с этим необходимо рассчитать три варианта кривых δ = f (t), задаваясь тремя значениями t отк. Если угол δ проходит через максимум и далее уменьшается, то динамическая устойчивость обеспечивается, т.е. принятое условие выполняется, t отк < t отк.пр. Если же угол δ неограниченно возрастает, то это говорит о нарушении динамической устойчивости, т.е. t отк > t отк.пр. В качестве первоначального значения t отк можно принять значение t отк.пр из предыдущего расчета (п. 5.2.2). Величину интервала времени целесообразно взять равной Δ t = 0,01 с. Передаваемая в систему электрическая мощность в аварийном режиме определяется в соответствии со схемой (рис. 5.2.г), в которой ЭДС Е ’q заменяется на ЭДС Е q, Х 1э = Х d + Х r1. Для исходного режима (t = 0) значения Е q0 и δ могут быть приняты по п. 5.1.1, а для Е ’q0 – по п. 5.1.3.
В первый момент нарушения режима
где для чисто реактивных схем α 11 = α 12 = 0.
Далее рассчитывается кривая ЭДС источника возбуждения
,
где К пр = I *fпр - потолок возбуждения.
Для каждого интервала времени определить среднее значение Е qe как полу-сумму начального и конечного значений.
Изменение переходной ЭДС за первый интервал составляет
.
Переходная ЭДС в конце первого интервала равна
Электрическая мощность в начале первого интервала
.
Мощность ускоряющая ротор
.
Приращение угла составляет
.
Угол в конце первого интервала времени
Для второго интервала времени параметры соответственно равны:
;
;
;
; 
;
; 
.
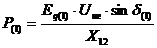Последующие интервалы до момента времени t = t отк рассчитываются аналогично второму. После отключения к.з. в формулу для Е q(1) следует вместо y 11 и y 12 подставлять величину
,
где Х dрез – результирующее сопротивление связи источника Е q с шинами U нг в послеаварийном режиме.
Расчет данного режима к.з. производится на ЭВМ с использованием программы «DINSG». Согласно схемы замещения (см. рис. 5.2.г) рассчитываются сопротивления и проводимости:
где Х d – реактивное сопротивление первого генератора, Х r1 – сопротивление прямой последовательности Т 1.
,
где Х 2э и Х к – реактивные сопротивления схемы замещения принимаемые по п. 5.2.2.
; 
; 
Для ввода в ЭВМ необходимо составить перечень вводимых данных, которые принимаются из предварительного расчета или согласно условиям работы принимаемой программы.
ВВОДИМЫЕ ОПЕРАТОРЫ
Х1 = 0 – начальное время расчета;
Х2 = tрасч - конечное время расчета переходного процесса в секундах
(Х2 = (2-3) tотк.пр), согласно п. 5.2.2;
N1 = tрасч/Н1, где Н1 – шаг по времени;
N2 = 55 – число точек по оси углов;
N3 = 7 – число выводимых кривых;
M1 = 1 – число распечаток;
L1 = 1 – вывод графика, 2 – таблицы, 3 – графика и таблицы;
РТ = Р0 – мощность турбины;
EQO = Еq0 – принимается по п. 5.1.1;
EQPO = Е’q(0) – принимается по п. 5.1.3;
U = 1 – номинальное напряжение в относительных единицах;
XD = Х*d(б) – реактивное сопротивление G1;
XD1 = Х’*d(б) – переходное реактивное сопротивление G1;
Y11А = yА11 (аварийный режим);
Y12А = yА12 (аварийный режим);
XDC2 = Х*d(б) + Х*рез.вн(б), Х*рез.вн(б) – при работе в послеаварийном
режиме;
Н1 = 0,01 (шаг по времени в секундах);
К2 = 2 (Δtвывода/Δtрасч);
К3 = 6 (Δtотк.пр/Δtрасч);
KPR = Кпр = I*fпр – потолок (предельный ток) возбуждения;
DO = δ 0 – принимается по п. 5.2.1 в радианах;
N4 = 5 – число вариантов для δ (по отключению);
ТК = Х2;
ТОТК = tотк.пр – по п. 5.2.2 (начальное значение расчета);
TI = ТI – постоянная инерции вращающихся масс турбины и
генератора (электромеханическая);
TD = Тd – постоянная времени демпферной цепи;
ТЕ = Те – постоянная времени цепи возбуждения.
На распечатанных графиках приняты следующие обозначения переменных: цифрой 1 - Еq; 2 - Е’q; 3, 4, 5, 6, 7 – углы δ.
Используя полученные графики требуется определить предельное время отключения генератора в аварийном режиме. Если за полученное время переходного процесса уверенно сделать это не удается, повторить расчет увеличив выбранное время.
При защите курсовой работы необходимо:
- иметь четкие представления о работе предлагаемых для расчетов схем электроснабжения и параметров их элементов;
- знать методику и порядок составления схем замещения, расчет параметров элементов схем;
- иметь четкие понятия об аварийных режимах в системах электроснабжения, видах коротких замыканий и составляющих токов к.з.;
- знать назначение проводимых расчетов и определяемые характеристики;
- уметь выполнять аналитический и графический расчет определяемых характеристик (использование метода типовых кривых, построение угловых характеристик передаваемой мощности, метод последовательных интервалов и т.д.);
- иметь четкое представление о режимах работы электрических систем, видах их устойчивости, назначении входящих в них элементов;
- знать назначение и виды АРВ, эффективность их действия и влияние на вид угловых характеристик передаваемой мощности;
- знать методы определения критических параметров для аварийных режимов при расчете электромеханических переходных процессов и уметь объяснить их сущность;
- знать принцип построения угловых характеристик передаваемой мощности и закономерности их изменения в различных режимах;
- знать особенности работы явнополюсных и неявнополюсных синхронных генераторов.
Приложение
Значения отношений сопротивлений прямой последовательности 
в зависимости от номинальной мощности трансформатора (автотрансформатора) – а, б;
Значения отношений сопротивлений нулевой последовательности 
трансформаторов при соединении обмоток Y0 / Y0 и трехстержневом магнитопроводе – в.
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1. Ульянов С.А. Электромагнитные переходные процессы в электрических системах. – М.: Энергия, 1970. – 520 с.
2. Электромагнитные переходные процессы в электрических системах: Текст лекций / В.А.Стеблев; Самар.гос.техн.ун-т;Самара.: 1993. – 44 с.
3. Винославский В.Н., Пивняк Г.Г., Несен Л.И. и др. Переходные процессы в системах электроснабжения: Учебник / Под ред. В.Н.Винославского. – К.: Выща шк. Головное изд – во, 1989. – 422 с.
4. Электрическая часть станций и подстанций: Справочные материалы для курсового и дипломного проектирования. / Под ред. Б.Н.Неклепаева. – М.: Энергия, 1978. – 420 с.
5. Расчет токов короткого замыкания в системах электроснабжения: Методические указания к курсовому и дипломному проектированию для студентов специальности 0303 / А.Д.Герлейн; КПтИ; Куйбышев.: 1981. – 38 с.
6. Чунихин А.А. Электрические аппараты. – М.; Энергоатомиздат, 1988. – 720 с.
7. Переходные процессы в системах электроснабжения: Задания на курсовые работы / Сост. Н.Н.Родионов, А.Д.Герлейн; Самар.гос.техн.ун-т; Самара, 1999. – 20 с.
8. Веников В.А. Переходные электромеханические процессы в электрических системах. – М.: Высш. Школа, 1985. – 536 с.
9. Крючков И.П. и др. Электрическая часть станций и подстанций: Справ: мат-лы для курсового и дипломного проектирования. – М.: Энергия, 1978. – 456 с.
10. Переходные процессы в электрических системах в примерах и иллюстрациях / Под ред. В.А.Веникова. – М.: Госэнергоиздат, 1967. – 456 с.
СОДЕРЖАНИЕ
1. Общие сведения 3
2. Электромагнитные переходные процессы 3
2.1. Основные допущения при расчете токов к.з. 5
2.2. Составление схем замещения 6
2.3. Применение систем относительных единиц для
расчета токов к.з. 9
2.4. Приведение параметров элементов систем к одной ступени
напряжения 10
2.5. Расчет параметров элементов системы электроснабжения 11
2.5.1. Эквивалентный источник питания – система 11
2.5.2. Трансформаторы и автотрансформаторы 12
2.5.3. Реакторы 15
2.5.4. Линии электропередач 16
2.5.5. Обо