Тема: Кинематический анализ механизмов

Кинематическая структура манипулятора определяет число звеньев и тип кинематических пар их соединения.

Рабочая зона робота – пространство, в котором может находиться его рабочий орган.

Объем рабочей зоны V_рз (м³) – объем, заключенный внутри границ рабочей зоны.

Тип системы координат определяется сочетанием кинематических пар.

Тип системы программного управления (СПУ)определяется способом позиционирования (цикловой, позиционный, контурный) и типом применяемых аппаратных средств.

Роботизированным участкам, линиям и цехам присущи следующие качества: наличие транспортно-складской системы и единой системы управления. Эти системы материально и информационно связывают отдельные технологические ячейки, автоматизированные склады (материалов, заготовок, инструмента, отходов производства, готовой продукции) и другие части комплекса в одну согласованно действующую систему. На рис.1 показан пример простой линейной компоновки однопоточной роботизированной технологической линии с непосредственной связью между составляющими линию ячейками. В ней отсутствует межоперационная транспортная система, а предметы производства передаются от одной ячейки к другой непосредственно входящими в них вспомогательными ПР. Такие линии с непосредственной жесткой связью между ячейками просты, однако требуют строго определенного взаимного расположения основного технологического оборудования.

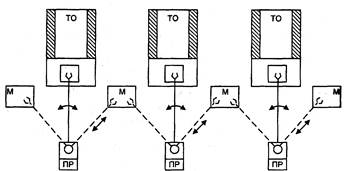
Рис.1. Схема однопоточной роботизированной технологической линии холодной штамповки с линейной компоновкой: ТО — основное технологическое оборудование; ПР — промышленный робот; М — магазин поштучной выдачи заготовок

Данная компоновка характерна для технологических процессов с малым циклом обработки предметов производства на технологическом оборудовании (единицы, десятки секунд). Для технологических процессов с большей длительностью обработки на технологическом оборудовании часто применяют другой тип построения комплексов с обслуживанием одним ПР нескольких единиц технологического оборудования. На рис.2 показан вариант такого комплекса с круговой компоновкой, в котором один ПР обслуживает 3 металлорежущих станка, расположенных вокруг него.

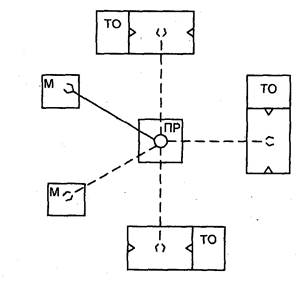
Рис.2. Схема роботизированного технологического участка механической обработки с круговой компоновкой

Манипулятор – устройство для выполнения двигательных функций, аналогичных функциям руки человека при перемещении объектов в пространстве, оснащенное рабочим органом. Манмпулятор имеет кинематическую цепь, образованную последовательным или последовательно-параллельным соединением тел, называемых кинематическими звеньями, и предназначенную для преобразования движения этих звеньев в требуемое (заданное) движение рабочего органа или схвата. При этом кинематические звенья соединяются друг с другом подвижно с помощью кинематических пар.

Кинематическая цепь, образующая манипулятор, имеет два оконечных звена: одно из них будет являться основанием – стойкой (ему присваивается нулевой номер), а другое оконечное звено оснащается схватом. Этому оконечному звену присваивается последний n-й номер, равный при последовательном соединении звеньев числу подвижных звеньев манипулятора.

Кинематическое звено – совокупность жестко соединенных друг с другом тел, входящих в состав механизма, в данном случае в состав манипулятора.

Кинематическая пара – подвижное соединение двух кинематических звеньев, допускающее их вполне определенное движение относительно друг друга. Элементы кинематической пары – поверхности, линии или точки, по которым соприкасаются звенья, образующие данную кинематическую пару.

Кинематическая цепь – это совокупность кинематических звеньев, подвижно соединенных друг с другом с помощью кинематических пар.

Если в кинематической цепи есть кинематические звенья, входящие в одну кинематическую пару, то такая цепь называется разомкнутой, а если же каждое звено входит, как минимум, в две кинематических пары, то это замкнутая кинематическая цепь.

 

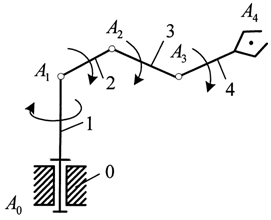
Рис. 3. Манипулятор на основе разомкнутой цепи

Манипулятор может быть образован как на основе разомкнутой кинематической цепи с последовательным соединением звеньев (антропоморфные человекоподобные роботы) и на основе замкнутой кинематической цепи с последовательно-парал­лель­ным соединением звеньев (роботы с параллельной кинематикой, в частности, гексаподы на основе платформы Стюарта).

В некоторых областях техники перспективным является применение роботов-манипуляторов на основе механизмов параллельной кинематики, используемых при механической обработке изделий сложной формы (например, штампов, пресс-форм, лопаток турбин и т. д.), когда требуется перемещение инструмента по пяти-шести координатам. В отличие от традиционных манипуляторов, структуры с параллельной кинематикой содержат замкнутые кинематические цепи и воспринимают нагрузку как пространственные фермы, т.е. звенья этих механизмов работают на растяжение и сжатие, что обеспечивает жесткость всей конструкции и, как следствие, повышение точности позиционирования схвата.

Трехмерное моделирование кинематически сложных механизмов целесообразно выполнять с помощью системы автоматизированного проектирования (САПР) CATIA, в которой используются алгоритмы моделирования движения кинематически сложных механизмов, таких как устройства параллельной кинематики. Для решения систем уравнений, описывающих положение устройства параллельной структуры, наиболее подходящим является программный пакет Maple – система компьютерной алгебры, позволяющая решать сложные системы уравнений как в численном, так и в символьном виде.

Постановка задачи. Рассмотрим устройство параллельной кинематики – дельта-механизм (рис.4), включающий в себя основание, образованное точками 3, 6, 9, верхнюю платформу, на движение которой накладывают ограничения три кинематические цепи: 1–2–3, 4–5–6, 7–8–9. В точках 1, 2, 4, 5, 7, 8 установлены поворотные шарниры с одной вращательной степенью свободы, в точках 3, 6, 9 – сферические шарниры с тремя вращательными степенями свободы.

Основание и поворотная платформа представляют собой равносторонние треугольники. Введем следующие обозначения элементов дельтамеханизма (рис.4):

- x_ij, y_ij, zi_j – координаты i-й точки в j-й системе координат;

- li – длина i-го звена, во всех кинематических цепях l₁ = 37 мм, l₂ = 58 мм;

- φ_ij – угол i-го шарнира в j-й кинематической цепи;

- δi – угол между первой системой координат i-й кинематической цепи и базовой системой координат, δ1 = 330°, δ2 = 210°, δ3 = 90°;

- E – расстояние между сферическими шарнирами 3, 6, 9 дельта-механизма, E = 60 мм;

- F – расстояние от начала базовой системы координат до поворотных шарниров 1, 4, 7, F = 60 мм;

- R – расстояние от полюса схвата P до сферических шарниров 3, 6, 9, R = 34,641 мм;

- Х₀Y₀Z₀ – базовая система координат;

- Х₁Y₁Z₁ – первая система координат.

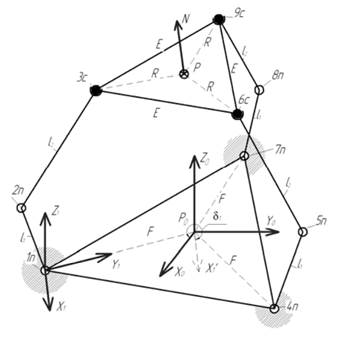
Рис. 4. Общий вид дельта-механизма

Решение прямой задачи кинематики. Прямая задача кинематики манипуляторов применительно к дельта-механизму сводится к нахождению координат поворотной платформы при заданных длинах звеньев l1, l2 и углов поворотов шарниров φ₁₁, φ₂₁, φ₁₂, _φ22, φ₁₃, φ₂₃ (рис. 5).

Для решения этой задачи сначала находят координаты сферического шарнира (точки 3) в первой системе координат X₁Y₁Z₁, а затем с помощью переноса на расстояние F и поворота на угол δ переходят к базовой системе координат X₀Y₀Z₀. Аналогично определяют координаты остальных сферических шарниров – точек 6, 9, которые вместе с точкой 3 задают плоскость поворотной платформы (рис. 3). По уравнению этой плоскости можно найти углы ее наклона в базовой системе координат X₀Y₀Z₀, а также высоту полюса схвата.

 

 

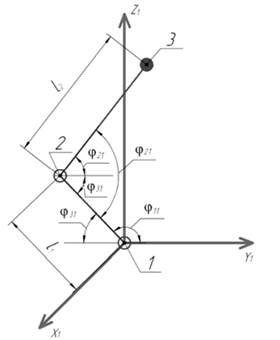
Рис.5. Определение положения точек 2 и 3 в первой системе координат

От характера кинематических пар и от их взаимного расположения в манипуляторе зависят законы преобразования движения. Кинематические пары допускают вполне определенные движения образующих их звеньев относительно друг друга. Эта определенность достигается теми ограничениями, которые создают пары геометрией своих элементов.

Пары классифицируют по классам, номер которого равен числу ограничений (числу условий связи), накладываемых данной парой:

- одно ограничение (одно условие связи) – пара I класса;

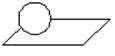
- два ограничения (два условия связи) – пара II класса;

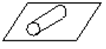
- три ограничения (три условия связи) – пара III класса;

- четыре ограничения (четыре условия связи) – пара IV класса;

- пять ограничений (пять условий связи) – пара V класса (пары пятого класса могут быть поступательными и вращательными).

Примеры условных обозначений кинематических пар пятого класса как наиболее часто используемых в манипуляторах ПР.

Вращательная пара, соединяющая подвижные звенья

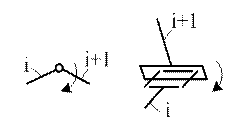
Вращательная пара, соединяющая неподвижное звено (стойку) с подвижным

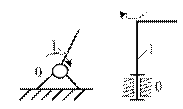
Поступательная пара, соединяющая подвижные звенья

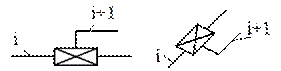
Поступательная пара, соединяющая неподвижное звено (стойку) с подвижным

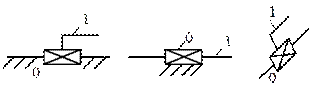
Важной характеристикой манипулятора является число степеней его подвижности (W), число степеней свободы. Для определения W произвольной кинематической цепи следует использовать формулу Сомова – Малышева.

,

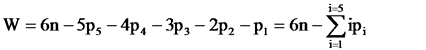где p_i – число кинематических пар i-го класса.

Для манипуляторов с кинематическими парами 5- го класса

.

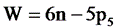Так как в манипуляторе с последовательной кинематикой каждому подвижному звену соответствует одна кинематическая пара пятого класса, то 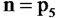. Следовательно, 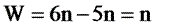или 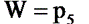, то есть число степеней подвижности в таких манипуляторах равно числу подвижных звеньев и числу кинематических пар.

В манипуляторах в основном используются одноподвижные вращательные или поступательные пары 5-го класса. Для определенности движения одного звена относительно другого в случае, если они подвижно соединены парой 5-го класса требуется задание одного перемещения. Это легко реализуется современными двигателями.

Система координат (СК), или система координатных перемещений, ПР определяет кинематику основных движений и форму рабочей зоны (зоны обслуживания манипулятора). Системы координат бывают двух видов: прямоугольные и криволинейные.

1. Плоская прямоугольная СК.

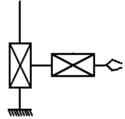
Объект манипулирования перемещается в одной плоскости за счет 2-х взаимно перпендикулярных направлений.

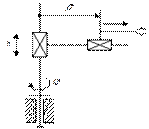
1. Пространственная прямоугольная СК.

Отличается относительной простотой и целесообразна при прямолинейном перемещении УЗ.

2. Плоская полярная СК. Перемещение объекта происходит в одной плоскости в направлении радиус-вектора r и угла поворота j.

3. Цилиндрическая СК.

 

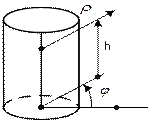
Характеризуется перемещением объекта в основной координатной плоскости в направлениях r и j, а также по нормали к ней z.

4. Сферическая (полярная) СК.

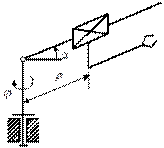
Перемещением объекта манипулирования в пространстве осуществляется за счет линейного движения руки ПР на величину r и ее угловых перемещений j и q в двух взаимно перпендикулярных плоскостях.

Плоские полярные, цилиндрические и сферические перемещения объекта манипулирования являются наиболее распространенными в криволинейной СК. Разновидностью последней являются ангулярная (угловая) плоская и ангулярная пространственная (цилиндрическая или сферическая) СК.

5. Ангулярная плоская СК.

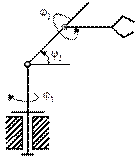
В ангулярной плоской СК объект манипулирования перемещается в координатной плоскости благодаря относительным поворотам звеньев руки М, имеющих постоянную длину.

6. Ангулярная цилиндрическая СК. Ангулярная цилиндрическая СК характеризуется дополнительным смещением руки М относительно основной координатной плоскости в направлении перпендикулярной к ней координаты z.

7. Ангулярная сферическая СК. В ангулярной сферической СК перемещение объекта в пространстве происходит только за счет относительных угловых поворотов звеньев руки М. При этом хотя бы одно звено должно иметь возможность поворота на углы j и q в двух взаимно перпендикулярных плоскостях.

Мехатронные и робототехнические системы в отдельных случаях могут иметь количество степеней подвижности более шести.

Чтобы не вносить помехи в положение схвата или свести их к минимуму, ориентирующие степени подвижности делают так, чтобы они как можно меньше перемещали схват.Манипуляционные системы, обеспечивающие ориентирующие движения схвата.

1. Обеспечение полной пространственной ориентации схвата:

2. Ротация с дополнительным пространственным движением схвата:

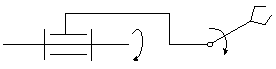
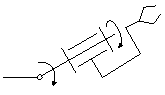
3. Ротация схвата:

4. Без ориентирующих степеней подвижности (в этом случае оборудование расставляется так, чтобы рука робота оказывалась в требуемом относительно него положении).

Твердые тела, входящие в состав исполнительного меха­низма и являющиеся функциональными элементами его кине­матической цепи называются звеньями. Звено исполнительного механизма конструктивно может состоять из нескольких дета­лей, не имеющих между собой относительного движения.

Соединение двух соприкасающихся звеньев, допускающих их относительное движение, называется кинемати­ческой парой. Совокупность поверхностей, линий и точек звена, входящих в соприкосновение (контакт) с другим звеном па­ры, называется элементом пары. Для того, чтобы элементы па­ры находились в постоянном соприкосновении, пара должна быть замкнута геометрическим (за счет конструктивной формы звеньев) или силовым (силой тяжести, пружиной, силой давле­ния жидкости или газа и т.п.) способом.

Контактирующие поверхности, линии и точки звеньев, являющиеся элементами кинематической пары, могут образовывать простые и сложные кинематические пары. В простой кинематической паре (рис. 6 а) контактируют только два эле­мента 1 и 2, которые определяют соответствующее число ком­понент реакций связей. В сложной паре (рис. 6 б) необходимые геометрические связи дублируются дополнительными связями 11 и 21. Дополнительные элементы кинематических пар вводят для уменьшения давления и износа контактирующих поверхно­стей за счет перераспределения реактивных сил и увеличения размеров элементов кинематических пар.

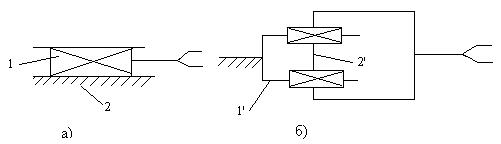
Рис. 6. Кинематические пары: а) простые, б) сложные

Если помимо необходимых элементов кинематической пары, обусловленных требуемыми геометрическими связями, при конструировании используют дополнительные элементы, то в такой сложной кинематической паре могут появиться избыточные локальные связи. При наличии избыточных локальных связей относительное движение звеньев либо становится невоз­можным (заклинивание, защемление элементов), либо осуществляется за счет деформации звеньев, увеличенных зазоров между реальными поверхностями элементов или их износа.

Чтобы кинематическая пара была работоспособной и надежной в эксплуатации, предъявляют определенные требова­ния к размерам, форме и относительному положению ее эле­ментов. Обычно указывают пределы отклонений от заданных или требуемых геометрических форм и расположения поверхностей, осей или точек.

Схема кинематической пары, отражающая только необходимое число геометрических связей, соответствующее вид} пары называется основной. Схема кинематической пары, отражающая как необходимые, так и избыточные локальные (дополнительные) связи, называется действительной. Избыточ­ные локальные связи вносят статическую неопределимость. Число избыточных локальных связей в реальной кон­струкции пары называется степенью статической неопредели­мости кинематической пары. Применение сложных кинемати­ческих пар с избыточными локальными связями возможно при достаточной жесткости звеньев, когда их деформация при воздействии нагрузок не приводит к заклиниванию элементов кинематических пар или их повышенному изнашиванию.

Исполнительные механизмы, удовлетворяющие требова­ниям приспособляемости к деформациям звеньев, надежности, долговечности и технологичности конструкции, обладают оптимальной структурой. Оптимальная система расположения элементов кинема­тической пары - понятие относительное: конструкция опти­мальная для одних условий, может быть неприемлемой для других. Часто это связано с технологичностью, как совокупностью свойств конструкции, проявляемых при оптимальных затратах труда, средств, материалов и времени при принятых условиях изготовления, эксплуатации и ремонта промышленного робота. Конструкция, достаточно технологичная в единичном произ­водстве, часто оказывается малотехнологичной в массовом производстве и совершенно нетехнологичной в автоматизирован­ном производстве.

Кинематические пары классифицируют по числу связей (ограничений), налагаемых парой на относительное движение звеньев на кинематиче­ские пары пятого, четвертого, третьего, второго и первого классов (рис. 7).

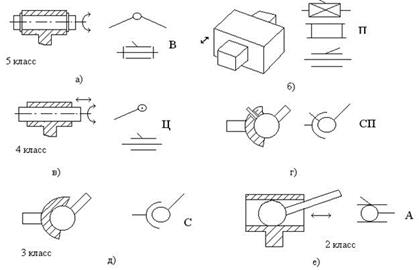
Рис. 7. Примеры кинематических пар.

По характеру соприкосновения звеньев кинематические пары делят на низшие, если элементы звеньев соприкасаются только по поверхности, и высшие, если элементы звеньев со­прикасаются только по линиям или в точках. При этом линей­ный или точечный контакт понимается как первоначальный при соприкосновении звеньев без усилия, а под нагрузкой звенья, образующие высшую пару, будут соприкасаться по не­которой фактической поверхности, называемой пятном контакта.

Преимущество низших кинематических пар по сравнению с высшими - возможность передачи больших сил, по­скольку контактная поверхность соприкасающихся звеньев низшей пары может быть весьма значительна. Применение высших пар позволяет уменьшить трение (пример - шарико­подшипник) и получать нужные, самые разнообразные законы движения выходного звена путем придания определенной фор­мы звеньям, образующих высшую пару.

Кинематические пары во многом определяют работоспособность и надежность исполнительного устройства про­мышленного робота, поскольку через них передаются усилия от одного звена к другому; в кинематических парах, вследствие относительного движения, возникает трение, элементы пары находятся в напряженном состоянии и в процессе изнашива­ния.

Конструкция сложных кинематических пар наряду с повышением жесткости и точности должна обеспечивать непри­нужденную сборку узлов и позволять исполнительному меха­низму сохранять заданное число степеней подвижности при возможных деформациях стойки, валов, осей и других деталей под действием внешних нагрузок.

В исполнительных механизмах промышленных роботов используют кинематические пары только 5, 4 и 3 классов, но в основном кинематические пары 5- го класса. Пары 4 и 3 классов эквивалентно заменяют комбинацией двух или трех пар 5-го класса (рис. 8.), т.е. кинематическим соединением – кинематической цепью, конструктивно заменяющей в исполнительном механизме кинематическую пару.

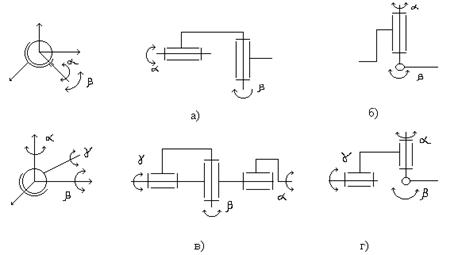
Рис. 8. Варианты замены кинематических пар высшего класса низшими.

Звено, принимаемое за неподвижное, называется основанием (стойкой). Звено, которому сообщается движение, пре­образуемое исполнительным механизмом в требуемые движения упругих звеньев, называется входным. Звено, совершающее дви­жение, для выполнения которого предназначен исполнительный механизм, называется выходным (конечным, последним).

Максимальное число входных звеньев равно числу степеней подвижности исполнительного механизма.

Звенья манипулятора соединяются друг с другом с помощью кинематических пар пятого порядка (по классификации теории механизмов и машин), вращательных и поступательных. Каждое звено имеет свое наименование. Так, с неподвижным основанием связана колонна, с колонной связана каретка, с кареткой – рука, с рукой – кисть, с кистью – захват (рис.9).

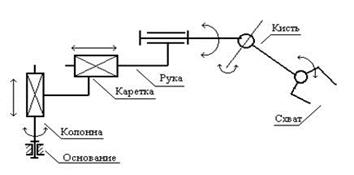
Рис. 9. Кинематика манипулятора промышленного робота.

Эти звенья образуют друг с другом кинематические пары 5-го класса, имеющие по одной степени подвижности. Каждая кинематическая пара получает движение от управляемого привода. Система звеньев, связанных между собой кинематическими парами называется кинематической цепью. В зависимос­ти от вида движения звеньев кинематические цепи подразделяют на плоские (рис10 а, в) - звенья движутся в одной или нескольких параллельных плоскостях, и пространственные (рис.10, б, г) - звенья движутся в пространстве.

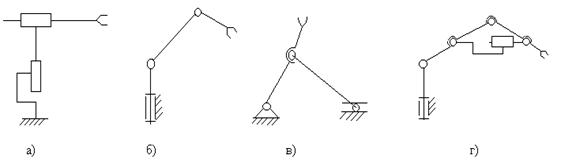
Рис. 10. Примеры кинематических цепей.

Кинематические цепи могут быть замкнутыми (рис.10,в) и незамкнутыми (рис.10, а, б, г). Кинематические цепи исполнительных механизмов ПР являются в основном нзамкнутыми. Существуют незамкнутые кинематические цепи с местными замкнутыми контурами (рис. 10, г).

Исполнительный механизм промышленного робота в процессе функционирования может иметь различную структуру. Во время движения в пространстве его можно рассматривать как незамкнутую кинематическую цепь. При выполнении тех­нологической операции на движение исполнительного меха­низма накладываются дополнительные связи и он превращается в замкнутый механизм.

Для полного осуществления пространственного движения необходимо иметь в манипуляторе шесть степеней подвижности, из них три нужны для приведения конца манипулятора в требуемую точку пространства (переносные движения), еще три – для получения необходимой угловой ориентации захватного устройства (ориентирующие степени подвижности).

Под степенями подвижности манипулятора (степенями свободы) понимают обобщенные координаты, определяющие в пространстве положения его звеньев. Число степеней подвижности манипулятора n определяется по формуле

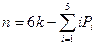
где к – число подвижных звеньев;

Рi – число кинематических пар i-го класса.

Например, в рассматриваемом случае манипулятор, изображенный на рис. 4.8. содержит 5 подвижных звеньев (исключая неподвижное основание и внутреннее подвижное звено в захвате), образующих 5 кинематических пар 5-го класса. Поэтому

n = 6*5 – 5*5 = 5.

Различают следующие степеней подвижности: координатные (глобальные) - обеспечивающие выведение манипулятора в зону манипулирования; переносные (рабочие) - определяющие выведение захвата в заданные места рабочей зоны; ориентирующие (локальные) – обеспечивающие требуемые ориентации захвата в заданном месте рабочей зоны.

Если рабочая зона является объемной, то манипулятор должен иметь не менее трех переносных степеней подвижности. В случае плоской зоны манипулирования достаточно иметь лишь две переносные степени свободы. Увеличение числа степеней подвижности усложняет манипулятор, но одновременно увеличивает его маневренность, т.е. способность обходить препятствия в рабочей зоне.

Компоновка манипулятора зависит от выбранной системы координат его функционирования. С этой точки зрения различают манипуляторы, работающие в декартовой, цилиндрической, сферической и ангулярной (угловой) системах координат. Конструкция ПР зависит и от количества рук манипуляционной системы, управляемой одним и тем же устройством управления, а также от типа устройств передвижения.