ЗАДАНИЕ ДИСТАНЦИОННОГО ОБУЧЕНИЯ
Изучить тему занятия №11 «Изгиб. Расчеты на прочность при изгибе». В рабочей тетраде письменно ответить на вопросы. После вопроса напечатать слово ОТВЕТ и напечатать (написать) ответ:
Вопросы и здания
1. Что такое изгиб?
2. Чем чистый изгиб отличается от поперечного?
3. Что такое изгибающий моменти чему он равен в сечении балки?
4. Что такое поперечная сила и чему она равна в сечении балки?
5. Каково правило определения знака для изгибающих моментов?
6. Каково правилоопределения знака для поперечных сил?
7. Как определяются внутренние силовые факторы, возникающие в поперечном сечении балки, испытывающей деформацию изгиба?
8. Как осуществляется построение эпюр изгибающих моментов и поперечных сил?
9. Какой вид имеет и как читаетсярасчетная формула на прочность при изгибе?
10. Рассчитать момент сопротивления сечения изгибу для балки прямоугольного сечения с размерами b = 50 мм и h = 100 мм. В каком положении балки (рис. 10) момент сопротивления сечения изгибу будет больше?
11. Рассчитать момент сопротивления сечения изгибу для балки круглого сечения диаметром d = 60 мм.
12. Рассчитать момент сопротивления сечения изгибу для балки кольцевого сечения с внутренним диаметром d = 40 мм и внешним диаметром D = 60 мм. 13. Для какой балки, круглого или кольцевого сечения, момент сопротивления сечения изгибу будет больше?
14. Какие профили целесообразно применять для балок, материал которых неодинаковоработает на растяжение и сжатие и почему?
Занятие №11 «Изгиб. Расчеты на прочность при изгибе»
Изгиб – это такой вид деформации, при котором в поперечных сечениях бруса возникают изгибающие моменты.
В большинстве случаев в поперечных сечениях бруса наряду с изгибающими моментами возникают поперечные силы. В этом случае изгиб называют поперечным.
Чистым изгибом называется такой вид деформации, при котором в любом поперечном сечении бруса возникает только изгибающий момент.
На изгиб работают балки, оси, валы и другие детали конструкций.
Для определения внутренних силовых факторов применим метод сечений, причем изображать балку будем только одной линией – осью, к которой приложены активные и реактивные силы. Рассмотрим два случая:
1. К балке приложены две равные и противоположные по знаку пары сил (рис. 1).
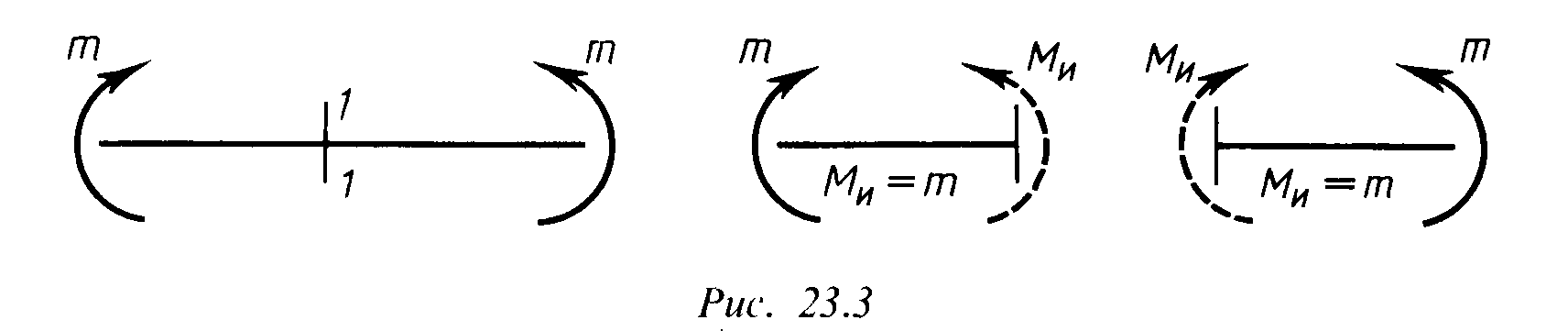
Рис. 1.
Рассматривая равновесие части балки, расположенной слева или справа от сечения 1 – 1, видим, что во всех поперечных сечениях возникает только изгибающий момент М и, равный внешнему моменту. Таким образом, рассматриваемый случай есть случай чистого изгиба.
Изгибающий момент – это результирующий момент относительно нейтральной оси внутренних нормальных сил, действующих в поперечном сечении балки.
2. К балке приложены активные и реактивные силы, перпендикулярные оси (рис. 2).
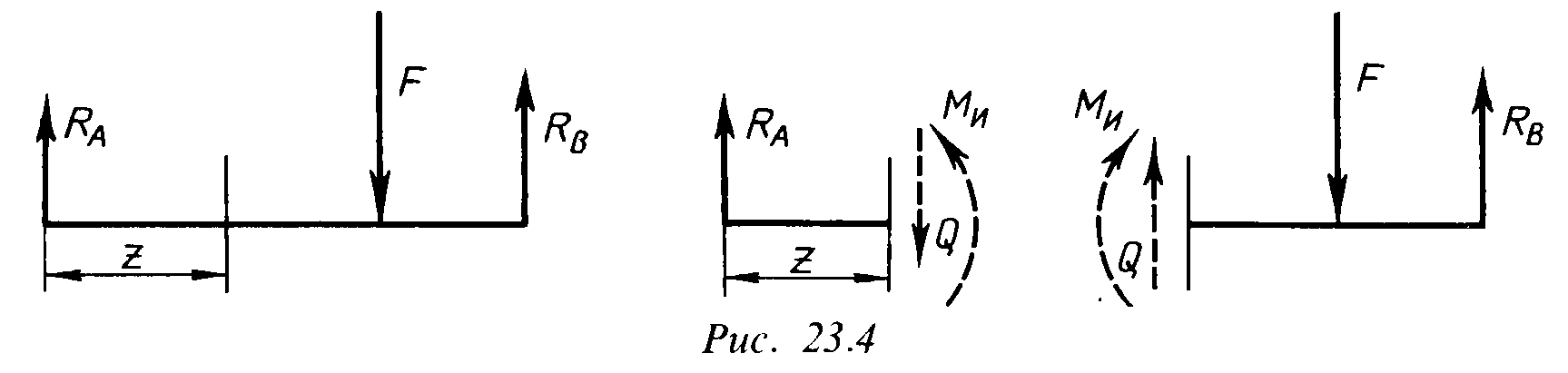
Рис. 2.
Рассматривая равновесие частей балки, расположенных слева и справа, видим, что в поперечных сечениях должны действовать изгибающий момент М и и поперечная сила Q. Из этого следует, что в рассматриваемом случае в точках поперечных сечений действуют не только нормальные напряжения, соответствующие изгибающему моменту, но и касательные, соответствующие поперечной силе.
Поперечная сила – это равнодействующая внутренних касательных сил в поперечном сечении балки.
Изгибающий момент в сечении балки численно равен алгебраической сумме моментов относительно центра тяжести сечения всех внешних сил, действующих справа или слева от сечения.
Поперечная сила в сечении балки численно равна алгебраической сумме всех внешних сил, действующих справа или слева от сечения.
Так как правила знаков статики неприемлемы для установления знаков изгибающего момента и поперечной силы, то установим для них другие правила знаков.
Правило определения знака для изгибающих моментов: если внешняя нагрузка стремится изогнуть балку выпуклостью вниз, то изгибающий момент в сечении считается положительным, и наоборот (рис. 3).
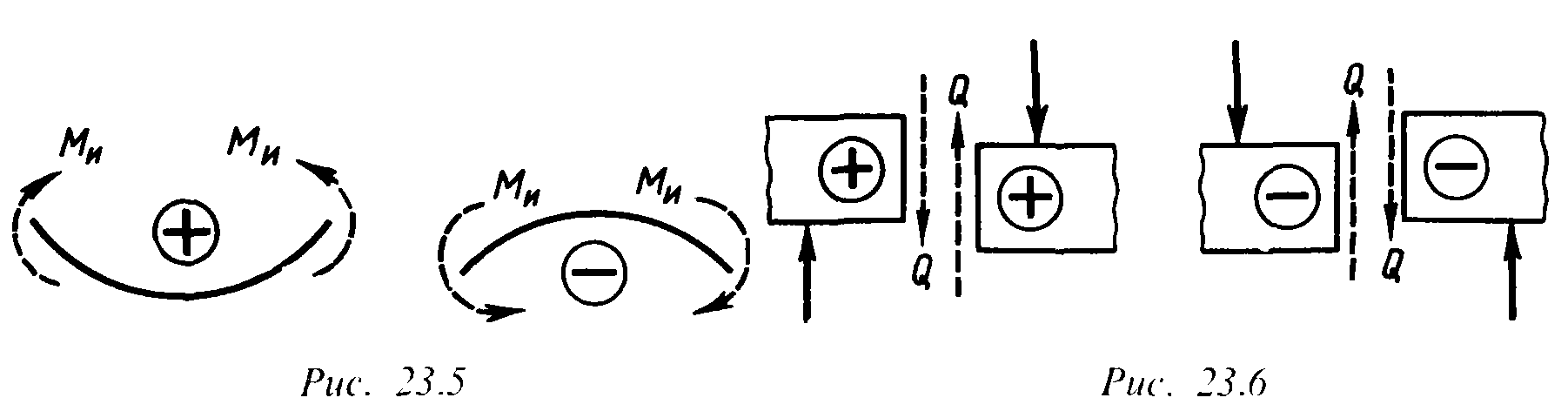
| |
| Рис. 3. | Рис. 4. |
Правило определения знака для поперечных сил: если сумма внешних сил, лежащих по левую сторону от сечения, дает равнодействующую, направленную вверх, то поперечная сила в сечении считается положительной, и наоборот; для части балки, расположенной справа от сечения, знаки поперечной силы будут противоположными (рис. 4).
Для определения опорных реакций пользуются правилами знаков статики; для определения знаков изгибающего момента и поперечной силы – правилами знаков сопротивления материалов.
Анализ внутренних силовых факторов начинается с определения полной системы внешних сил. Рассмотрим некоторые характерные примеры и установим правила определения изгибающих моментов и поперечных сил.
На рис. 5.показана простейшая двухопорная балка, нагруженная силой F.
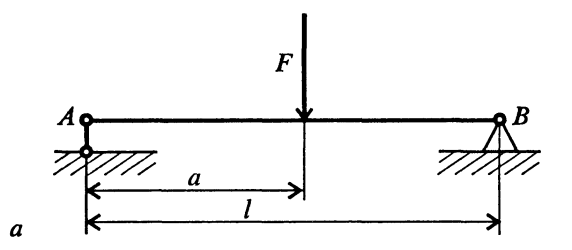
Рис. 5.
Освобождаем балку от связей и заменяем их действие реакциями (рис. 6).
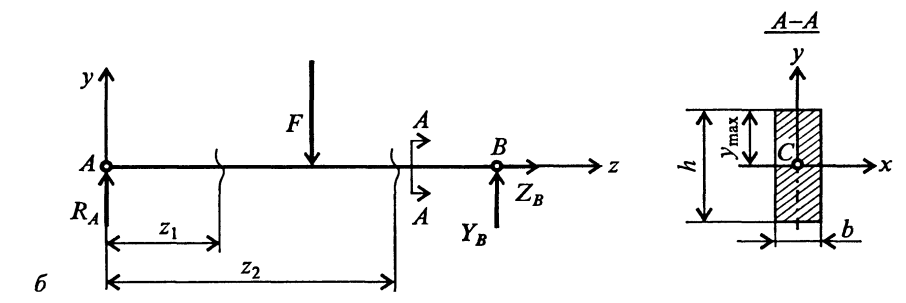
Рис. 6.
Опора А представляет собой невесомый стержень, поэтому реакция RА пойдет вдоль него.
В шарнире В реакцию раскладываем на две составляющие. Несмотря на то, что выбор системы координат, безусловно, произволен, в сопротивлении материалов принято ось z направлять вдоль бруса; оси х и у должны лежать в плоскости, перпендикулярной к этой оси, причем поворот от оси х к оси у должен происходить против хода часовой стрелки, если смотреть с конца оси z.
Составим уравнения равновесия для плоской системы сил и определим неизвестные реакции связей. Неизвестных величин три – RА, YВ, ZВ. Уравнений статики тоже три, следовательно, задача статически определимая:
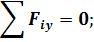
| 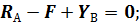
|
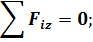
| 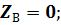
|
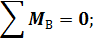
| 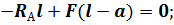
|
Отсюда находим реакции опор: ZB = 0; RA = F(l – a)/l; YB = Fa/l
Теперь приступим к выявлению внутренних силовых факторов в поперечных сечениях бруса. Для этого между точками приложения внешних сил и моментов, воспользовавшись методом сечений, составляют уравнения равновесия отсеченных частей. Так, в конкретном примере необходимо делать сечения дважды: на расстоянии z 1и z2 от левой опоры. На рис. 7.показано, как рассечен брус на расстоянии z 1.
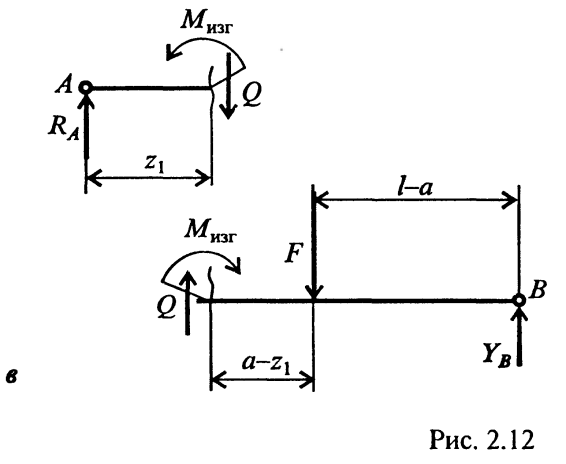
Рис. 7.
Следует обратить внимание на то, чтобы внутренние силовые факторы в поперечном сечении левой и правой частей были обязательно противоположны по направлению.
Из предыдущего материала уже известно, что внутренние силовые факторы определяются из уравнений равновесия отсеченных частей.
В сечении на расстоянии z 1от начала координат (т.е. в левой части бруса от сечения, см. рис. 7)поперечная сила Q имеет положительный знак и на эпюре будет откладываться вверх.
При рассмотрении равновесия правой отсеченной части для сил, лежащих справа от сечения, имеет место обратная зависимость.
Построение эпюр изгибающих моментов и поперечных сил осуществляется в следующей последовательности:
1) определяют реакции опор;
2) выявляют в поперечных сечениях бруса все внутренние силовые факторы (их значение и знак);
3) строят эпюры.
Построим эпюры для балки, представленной на рис. 7, используя полученные ранее вычисления.
1. Определяем реакции опор. Составляем уравнения равновесия плоскойсистемы сил: RA = F(l – a)/l; YB = Fa/l
2. Определяем внутренние изгибающие моменты в поперечных сечениях балки. Для этого рассматриваем равновесие отсеченной левой части (рис. 8):
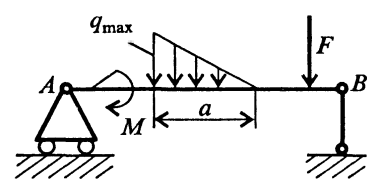
Рис. 8.
в сечении SMC(Fi) = 0; – RAz1 + Mизг = 0, откуда:
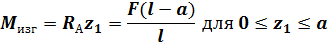
Всечении SMC(Fi) = 0; – RAz2 + F(z2 – a) + Mизг = 0;
Mизг = +RAz2 – F(z2 – a) дляа£z2£l
3. Определяем поперечные силы. В сечении z1 SFi= 0; RA– Q = 0
Отсюда Q = F(l – a)/l. В сеченииz2 SFi= 0; RA– F + Q = 0. Отсюда Q = F)/l
4. Строим эпюры изгибающих моментов.
Эпюра М изг в пределах 0 < z 1 < а имеет линейную зависимость. Задаемся z 1 = 0, при этом М изг = 0. Откладываем эту точку на эпюре (рис. 9). Далее при z 1= а
М изг = F(l-а)а/l.
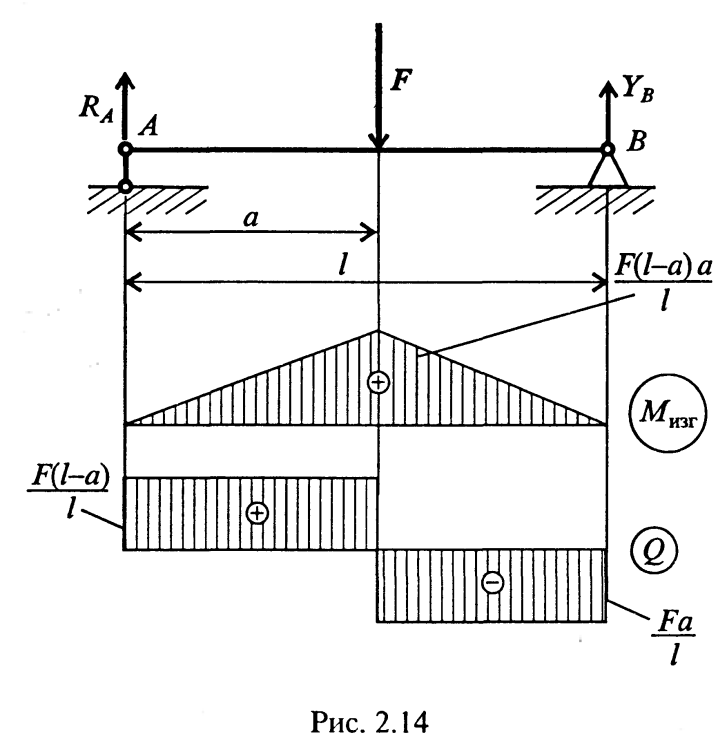
Рис. 9.
В пределах а <z2 <l получаем: при z2 = а
М изг = F(l-а)а/l;
при z2 = l
М изг= 0.
Откладываем эти ординаты (они построены на сжатом волокне) и соединяем линиями.
Следует заметить, что на втором участке можно было ординаты не вычислять, так как в шарнирной опоре В момент не может возникать, и поэтому на эпюре нужно сразу отложить 0.
5. Строим эпюры поперечных сил.
Как было выявлено в п. 3, поперечные силы постоянны на каждомиз двух участков, поэтому откладываем подсчитанные значения с учетом знаков. Нужно обратить внимание, что в точке приложения внешней силы должен быть скачок, равный приложенной силе.
На балку могут действовать сосредоточенные силы и моменты, а также распределенные по длине. Например, на рис. 8. F –сосредоточенная сила, М –сосредоточенный момент; на участке а приложена распределенная нагрузка от нуля до q mах.
Условие прочности балки при изгибе заключается в том, что максимальное нормальное напряжение в опасном сечении не должно превосходить допускаемое.
Полагая, что гипотеза о ненадавливании волокон справедлива не только при чистом, но и при поперечном изгибе, мы можем нормальные напряжения в поперечном сечении вычислять при поперечном изгибе по той- же формуле, что и при чистом изгибе.
Расчетная формула на прочность при изгибе имеет вид
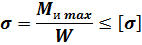
и читается так: нормальное напряжение в опасном сечении, вычисленное по формуле s = Ми mах/ W, не должно превышать допускаемое. Допускаемое нормальное напряжение при изгибе выбирают таким же, как и при растяжении и сжатии.
Максимальный изгибающий момент определяют из эпюр изгибающих моментов или расчетом.
Так как момент сопротивления изгибу W в расчетной формуле стоит в знаменателе, то, чем больше W, тем меньше будут расчетные напряжения.
Определим моменты сопротивления изгибу наиболее распространенных сечений:
1. Прямоугольник b х h (рис. 10):
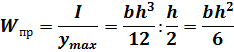
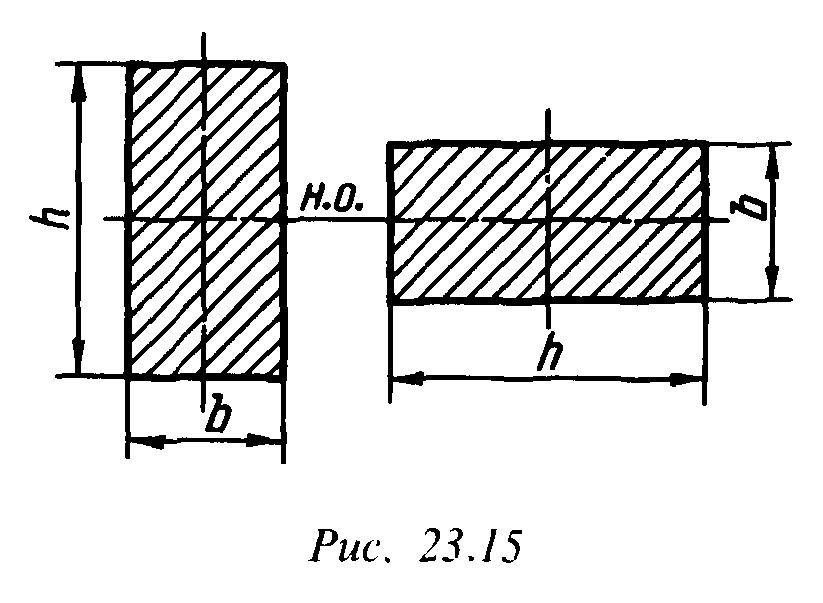
Рис.10.
Если балку прямоугольного сечения положить плашмя, то
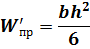
Тогда
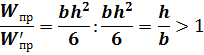
следовательно, при прочих равных условиях максимальные нормальные напряжения s' у прямоугольной балки, положенной плашмя, будут больше, чем у той же балки, когда ее наибольший габаритный размер h вертикален (имеется в виду, что изгиб происходит в вертикальной плоскости).
Из сказанного следует правило: для обеспечения максимальной прочности ось, относительно которой момент инерции максимален, должна быть нейтральной.
2.Кругдиаметром d:
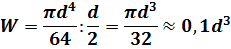
3. Круг размером D x d:
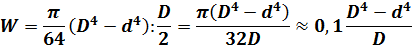
Момент сопротивления кольцевого сечения нельзя вычислять как разность моментов сопротивлений большого и малого кругов. Нетрудно подсчитать, что при одинаковой площади поперечного сечения, т. е. одинаковом расходе материала, момент сопротивления кольцевого сечения больше момента сопротивления сплошного круглого сечения.
Так как вблизи нейтральной оси материал мало напряжен, то выгодно больше материала располагать дальше от нейтральной оси. Поэтому в машиностроении редко применяют металлические балки прямоугольного сечения, но весьма широко распространены прокатные профильные балки таврового, двутаврового, углового, швеллерного и других сечений. Моменты инерции, моменты сопротивления и другие сведения о прокатных фасонных профилях стандартных размеров даются в таблицах ГОСТа.
Для балок, материал которых неодинаково работает на растяжение и сжатие (например, чугун), целесообразно применять профили, не симметричные относительно нейтральной оси, например тавровый или П-образный. Так как у несимметричного профиля при изгибе возникают неодинаковые напряжения растяжения и сжатия, то сечение, например, чугунной балки выгодно располагать так, чтобы меньшие напряжения были в зоне растянутых, а большие – в зоне сжатых волокон (рис. 11).
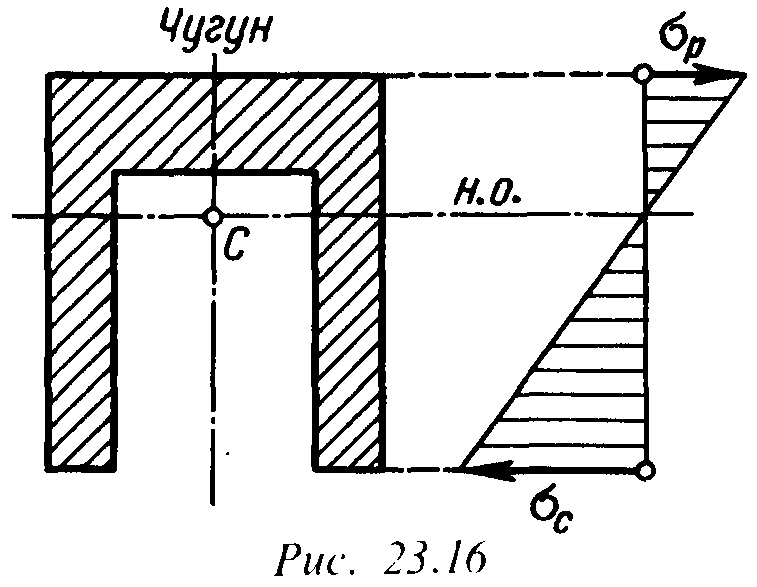
Рис. 11.
Литература: Эрдеди А.А.Теоретическая механика. Сопротивление материалов. §23.1-23.9. стр. 217-243