| Аксонометрические проекции |
Согласно ГОСТ 2.317-69, из прямоугольных аксонометрических проекций рекомендуется применять прямоугольные изометрию и диметрию.
В прямоугольной изометрии размеры предмета по всем трем измерениям сокращаются на 18 %. ГОСТ рекомендует изометрическую проекцию строить без сокращения по осям координат), что соответствует увеличению изображения против оригинала в 1,22 раза.
На рисунках 172 и 173 показано расположение осей в изометрии и диметрии.

Рисунок 172 - Расположение осей в изометрии

Рисунок 173 - Расположение осей в диметрии
При построении прямоугольной диметрической проекции сокращение длин по оси y' принимают вдвое больше, чем по двум другим. В практических построениях вводится масштаб увеличения, равный 1,06, и тогда коэффициенты искажения по осям x' и z' равны единице, а по оси y' вдвое меньше - 0,5.
| Построение окружности в аксонометрии |
При параллельном проецировании окружности на какую-нибудь плоскость П* получаем ее изображение в общем случае в виде эллипса (рисунок 174).

Рисунок 174 - Проецирование окружности на плоскость
ГОСТ 2.317-69 определяет положение окружностей, лежащих в плоскостях, параллельных плоскостям проекций для прямоугольной изометрической проекции (рисунок 175) и для прямоугольной диметрии (рисунок 177).

Рисунок 175 - Изометрические проекции окружностей расположенных в
плоскостях параллельных плоскостям проекций
Построение изометрической проекции окружности показано на рисунке 176. Если изометрическую проекцию выполняют без искажения по осям x, y, z, то большая ось эллипсов 1,2, 3 равна 1,22, а малая ось - 0.71 диаметра окружности. Если изометрическую проекцию выполняют с искажением по осям x, y, z, то большая ось эллипсов 1, 2, 3 равна диаметру окружности, а малая - 0.58 диаметра окружности.

Рисунок 176 - Построение изометрической проекции окружности
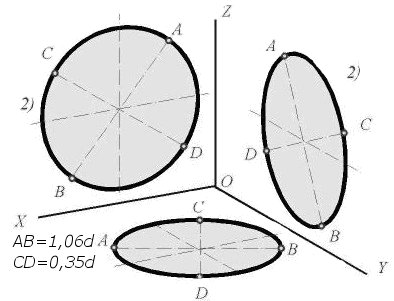
Рисунок 177 - Диметрические проекции окружностей расположенных в
плоскостях параллельных плоскостям проекций
Построение диметрической проекции окружности представлено на рисунке 178. Если диметрическую проекцию выполняют без искажения по осям x и z то большая ось эллипсов 1, 2, 3 равна 1,06 диаметра окружности, а малая ось эллипса 1 - 0.95, эллипсов 2 и 3 - 0.35 диаметра окружности. Если диметрическую проекцию выполняют с искажения по осям x и z, то большая ось эллипсов 1, 2, 3 равна диаметру окружности, а малая ось эллипса 1 - 0.9, эллипсов 2 и 3 - 0,33 диаметра окружности.
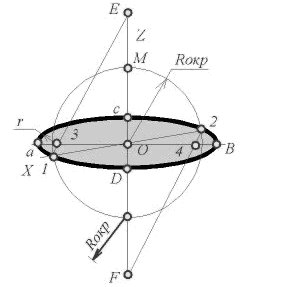
Рисунок 178 - Построение диметрической проекции окружности
Как бы ни была расположена плоскость окружности, сначала целесообразно построить параллелограмм A*B*C*D* – параллельную проекцию квадрата ABCD, описанного около данной окружности, а затем с помощью восьми точек и восьми касательных вписать в него эллипс. Точки 1, 3, 5 и 7 – середины сторон параллелограмма. На отрезке 3*B*, как на гипотенузе, построить прямоугольный равнобедренный треугольник 3*KB*; из точки 3* радиусом 3*K описать полуокружность, которая пересечет A*B* в точках L и M; эти точки делят отрезок 3*A* и равный ему отрезок 3*B* в отношении 3:7; через точки L и М провести прямые параллельные боковым сторонам параллелограмма, и отметить точки 2*, 4*, 6* и 8* расположенные на диагоналях. Построить касательные к эллипсу в найденных точках. Касательные t 2 и t 6 параллельны BD, а касательные t 4 и t 8 параллельны AC. Получив восемь точек и столько же касательных, можно с достаточной точностью вычертить эллипс (рисунок 179).

Рисунок 179 - Построение эллипса
| Построение аксонометрических изображений |
Переход от ортогональных проекций предмета к аксонометрическому изображению рекомендуется осуществлять в такой последовательности:
На ортогональном чертеже размечают оси прямоугольной системы координат, к которой и относят данный предмет. Оси ориентируют так, чтобы они допускали удобное измерение координат точек предмета. Например, при построении аксонометрии тела вращения одну из координатных осей целесообразно совместить с осью тела (рисунок 180)

Рисунок 180 - Построение аксонометрического изображения
2. Строят аксонометрические оси с таким расчетом, чтобы обеспечить наилучшую наглядность изображения и видимость тех или иных точек предмета.
3. По одной из ортогональных проекций предмета чертят вторичную проекцию.
4. Создают аксонометрическое изображение, для наглядности делают вырез четверти.
| Штриховка в аксонометрии |
Согласно ГОСТ 2.317-68 ЕСКД линии штриховки сечений в аксонометрических проекциях наносят параллельно одной из диагоналей проекций квадратов, лежащих в соответствующих координатных плоскостях, стороны которых параллельны аксонометрическим осям (рисунок 181).

Рисунок 181 - Штриховка в аксонометрии
При нанесении размеров выносные линии проводят параллельно аксонометрическим осям, размерные линии – параллельно измеряемому отрезку.
В аксонометрических проекциях спицы маховиков и шкивов, ребра жесткости и подобные элементы штрихуют.
Сечение - это фигура, полученная при мысленном рассечении предмета плоскостью. Сечение отличается от разреза тем, что в разрезах изображается то, что находится в сечении, и то, что находится за сечением. В сечениях изображается только то, что находится в сечении. Сечения,не входящие в состав разреза, разделяют на вынесенные и наложенные.
Метод проецирования
Проецирование — это процесс получения проекций предмета на какой-либо поверхности (плоской, цилиндрической, сферической, конической) с помощью проецирующих лучей.
Проецирование может осуществляться различными методами.
Методом проецирования называется способ получения изображений с помощью определенной, присущей только ему совокупности средств проецирования (центра проецирования, направления проецирования, проецирующих лучей, плоскостей (поверхностей) проекций), которые определяют результат — соответствующие проекционные изображения и их свойства.
Для того чтобы получить любое изображение предмета на плоскости, необходимо расположить его перед плоскостью проекций и из центра проецирования провести воображаемые проецирующие лучи, пронизывающие каждую точку поверхности предмета. Пересечение этих лучей с плоскостью проекций дает множество точек, совокупность которых создает изображение предмета, называемое его проекцией. Это общее определение рассмотрим на примере проецирования точки, прямой, треугольника и треугольной призмы на плоскость проекций H.
Существует центральное (или перспективное) и параллельное проецирование. Параллельное проецирование бывает прямоугольным (ортогональным) или косоугольным (табл. 5).
Методы проецирования

Центральное проецирование (перспектива) характеризуется тем, что проецирующие лучи исходят из одной точки (S), называемой центром проецирования. Полученное изображение называется центральной проекцией.
Перспектива передает внешнюю форму предмета так, как воспринимает его наше зрение.
При центральном проецировании, если предмет находится между центром проецирования и плоскостью проекций, размеры проекции будут больше оригинала; если предмет расположен за плоскостью проекций, то размеры проекции станут меньше действительных размеров изображаемого предмета.
Параллельное проецирование характеризуется тем, что проецирующие лучи параллельны между собой. В этом случае предполагается, что центр проецирования (S) удален в бесконечность.
Изображения, полученные в результате параллельного проецирования, называются параллельными проекциями.
Если проецирующие лучи параллельны между собой и падают на плоскость проекций под прямым углом, то проецирование называется прямоугольным (ортогональным), а полученные проекции — прямоугольными (ортогональными). Если проецирующие лучи параллельны между собой, но падают на плоскость Проекций под углом, отличным от прямого, то проецирование называется косоугольным, а полученная проекция — косоугольной. При проецировании объект располагают перед плоскостью проекций таким образом, чтобы на ней получилось изображение, несущее наибольшую информацию о форме.