1. Чтобы ответить на поставленные вопросы, необходимо найти опасный участок вала, т.е. участок с наибольшим крутящим моментом.
2. Условие прочности и условие жесткости выражаются формулами (3.4) и (3.5), соответственно.
3. Для определения максимального крутящего момента 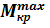 необходимо из условия равновесия:
необходимо из условия равновесия:
 (3.6)
(3.6)
определить величину и направление неизвестного крутящего момента M0.
Для этого необходимо вал разбить на участки. Границами участков являются сечения, в которых приложены крутящие моменты (в настоящем задании расчетная схема состоит из 4- х участков).
4. Начинать рассматривать вал можно с любой стороны с учетом знака каждого крутящего момента. (крутящий момент считается положительным, если при рассматривании со стороны сечения он действует против хода часовой стрелки и наоборот).
5. Используя метод сечений, вычислить величину крутящего момента на каждом участке (величина крутящего момента на каждом участке равна сумме крутящих моментов, действующих по одну сторону от сечения).
6. По полученным результатам необходимо построить эпюру крутящих моментов по длине вала и определить наиболее опасный участок (участок, где действует  ).
).
7. Определить диаметр вала из условия прочности (3.4).
8. На каждом участке вычислить относительнный угол закручивания и сравнить с допускаемым [ Ө ].
9. При необходимости вычислить диаметр вала из условия жесткости.
10. Построить эпюру углов закручивания.
Вопросы для самопроверки
1. Что называется абсолютным и относительным сдвигом?
2. Как формулируется закон Гука при сдвиге?
3. Что характеризует модуль упругости II рода?
4. Запишите формулу условия прочности заклепочного соединения.
5. Какие напряжения возникают в поперечных сечениях круглого вала при кручении?
6. Как производится расчет вала на прочность при кручении?
7. Как строятся эпюры крутящих моментов и углов закручивания?
8. В чем разница между абсолютным и относительным углом закручивания?
9. Как производится расчет вала на жесткость при кручении?
Тема 4. Поперечный изгиб прямого бруса
Эта тема является самой большой и самой сложной, ее следует изучать постепенно.
Изгиб ‒ вид деформации, при котором происходит изменение кривизны продольных осей брусьев. Изгиб связан с возникновением в поперечных сечениях бруса изгибающих моментов и поперечных сил..
Если при изгибе в поперечном сечении бруса действует только изгибающий момент Мx, то соответственно имеется чистый изгиб. Если в поперечном сечении действует также и поперечная сила Qy, то имеется поперечный изгиб.
Прямой изгиб бруса возникает в случае, когда изгибающий момент в данном поперечном сечении бруса действует в плоскости, проходящей через одну из главных центральных осей инерции этого сечения. В случае, когда плоскость действия изгибающего момента в данном поперечном сечении бруса не проходит ни через одну из главных осей инерции этого сечения, изгиб называется косым.
Таким образом, кривизна изогнутой оси балки связана с изгибающим моментом выражением:
{\displaystyle {\frac {1}{\rho }}={\frac {M_{x}}{EJ_{x}}}}  (4.1)
(4.1)
Распределение нормальных напряжений по высоте сечения выражается формулой:
{\displaystyle \sigma ={\frac {M_{x}}{J_{x}}}y} 
 · y (4.2)
· y (4.2)
{\displaystyle W_{x}={\frac {bh^{2}}{6}}}
{\displaystyle W_{x}={\frac {bh^{2}}{6}}}Максимальное напряжение в сечении выражается формулой:
{\displaystyle \sigma _{max}={\frac {M_{x}}{J_{x}}}{\frac {h}{2}}={\frac {M_{x}}{W_{x}}}} 
 σmax =
σmax =  ·
·  =
= 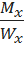 , (4.3)
, (4.3)
{\displaystyle W_{x}={\frac {bh^{2}}{6}}}где {\displaystyle W_{x}={\frac {J_{x}}{\frac {h}{2}}}} ρ ‒ радиус изгиба продольной оси бруса; Ix ‒ момент инерции поперечного сечения бруса; Wx ‒ момент сопротивления сечения изгибу; h ‒ {\displaystyle h} высота сечения балки.
Величины {\displaystyle J_{x}}Ix и {\displaystyle W_{x}}Wx для простых сечений (круглое, прямоугольное) вычисляются аналитически. Для круглого сечения диаметром {\displaystyle d}d:
Ix =  ; Wx =
; Wx =  (4.4)
(4.4)
{\displaystyle J_{x}={\frac {\pi d^{4}}{64}}}{\displaystyle W_{x}={\frac {\pi d^{3}}{32}}}Для прямоугольного сечения высотой h {\displaystyle h} и шириной {\displaystyle b} b:
{\displaystyle J_{x}={\frac {bh^{3}}{3}}}  Ix =
Ix = 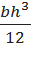 ; Wx =
; Wx =  (4.5)
(4.5)
{\displaystyle W_{x}={\frac {bh^{2}}{6}}}Для более сложных сечений (швеллер, двутавр), имеющих стандартные размеры, эти величины приведены в справочной литературе.Надо ясно представлять пути увеличения момента сопротивления сечения без увеличения расхода материала.
Изгибающий момент в сечении может быть получен методом сечений.
Для наглядного представления о законах изменения поперечной силы Qу и изгибающего момента Мx по длине балки удобно изображать их в виде графиков (эпюр), ординаты которых соответствуют значениям поперечных сил и изгибающих моментов в любом ее сечении.
Построение эпюр производится следующим образом.
Линию, параллельную оси балки (ось Z), принимают за ось абсцисс (нулевая линия), от которой в произвольном масштабе откладывают ординаты, соответствующие значениям Qу или Мх в различных сечениях балки. Соединяя концы отложенных ординат, получаем эпюры Qу и Мx, соответственно.
Ординаты, выражающие величины положительных Qу и Мx, принято откладывать вверх от оси Z, а отрицательных – вниз (студенты строительных специальностей положительные величины изгибающих моментов откладывают вниз).
Штриховать эпюры следует только вертикальными линиями, поскольку каждая линия штриховки в принятом масштабе выражает величину Qу или Мх в данном сечении. Рекомендуется проверять правильность построения эпюр, используя дифференциальную зависимость между Qу и Мx.
Порядок выполнения работы:
1. Определяют опорные реакции балки.
2. Обозначают характерные сечения (точки) балки. Ими являются: концевые сечения балки, опоры, точки приложения сосредоточенных сил и моментов, начало и конец распределенной нагрузки.
3. Для построения эпюры поперечных сил Qу определяют значения поперечных сил в характерных точках.
Необходимо помнить, что:
Поперечная сила в сечении равна сумме проекций всех сил, расположенных по одну сторону от сечения, на ось ординат (ось Y), которая перпендикулярна к оси элемента.
Сила, расположенная слева от рассматриваемого сечения и направленная вверх, считается положительной, а сила, направленная вниз, – отрицательная, для правой части балки знаки меняются наоборот (Рис.4.1а).
Найденные значения поперечных сил в характерных точках отложим в масштабе от нулевой линии. Эти значения соединяем соответствующими линиями, руководствуясь правилами:
а) если на участке балки распределенная нагрузка отсутствует (q =0), то под этим участком Qу = const и эпюра представляет собой прямую, параллельную нулевой линии;
б) если на участке балки приложена распределенная нагрузка, причем q =const, то под этим участком поперечная сила меняется по линейному закону.
Соединив все значения поперечных сил по указанным правилам, получим эпюру Qу.

а)

б)
Рис.4.1 Знаки поперечных сил а) и изгибающих моментов б) при изгибе
4. Для построения эпюры изгибающих моментов Мх определяем изгибающие моменты в характерных сечениях.
Необходимо помнить, что:
изгибающий момент в рассматриваемом сечении равен сумме моментов от всех сил (распределенных, сосредоточенных, в том числе и опорных реакций), а также внешних сосредоточенных моментов, расположенных по одну сторону от сечения.
Если любое из перечисленных силовых воздействий стремится повернуть левую часть балки относительно рассматриваемого сечения по часовой стрелке, то они образуют положительный изгибающий момент, а если противчасовой стрелки – отрицательный изгибающий момент. Для правой части – наоборот (рис.4.1б).
Полученные значения откладывают в масштабе от нулевой линии. Соединяют концы отложенных ординат, руководствуясь следующими правилами:
а) если на участке нет распределенной нагрузки (q =0), то на этом участке изгибающий момент меняется по линейному закону (концы отложенных ординат соединяются прямой линией);
б) если на участке балки отсутствует поперечная сила (Qу =0), то на этом участке Мх = const;
в) на участке балки, где приложена распределенная нагрузка, изгибающий момент изменяется по параболе. Парабола имеет выпуклость навстречу действия нагрузки, т.е. при действии нагрузки сверху вниз парабола обращена выпуклостью вверх;
г) если эпюра Qу на рассматриваемом участке не пересекает нулевую линию, то эпюра Мх может быть построена по двум точкам, так как все значения изгибающих моментов в промежуточных сечениях участка находятся между значениями в характерных сучениях (на границах участка);
д) если эпюра Qу пересекает нулевую линию (меняет знак), то под этим сечением эпюра Мх будет иметь экстремум (максимальное или минимальное значение) или вершину параболы. Положение этого сечения находят по эпюре Qу (из подобия треугольников определяют координату сечения, где Qу =0). Затем находят значение изгибающего момента в этом сечении и строят эпюру Мх на участке с распределенной нагрузкой по трем точкам.
Соединив все полученные точки по указанным выше правилам, получают график изменения изгибающих моментов по длине балки. Этот график называется эпюрой Мх.
Методику построения эпюр Qу и Мх рассмотрим на конкретном примере:
Пример. Построить эпюры Q у и Мх для балки, изображенной на рис. 4.2.
Решение:
1) используя уравнения равновесия, определяем опорные реакции балки:
Σ МА = 0 МА = Р(а+b)+q  – q
– q  +VВ(c+d)+M = 0,
+VВ(c+d)+M = 0,
Откуда: VВ =  = 26,4кН
= 26,4кН

Рис.4.2 Пример построения эпюр поперечных сил и изгибающих моментов для балки, работающей на изгиб.
Σ МВ = 0 МВ = Р(а+b+с+d)+q(b+c)(  +d) – VA(c+d)+M = 0,
+d) – VA(c+d)+M = 0,
Откуда: VA = 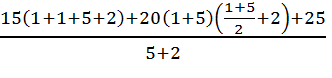 = 108,6кН
= 108,6кН
Проверка: ΣРу = 0 –15–20(1+ 5) +108,6 +26,4 = 0
Построение эпюры Q:
QC = QD = – P = – 15кН;
QA лев = – P – qb= – 15– 20·1= – 35кH;
QAправ = – VB + qc = – 26,4 + 20·5 = 73,6кН;
QE =QB лев = – VB = – 26,4кН;
QB прав = QК = 0
Строим эпюру Qу, откладывая положительные значения ординат вверх от оси Z, а отрицательные - вниз (рис.4.2б).
Из графических построений видно, что на участке АЕ эпюра Qy пересекает продольную ось балки в точке R. Из подобия треугольников, образовавшихся на этом участке эпюры Qy (с = 5 м), определим расстояние z0 от левой опоры до сечения, в котором Q = 0, т.е. решаем пропорцию:

Расчет показывает: z0 = 3,68м.
Построение эпюры Мx.
Составляем уравнения изгибающих моментов по каждому участку.
Участок I
Проводим сечение 1-1 на расстоянии z 1 от начала координат (точка С).
Изгибающий момент М 1 определяем по выражению:
М 1 = –Р· z1,где 0 ≤ z 1 ≤ a
Уравнение показывает, что на участке I наблюдается линейная зависимость М1 от z1, при этом: МС = 0, MD = –15кНм.
Участок II
Проводим сечение 2-2 на расстоянии z 2 от начала координат.
Изгибающий момент М2 определяем по выражению:
М 2 = –Р· z 2 – q  , где a ≤ z2 ≤ (a + b)
, где a ≤ z2 ≤ (a + b)
Величина изгибающего момента:
- в (·) D (при z 2 = a = 1м) МD = –15кНм;
- в(·) А (при z 2 = a+b = 2м) MA = – 40кНм
При этом наблюдается параболическая зависимость М2 от z2.
Участок III
Проводим сечение 3-3 на расстоянии z 3 от начала координат.
Изгибающий момент М3 определяем по выражению:
М 3 = –Р· z 3 – q  +VA (z 3 – (a+b),где (a+b) ≤ z 3 ≤ (a+b+c)
+VA (z 3 – (a+b),где (a+b) ≤ z 3 ≤ (a+b+c)
Величина изгибающего момента:
- в(·) А (при z 3 = a+b = 2м) MA = – 40кНм
- в (·) R (при z 3 = a+b+ z 0 = 5,68м) МR = 95,4кНм – экстремум;
- в (·) Е (при z 3 = a+b+с = 7м) МЕ = 78кНм
Участок IV
Для упрощения вычислений участок IV будем рассматривать справа (по схеме). Для этого проводим сечение 4-4 на расстоянии z4 от начала координат (точка К).
Изгибающий момент М 4 определяем по выражению:
М4 = М+VВ ( z4 – e), где e ≤ z4 ≤ (e+d)
Величина изгибающего момента:
- в(·) B (при z 4 = e = 1,5м) MB = 25кНм;
- в (·) E (при z 4 = e+d = 3,5м) МE = 78кНм
При этом наблюдается линейная зависимость М 4 от z4.
Участок V
Проводим сечение 5-5 на расстоянии z5 от начала координат (точка К).
Изгибающий момент М5 определяем по выражению:
М 5 = М,где 0 ≤ z 5 ≤ e
Уравнение показывает, что изгибающий момент не зависит от координаты сечения на участке V и равен по величине сосредоточенному моменту, приложенному в (·) К.
Такимобразом:
- в(·) B (при z 4 = e = 1,5м) МК = MB = М =25кНм;
- в (·) E (при z 4 = e + d = 3,5м) МE = 78кНм
При этом наблюдается линейная зависимость М 4 от z4.
Анализ эпюр показывает, что наиболее нагруженное сечение балки находится в точке R (Mmax = 95,4 кНм).
Вопросы для самопроверки
1. Какой вид деформации называется поперечным изгибом?
2. Условия возникновения чистого изгиба?
3. Какие напряжения возникают в поперечных сечениях бруса (балки) при чистом изгибе?
4. Какие напряжения возникают в поперечных сечениях бруса (балки) при поперечном изгибе?
5. Как распределяются нормальные напряжения по высоте поперечного сечения при изгибе?
6. Как распределяются касательные напряжения по высоте поперечного сечения при изгибе?
7. Как производится расчет бруса (балки) на прочность при изгибе?
8. Как строятся эпюры поперечных сил и изгибающих моментов?
9. Как производится расчет бруса (балки) на жесткость при изгибе?
10. Какова дифференциальная зависимость между распределенной нагрузкой q, перечной силой Qy и изгибающим моментом Мх ?
Список литературы
1. Феодосьев В.И. Сопротивление материалов. Главная редакция физико – математической литературы изд-ва «Наука», 1974.- 560 с.
2. Степин П.А. Сопротивление материалов: учебник / П.А. Степин.-11-е изд.,- СПб.: Лань, 2010.-319 с.
3. Сопротивление материалов: Пособие по решению задач.- 8-е изд.- СПб.: Лань, 2009.-508с.:ил.
4. Сопротивление материалов: учеб.- метод. Пособие. Ч.1/ авт. сост. П.П. Болдышев, Н.Р. Виснап; НовГУ им. Ярослава Мудрого.- Великий Новгород, 2009.-111с.
5. Сопротивление материалов: учеб.- метод. Пособие. Ч.2 / авт. сост. П.П. Болдышев, Н.Р. Виснап; НовГУ им. Ярослава Мудрого.- Великий Новгород, 2009.-71с.
Приложение 1