Тема 2. Осевое растяжение (сжатие)

СОПРОТИВЛЕНИЕ МАТЕРИАЛОВ

 

Методические указания и варианты контрольных заданий

для студентов заочной формы обучения по направлениям подготовки:

Строительство»

Профиль ”Промышленное и гражданское строительство”

Конструкторско - технологическое обеспечение машиностроительных производств»

Профиль ” Технология машиностроения”

 

ВЕЛИКИЙ НОВГОРОД

Печатается по решению

кафедры

 

Сопротивление материалов: методические указания и варианты контрольных заданий для студентов заочной формы обучения по направлениям подготовки: 08.03.01 «Строительство»; 15.03.05 «Конструкторско - технологическое обеспечение машиностроительных производств» / авт. сост. О. В. Летенков; НовГУ им. Ярослава Мудрого, – Великий Новгород, 2018. – 37с.

 

 

Методические указания содержат краткие теоретические сведения по темам курса, список контрольных вопросов для самопроверки, варианты контрольных заданий и рекомендуемую литературу.

Приведены требования к оформлению контрольных работ.

Предназначено для студентов заочной формы обучения по направлениям подготовки 08.03.01. «Строительство». Профиль ”Промышленное и гражданское строительство”; 15.03.05. «Конструкторско- технологическое обеспечение машиностроительных производств». Профиль” Технология машиностроения”

 

 

Новгородский государственный

университет, 2018

О. В. Летенков

СОДЕРЖАНИЕ

Стр.

Введение………………………………………………....…….…4

Методические указания по темам курса……………….……..…5

Тема 1. Основные понятия и определения……………….…….5

Тема 2. Осевое растяжение (сжатие) КР№1………………….….6

Тема 3. Сдвиг и кручение (КР№2)…………………. ………..…11

Тема 4. Прямой изгиб (КР№3)……………………………..……14

Список литературы…………………………………………..…...21

Приложения…………………………………………………….....22

\

ВВЕДЕНИЕ

 

Сопротивление материалов является одной из наиболее сложных дисциплин в высших учебных заведениях, поэтому при изучении курса рекомендуется вести конспект с кратким изложением теоретического материала и решением типичных задач, рассматриваемых на лекционных и практических занятиях по каждому разделу.

Совершенно необходимо научиться решать задачи самостоятельно. Курс «Сопротивление материалов» дает методику решения наиболее типичных задач.

Представленные методические указания составлены в соответствии с программой учебного модуля по сопротивлению материалов.

Студент заочной формы обучения выполняет три контрольных работы. Варианты заданий выбираются по двум последним цифрам зачетной книжки (если №_вар ˃30, то выбирается последняя цифра).

 

 

Основные требования при выполнении

контрольных работ

 

►контрольные работы выполняются либо на пронумерованных листах, сшитых в тетрадь формата А4 (титульный лист выполняется по форме, приведенной в Приложении 1), либо в учебных тетрадях с полями (≈5см) для замечаний преподавателя;

► варианты контрольных работ приведены в Приложении 2;

► вся графическая часть выполняется аккуратно и в масштабе;

► на первой странице должно быть поставлено условие задачи и выполнен рисунок со всеми необходимыми размерами и величинами нагрузок;

► текстовая часть с необходимыми расчетами и дополнительные рисунки, разъясняющие решение задачи, приводятся в произвольной форме c соответствующими пояснениями;

► все физические величины приводить в соответствии с международной системой единиц (СИ)

 

МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ТЕМАМ КУРСА

Тема 1. Основные понятия и определения

Дисциплина «Сопротивление материалов» изучает расчет конструкций на прочность, жесткость и устойчивость при различных видах напряженного состояния.

Для выполнений этих расчетов сначала определяют внутренние силовые факторы, возникающие в поперечных сечениях конструкции под действием внешних сил.

При изучении темы необходимо понять сущность метода сечений, обратить внимание на понятия напряжение и деформация.

Напряжение является мерой внутренних сил, возникающих в теле под действием внешних нагрузок.

Деформация является мерой изменения формы и размеров тела (части тела), возникающих в теле под действием внешних нагрузок, температуры, влажности и пр.

Важно знать, что закон Гука справедлив только в области упругих деформаций. Необходимо понимать запись закона Гука, как в абсолютных, так и относительных единицах.

Сущность метода сечений заключается в том, что тело (элемент конструкции) в интересующем нас месте мысленно рассекается на две части. Одну из частей удаляют, а действие удаленной части на оставшуюся заменяют равнодействующей внутренних сил, возникающих в этом сечении. Таким образом, внутренние силы переходят в разряд внешних сил.

Поскольку все тело находится в равновесии, то и оставшаяся часть также будет находиться в состоянии равновесия, что позволяет составить соответствующие уравнения равновесия и определить равнодействующую внутренних сил.

 

Вопросы для самопроверки

1. Какие бывают силы?

2. Что такое напряжение?

3. Что такое деформация?

4. Какие деформации называются упругими?

5. Какие деформации называются пластическими?

6. В чем состоит сущность метода сечений?

Тема 2. Осевое растяжение (сжатие)

В этой теме следует обратить внимание на определение механических характеристик (предел пропорциональности, предел прочности, предел упругости и предел текучести). При этом важно оценить способность материала сопротивляться действию внешних сил.

Пользуясь формулами закона Гука, надо помнить, что этот закон справедлив только в пределах упругих деформаций.

Растяжение и сжатие характеризуются возникновением в поперечных сечениях внутренних сил N.

Центральным растяжением (сжатием) называется такой вид деформации, при котором в любом поперечном сечении бруса возникает только продольная сила N, а остальные силовые факторы равны нулю.

Явление центрального растяжения (сжатия) возникает в случае, когда все внешние нагрузки действуют по оси, проходящей через центры тяжести поперечных сечений бруса.

1. Внутренние силы N определяют методом сечений. Для этого брус рассекают на отдельные участки, отбрасывают одну из частей, а ее влияние на оставшуюся часть заменяют неизвестной внутренней силой N.

Для каждого сечения составляется уравнение равновесия:

ΣF+N=0, (2.1)

где ΣF – сумма всех внешних сил, находящихся по одну сторону от сечения; N– продольная сила в сечении (внутренняя сила).

Решением уравнения (2.1) определяют величину N.

Для наглядного представления характера (закона) изменения какого-либо из внутренних силовых факторов по длине бруса строят эпюру.

Эпюры представляют собой графики, продольной осью которых является ось бруса, а ординатами – значения определяемых величин (N, σ, ∆l).

2. В поперечных сечениях бруса при центральном растяжении (сжатии)

возникают равномерно распределенные нормальные напряжения σ, равные отношению внутренней продольной силы N к площади A поперечного сечения:

(2.2)

Нормальные напряжения при растяжении принимаются положительными, а при сжатии – отрицательными.

Условие прочности в этом случае будет определяться по выражению:

, (2.3)

где – внутреннее усилие на i – том участке, – площадь поперечного сечения i – того участка, – допускаемое нормальное напряжение.

Отсюда:
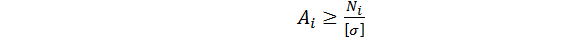(2.4)

3. Под действием растягивающих сил длина l стержня увеличивается на ∆l, а поперечные размеры его уменьшаются. По закону Гука удлинение стержня определяется по формуле:

Δ l ,(2.5)

где ∆l – абсолютное удлинение стержня, l – первоначальная длина стержня, Е – модуль упругости I-го рода.

Последовательность выполнения КР1 разберем на примере:

Пример. Для стального стержня (рис.1) определить во всех сечениях продольную силу N и нормальное напряжение σ. Определить вертикальные перемещения δ для всех поперечных сечений и полное удлинение Δl стержня. Результаты изобразить графически, построив эпюры N, σ и δ. Модуль продольной упругости материала стержня Е=2ž10⁵МПа.

Стержень жестко защемлен вверху и нагружен двумя внешними сосредоточенными силами F₁ =150кН, F₂ =200кН, приложенными в точках А и С и направленными вдоль его продольной оси. Площади поперечных сечений стержня А₁ =18см² и А₂ =12см².

Рис.1 Пример выполнения графической части КР1

Решение:

Разобьём стержень на отдельные участки, начиная со свободного конца. Границами участков считаются сечения, в которых приложены внешние силы, или меняются площади поперечных сечений.

В нашем случае наблюдаются следующие участки:

- участок АВ – участок от точки приложения силы F₁ (точка А) до сечения, в котором меняется площадь поперечного сечения (точка В).

- участок ВС – от точки В до сечения, где приложена сила F₂ (точка С).

- участок СД – от точки приложения силы F₂ до верхней опоры (точка D – точка подвеса).

Для определения внутреннего усилия N мысленно разрезаем стержень по сечениям I–I, II–II и III – III.

Из условия равновесия части стержня ниже сечения I–I (рис.1б) получим:

N₁ – F₁= 0, откуда N₁=F₁ =150кН (растяжение)

Из условия равновесия части стержня ниже сечения II–II (рис.1в) получим:

N₂ – F₁= 0, откуда N₂=F₁ =150кН (растяжение)

Из условия равновесия части стержня ниже сечения III–III (рис.1г) получим:

N₃+F₂ – F₁= 0, откуда N₃=F₁ – F₂ = 150 –200= –50кН (сжатие)

Зная продольную силу на каждом из трёх участков, определяем значения нормальных напряжений:

σ₁ = = = 8,33ž10³ = 83,3 ·10⁶ = 83,3МПа

σ₂ = = = 12,5ž10³ = 125 МПа

σ₃ = 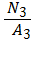= = – 4,17ž10³ = – 41,7МПа

По найденным значениям N и σ строим (в масштабе) эпюры продольных сил (рис.1д) и нормальных напряжений (рис.1е).

 

Из построений видно, что:

– эпюра продольных сил всегда имеет скачки в сечениях, где приложены или внешние силы, или расположены опоры. Причем, величина скачка равна или величине внешней силы, или величине реакции опоры;

– эпюра интенсивности нормальных напряжений всегда имеет скачки не только в сечениях, в которых приложены сосредоточенные силы (где имеет скачки эпюра продольных сил), но и в местах изменения площади поперечного сечения бруса;

– наиболее опасным является участок ВС, поскольку на этом участке действуют максимальные нормальные напряжения(σ₂ = 125 МПа).

Эпюры штрихуются линиями перпендикулярными к нулевой линии. В этом случае длина штрихов определяет в масштабе величину продольной силы или напряжения в соответствующем сечении бруса.

Для определения полного удлинения стержня находим перемещения характерных точек (А, В и С). При этом вычисления удобнее вести от точки D, поскольку она остается неподвижной (δ _D=0)и эту точку можно принять за начало координат.

Δ_С = Δ l₃ = = = – 1,25ž 10^-4м ≈ – 0,13мм (вверх);

δ_В = δ_С +Δ l₂ = – 0,13ž10^-3 + = – 0,13ž10^-3 + =

= – 0,13ž10^-3 + 2,5ž10^-4 = 0,12ž10^-3м = 0,12мм (вниз);

δ_A= δ_В +Δ l₁= 0,12ž10^-3 + = 0,12ž10^-3 + =

= 0,12ž10^-3 + 4,17ž10^-4 = 0,54ž10^-3м = 0,54мм (вниз)

Из эпюры перемещений (рис.1ж) видно, что некоторое сечение (точка К) не перемещается. Сечения, расположенные выше точки К, перемещаются вверх (сжатие); сечения, расположенные ниже точки К, перемещаются вниз (растяжение).

Полное удлинение стержня составляет величину Δ l = 0,54мм

 

Вопросы для самопроверки

1. Как строится диаграмма растяжения?

2. Дать определение продольной силы.

3. Как определить знак продольной силы N?

4. Что называется пределом прочности?

5. Что называется пределом пропорциональности?

6. Что называется пределом текучести?

7. Что называется пределом упругости?

8. Как формулируется закон Гука при растяжении?

9. Что показывает модуль упругости 1-го рода при растяжении (сжатии)?

10. Что такое коэффициент Пуассона?

11. Как строятся эпюры продольных сил и деформаций?

12. От каких факторов зависит величина запаса прочности и чем она характеризуется?

13. В чём заключается сущность метода сечений?

14. Что представляет собой эпюра продольных сил?

15. По какой формуле вычисляются нормальные напряжения в сечениях балки?

16. Как определить абсолютное удлинение стержня?

 

 

Тема 3. Сдвиг и кручение

 

Кручение — один из видов деформации тела. Возникает в том случае, если нагрузка прикладывается к телу в виде пары сил в его поперечной плоскости. При этом в поперечных сечениях тела возникает только один внутренний силовой фактор — крутящий момент М_кр. Примеры кручения: пружины растяжения-сжатия, валы.

Угол Δφ закручивания цилиндрического стержня в границах упругих деформаций под действием момента М_кр может быть определён из уравнения закона Гука для случая кручения:

{\displaystyle \varphi _{}={T\ell \over J_{0}G},} Δφ = , (3.1){\displaystyle \varphi _{}={T\ell \over J_{0}G},}{\displaystyle \varphi _{}={T\ell \over J_{0}G},}

где: {\displaystyle J_{0}}I_p = – полярный момент инерции; d {\displaystyle \ell } ‒ диаметр стержня; l – длина стержня; G – модуль сдвига (модуль упругости II-го рода).

Отношение угла закручивания Δφ к длине {\displaystyle \ell }l называют относительным углом закручивания Θ:

Θ = (3.2){\displaystyle \theta ={\frac {\varphi }{\ell }}}

Деформация кручения является частным случаем деформации сдвига.

Касательные напряжения {\displaystyle \tau _{r}}τ, возникающие в условиях кручения, определяются по формуле:

τ = {\displaystyle \tau _{r}={T\cdot r \over J_{0· ρ, (3.3)

где ρ – расстояние от оси кручения.

Очевидно, что касательные напряжения достигают наибольшего значения на поверхности вала при {\displaystyle r_{max}=R} ρ = d/2 и при максимальном крутящем моменте {\displaystyle T_{max}} . Это даёт возможность записать условие прочности при кручении в таком виде:

τ = ≤ [ τ ], (3.4) {\displaystyle \tau _{max}={T_{max}\cdot R \over J_{0}}={\frac {T_{max}}{W_{p}}}}

где W_p = — полярный момент сопротивления; [ τ ] ‒ допускаемые касательные напряжения.{\displaystyle \tau _{max}={\frac {T_{max}}{W_{p}}}\leq [\tau ]}

Условие жесткости при кручении выглядит так:

(3.5)

где [ Ө ] – допускаемый относительный угол закручивания.

Используя эти условия, можно или по известным силовым факторам, которые создают крутящий момент , найти полярный момент сопротивления I_p и далее, в зависимости от той или иной формы, найти размеры сечения, или наоборот — зная размеры сечения, можно вычислить наибольшую величину крутящего момента, которую можно допустить в сечении, которое в свою очередь, позволит найти допустимые величины внешних нагрузок.

При изучении деформации от сдвига необходимо обратить внимание на полную аналогию между формулами закона Гука при растяжении (сжатии) и при сдвиге, а также понять, что явление сдвига нельзя рассматривать отдельно от растяжения (сжатия).

В случае кручения в поперечных сечениях возникают только касательные напряжения, которые распределяются по сечению неравномерно, изменяясь по линейному закону от ”0” в центре сечения до максимального значения на наружном контуре сечения.

Касательные напряжения в двух взаимно перпендикулярных сечениях равны по величине и противоположны по знаку. Это свойство касательных напряжений называют законом парности касательных напряжений.

 

При выполнении расчетов на кручение следует понять основные правила построения эпюр крутящих моментов, используя метод сечений, а также построение эпюр углов закручивания.