Вопросы.
1. Гипотеза де Бройля. Опыты Дэвиссона и Джермера. Дифракция микрочастиц. Принцип неопределенности Гейзенберга.
Французский ученый Луи де Бройль, выдвинул гипотезу об универсальности корпускулярно-волнового дуализма. Согласно де Бройлю, с каждым микрообъектом связываются, с одной стороны, корпускулярные характеристики – энергия Е и импульс р, а с другой – волновые характеристики – частота n и длина волны l. Количественные соотношения, связывающие корпускулярные и волновые свойства частиц, такие же, как для фотонов:
.
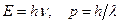В. Гейзенберг,пришел к выводу, что объект микромира невозможно одновременно с любой наперед заданной точностью характеризовать и координатой и импульсом. Согласно соотношению неопределенностей Гейзенберга, микрочастица (микрообъект) не может иметь одновременно и определенную координату (x, y, z), и определенную соответствующую проекцию импульса (px, py, pz), причем неопределенности этих величин удовлетворяют условиям
, 
, 
, (4)
2. Волновая функция, ее статистический смысл и условия, которым она должна
удовлетворять.
волны де Бройля (микрочастицы) не обладают всеми свойствами электромагнитных волн. Например, электромагнитные волны представляют собой распространяющееся в пространстве электромагнитное поле. Распространение волн де Бройля не связано с распространением в пространстве какого-либо электромагнитного поля.
Единственное правильное толкование волн материи, позволяющее согласовать между собой описанные факты, это статистическое толкование: интенсивность волны пропорциональна вероятности обнаружить частицу в данном месте. Для того, чтобы описать распределение вероятности нахождения частицы в данный момент времени в некоторой точке пространства, вводят функцию 
, называемую волновой функцией (или псифункцией). Определяли ее так, чтобы вероятность d W того, что частица находится в элементе объема d V, равнялась произведению 
и элемента объема d V:
. (6)
Физический смысл имеет не сама функция Y, а квадрат ее модуля: 
, где Y* – функция, комплексно сопряженная с Y. Величина имеет смысл плотности вероятности: 
, т.е. определяет вероятность нахождения частицы в единичном объеме в окрестности точки с координатами x, y, z. Так как пребывание частицы где-либо в пространстве есть достоверное событие и его вероятность должна быть равна единице, то это значит, что волновая функция удовлетворяет условию нормировки вероятностей:
.
3.Уравнение Шредингера. Движение свободной частицы.
Уравнение Шредингера, как и все основные уравнения физики (например, уравнения Ньютона в классической механике и уравнения Максвелла для электромагнитного поля), не выводится, а постулируется. Правильность этого уравнения подтверждается согласием с опытом получаемых с его помощью результатов, что, в свою очередь, придает ему характер закона природы. Уравнение Шредингера имеет вид:
, (8)
где 
, m – масса частицы, D – оператор Лапласа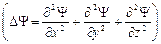 
, i – мнимая единица, 
– функция потенциальной энергии частицы в силовом поле, в котором она движется, – искомая волновая функция частицы.
Свободной называется частица, движущаяся в отсутствие внешних силовых по- лей. Рассмотрим одномерный случай движения частицы вдоль оси Ox. Силы на ча- стицу не действуют, т. е. потенциальная энергия U (x) = const и ее можно принять равной нулю. Тогда полная энергия частицы (в нерелятивистском случае) совпадает кинетической энергией. В этом случае уравнение Шредингера имеет вид:
∂2 ψ
∂ x 2 +
Частным решением уравнения (7) является функция ψ(x) = A exp(jkx), где
A = const и k = const. Собственные значения энергии:
E = ħ 2 k 2/(2 m )
2 m E ψ=0. (7)
ℏ2
4.Частица в одномерной потенциальной яме. Прохождение частицы сквозь потенциальный барьер.
Квантовая частица в потенциальной яме.
Рассмотрим движение частицы вдоль оси Ox в одномерной прямоугольной по- тенциальной яме, имеющей две различные конфигурации: 1) обе стенки бесконечно высокие; 2) одна из стенок имеет бесконечную высоту, а вторая – конечную. Также
рассмотрим частицу в параболической потенциаль- ной яме (гармонический осциллятор).
Конфигурация 1. Ширина ямы равна ℓ. Потен- циальная энергия равна нулю в интервале x = (0, ℓ) и обращается в бесконечность при x = 0 и x = ℓ (см. рис.1, а). Уравнение Шредингера для данного случая имеет вид:
Рисунок 1 – Потенциальная яма с
∂2 ψ 2
∂ x 2+ k
где
ψ=0, (10)
бесконечно высокими стенкам (а) и собственные значения энергии частицы в яме (б)
k 2 = 2 mE / ħ 2. (10а)
Общее решение уравнения (10) имеет вид:
ψ(x)= A sin(kx +α), (11) где A и α – произвольные постоянные.
Волновая функция должна удовлетворять стандартным условиям. Из (11) видно, что ψ(x) однозначна и конечна. Она должна быть еще непрерывной: вне ямы частица быть не может, т. е. вне ямы ψ(x) = 0, и для непрерывности пси-функции необходимо равенство ее нулю на границах ямы, т. е. ψ(0) = 0 и ψ(ℓ) = 0. Из условия ψ(0) = 0 сле- дует A sin(α) = 0 и α = 0. Из условия ψ(ℓ) = 0 имеем:
A sin(kℓ) = 0, kℓ = π n, где n – целое число, не равное нулю (при n = 0 имеем ψ = 0, т. е. частицы вообще нет).
Выразив отсюда k и подставив в (10а), получим:
π2ℏ2 2
En = 2 m ℓ 2 n
Энергия оказалась квантованной и ее спектр – дискретный
.