Кристаллическая решётка вещества – это упорядоченное расположение частиц (атомов, молекул, ионов) в строго определённых точках пространства. Точки размещения частиц называют узлами кристаллической решётки.
В зависимости от типа частиц, расположенных в узлах кристаллической решётки, и характера связи между ними различают 4 типа кристаллических решёток: ионные, атомные, молекулярные, металлические.
Атомными называют кристаллические решётки, в узлах которых находятся отдельные атомы, которые соединены очень прочными ковалентными связями. В природе встречается немного веществ с атомной кристаллической решёткой. К ним относятся бор, кремний, германий, кварц, алмаз. Вещества с атомной кристаллической решёткой имеют высокую температуру плавления, обладают повышенной твёрдостью.
Кристаллическая решётка характеризуется периодической повторяемостью структуры. Благодаря такой периодичности для описания кристаллической структуры достаточно знать размещение атомов в элементарной ячейке. Структура кристалла образуется путём параллельных дискретных переносов (трансляций) этой ячейки. В соответствии с симметрией кристалла его элементарная ячейка может иметь разные формы: куба, косоугольного или прямоугольного параллелепипеда, треугольной, четырехугольной или шестиугольной призмы. Наличием у кристаллов такой кристаллической решётки объясняются анизотропия кристаллов, плоская форма их граней, постоянство углов и другие законы кристаллографии. Кристаллическая структура не является статической конструкцией. Образующие её атомы или молекулы колеблются около определённых положений равновесия. С повышением температуры колебания частиц усиливаются, что приводит к разрушению кристаллической решётки и к переходу вещества из кристаллического состояния в жидкое.
В чистом виде кре́мний был выделен в 1811 году французскими учеными Жозефом Луи Гей-Люссаком и Луи Жаком Тенаром. Кристаллическая решетка кремния – кубическая гранецентрированная, типа алмаза, параметр решётки (а) равен 0,54307 нм (при высоких давлениях получены и другие полиморфные модификации кремния), но из-за большей длины связи между атомами кремния по сравнению с длиной связи между атомами углерода, твёрдость кремния значительно меньше, чем алмаза. Кремний хрупок, только при нагревании выше 800 °C он становится пластичным веществом. Интересно, что кремний прозрачен к инфракрасному излучению, начиная с длины волны 1.1 мкм.
Содержание кремния в земной коре составляет по разным данным от 27,6 до 29,5 %. Таким образом, по распространённости в земной коре кремний занимает второе место после кислорода.
Монокремний характеризуется наличием тетраэдрических ковалентных связей: у каждого атома имеется четыре ближайших соседа, находящихся на равном расстоянии, причём угол между направлениями на любые два из них равен 120O. Таким образом, каждый атом находится в центре правильного тетраэдра, четыре вершины которого связаны с этим атомом ковалентными связями.
Следует особо оговорить, какие именно частицы принадлежат ячейке, чтобы не учитывать одни и те же по нескольку раз, так как каждая грань является общей для двух параллелепипедов, ребро – для четырех, а вершина – для восьми.
На словах структуру алмаза можно описать так. Это гранецентрированная кубическая решетка с четырьмя дополнительными частицами (рис. 1).
Рис. 1. Кристаллическая структура кремния
Их положение определим следующим образом. Разобьем кубическую ячейку на восемь маленьких структур, путём деления её тремя плоскостями, параллельными граням и проходящими через центр ячейки. Из полученных восьми кубиков выберем четыре не имеющие общей грани, переходящие один в другой при отражении относительно рёбер кубиков. В центр объема каждого из этих четырёх «восьмушек» поместим по частице. Иначе эту решётку можно представить как две гранецентрированные решетки, смещенные одна относительно другой на четверть главной диагонали куба.
Итак, кристаллическая решетка кремния состоит из тетраэдров (рис. 1); расстояние между смежными атомами около 0,25 нм. Ребро элементарной ячейки это постоянная решетки a, равная 0,54307 нм.
ИНДЕКСЫМИЛЛЕРА
Сопротивление тензорезистора (ТР), сформированного в кремнии, зависит не только от механического напряжёния и от напряжённости электрического поля но и от ориентации ТР относительнокристаллографических осей. Оценивать направление, т. е. «ориентироваться» в кристаллической решётке, принято с помощью кристаллографических осей.
Кристаллографические оси это направления, определяемые рёбрами элементарной ячейки. Для кубической системы типа алмаза эти оси взаимно перпендикулярны.
Для определения чувствительности преобразователя необходимо определить способ задания и задать оптимальную плоскость среза кристалла а также направление оси чувствительности ТР в выбранной плоскости.
В кристаллографии за координатные оси принимают только направления рёбер кристалла. Начало координат в пространстве кристалла выбирают в одном из его узлов.
Числовые параметры грани (параметры Вейсса). Если какая-либо грань кристалла отсекает от всех трёх координатных осей целое число осевых единиц (в качестве осевых единиц принимаются постоянные решётки), то в решётке найдётся бесконечное множество параллельных этой грани сеток, отсекающих от осей кратное число осевых единиц. Это есть простое следствие решётчатого строения кристаллов.
Если кристалл соотносится к трём координатным осям X, Y, Z, то первый индекс всегда относится к оси X, второй – к оси Y, третий – к оси Z.
На рис. 2 грань ABC отсекает от осей X, Y, Z соответственно 2, 4, 2 осевых единиц. Передвигая грань параллельно ей самой к началу координат, всегда можно придать ей такое положение, при котором она отсечёт от осей наименьшие числа осевых единиц. В нашем примере это случится тогда, когда грань займёт положение A 1 B 1 C 1; отсекаемые ею числа осевых единиц равны 1, 2, 1 и не имеют общего делителя. Этими числовыми параметрами данной грани, вполне определяется ориентировка всей серии параллельных плоских сеток.
Рис.2.Числовые параметры граней A 1 B 1 C 1 и ABC равны 1,2,1 и 2,4,2.
Индексы этих граней равны 2,1,2
Если грань пересекает только две оси (рис. 3), то числовой параметр по третьей оси будет равен бесконечности.
Рис.3. Числовые параметры грани, пересекающей оси X и Y и параллельной оси Z, равны 1,2,∞. Индексы этой грани равны 2,1,0
Грань, изображённая на рис.3, имеет числовые параметры 1, 2, ∞. Наконец, если грань пересекает только одну ось, то числовой параметр по этой оси равен единице, а числовые параметры по двум другим осям равны ∞. На рис. 4 изображена грань с числовыми параметрами ∞, 1, ∞.
Рис. 4. Числовые параметры грани равны ∞,1,∞. Индексы грани равны 0,1,0
Индексы Миллера – это тоже кристаллографические индексы, целые числа, характеризующие расположение граней в кристалле.
1. Индексы грани кристалла. Обычно для обозначения граней или нормалей к граням применяют не числовые параметрыВейсса, а обратные им значения, приведенные к целым числам и называемые индексами Миллера. Если числовые параметры равны m, n, p, то индексы Миллера h, k, l получаются из соотношения:
причём из полученного соотношения 
выбирается отношение наименьших целых чисел.
Например, из числовых последовательностей 1, 2, 3 получаем соотношение
т. е. индексы 6, 3, 2. Из числовых параметров 1, 2, ∞ получаем индексы 2, 1, 0.
Для обозначения одной грани применяют символ грани, состоящий из трёх индексов, поставленных в круглые скобки. Для приведенных примеров соответствующие символ грани будут иметь вид: (632) и (210).
Если плоскость параллельна одной из осей, то точка пересечения с этой осью принимается за бесконечность, а соответствующий индекс — за ноль. Если плоскость пересекает ось в области отрицательных значений, то соответствующий индекс будет отрицательным. Для указания этого над индексом помещается знак «минус»: (h, 
, l). Символ (0 
1) означает грань, параллельную оси X, пересекающую ось Y в отрицательной части и пересекающую ось Z с положительной стороны; числовые параметры этой грани равны: ∞, 
Символ{ h, k, l } означает все грани, в том числе и грань (h, k, l).
В качестве примера на рис. 5 приведены индексы Миллера некоторых наиболее важных плоскостей кубического кристалла.
Рис.5. Индексы Миллера некоторых плоскостей её кубической решетки
Во многих случаях различающиеся индексами Миллера плоскости эквивалентны между собой как в кристаллографическом, так и в физическом смысле. Например, кристаллографическая эквивалентность плоскостей, служащих гранями куба: «(100), (010), (001), (
), (
), (
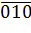)», проявляется в том, что они совмещаются друг с другом при повороте вокруг соответствующих осей на угол, кратный 90°.
Физическая эквивалентность состоит в том, что все они характеризуются одинаковой структурой в расположении узлов решетки и поэтому обладают одинаковыми физическими свойствами. Семейство эквивалентных плоскостей обозначается фигурными скобками, например {100}.
Каждой кристаллографической плоскости свойственна своя плотность атомов на единицу площади. У кремния плоскость (111) является плоскостью спайности; по ней, как правило, распространяются трещины и происходит раскалывание кристалла.
Для разных кристаллографических плоскостей оказываются разными свойства и параметры кристалла: оптические свойства, скорость травления и др. Поэтому пластины для изготовления интегральных датчиков шлифуют точно по заранее заданной кристаллографической плоскости, используя для контроля дифракцию рентгеновских лучей.
2. Индексы узла кристалла. Положение любого узла решетки определяется заданием трёх координат. Следует иметь в виду, что отрезки на кристаллографических осях по трём направлениям измеряются не в одинаковом масштабе, а соответствующими периодами трансляции a, b, c. Если за единицы измерения длин принять параметры решетки, то координатами узла будут просто числа m, n, р. Их называют индексами узла и записывают следующим образом [[ m n р ]].
3. Индексы рёбра кристалла или какого-либо направления в нём. Если начало координат, как всегда, выбрано в узле решетки и если возможное ребро кристалла проходит через начало координат, то для определения направления ребра достаточно знать координаты ближайшего к началу координат узла, находящегося на ребре. Так как осевые единицы, считаются известным для каждого данного вещества, то для обозначения ребра берут только числовые множители осевых единиц. Эти числа называются индексами ребра; поставленные в квадратные скобки, они образуют символ ребра [123].
Направления, проходящие параллельно оси X, получают символ [100], направления, параллельные оси Y, - символ [010], параллельные оси Z, - символ [001]. Противоположные направления обозначаются отрицательным знаком над символом.
Семейство эквивалентных направлений принято обозначать ломаными скобками, например 