Пусть на жестко закрепленную по контуру мембрану радиусом а и толщиной h действует давление q. Тензорезистор расположен на расстоянии r от центра мембраны на её обратной, по отношению к приложенному избыточному давлению, стороне. Радиальное σr и тангенциальное σt напряжения в этой точке можно рассчитать по формулам:
где ν – коэффициент Пуассона.
Если материал мембраны изотропен, то радиальное и тангенциальное напряжения на поверхности мембраны не зависят от угла θ. В этом случае напряжения определяются только расстоянием r от центра мембраны, как показано на приведенном рисунке (рис. 37). Линейная зависимость между приложенным давлением q и механическим напряжением справедлива лишь для малых прогибов мембраны (меньших её толщины h), при которых, как предполагается, отсутствуют напряжения в нейтральной плоскости мембраны. На рисунке показано распределение механических напряжений в тензорезисторе, расположенном на круглой мембране.
Рис. 37 Напряжения 
и 
в круглой мембране
Учет анизотропии механических свойств кремниевых упругих элементов теоретически может быть произведен с различной степенью приближения к эксперименту. Однако возрастающая при этом сложность решения иногда может оказаться неоправданной. В ряде случаев учёт анизотропии приведет к такому отличию от изотропного случая, которое практически проверить весьма сложно из-за значительного технологического разброса характеристик интегральных преобразователей. Тем не менее, строгие решения, описывающие распределения механических напряжений в анизотропных кремниевых упругих элементах различной формы, представляют не только теоретический, но и важный практический интерес.
|
|
В общем случае, при учете анизотропии упругих свойств кремния радиальное σr (r, θ) и тангенциальное σt (r, θ) напряжения будут являться функциями не только радиуса но и угла на мембране. Компоненты тензора механических напряжений в системе координат, связанной с ТР, можно выразить через радиальное и тангенциальное напряжения следующим образом:
где 
угол поворота продольной оси тензорезистора относительно радиус-вектора в точку расположения ТР. Как видно из рисунка:
Таким образом, в системе координат, связанной с плоскостью упругого элемента, угол 
характеризует анизотропию упругих свойств кремния, а угол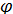 
– анизотропию тензорезистивных свойств через анизотропию тензорезистивных коэффициентов.
В практических разработках ИТП чаще всего встречаются радиально-тангенциальное расположение ТР. В этом случае для радиальных ТР-
φ = 0;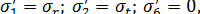 
а для тангенциальных-
φ = 0+90°; 
Сделаем допущение: длина тензорезистора много меньше радиуса мембраны.
Как видно из приведенного рисунка, наиболее интересными точками расположения тензорезистора является центр мембраны и её периферия. Поэтому будем рассматривать, в первую очередь, чувствительность ТР, расположенных в этих зонах. Как показывает анализ, во всех случаях тнзорезисторы можно расположить так, что они будут иметь противоположные знаки приращения сопротивления. Это позволяет создавать на одной мембране полную мостовую схему, в каждом плече которой включён ТР, изменение которого соответствует увеличению чувствительности всего преобразователя. Кроме того, на одной мембране можно разместить несколько мостовых схем для резервирования.
|
|
ПРИЛОЖЕНИЕ 2