Абсолютная и относительная погрешности.
Интерполирование функций.
В большинстве случаев при измерениях, вычислениях, при выполнении операций над действительными числами получают не точные, а приближённые значения величин.
Модуль разности между точным числом х и его приближённым значением a называется абсолютной погрешностью приближённого значения:  .
.
Число а называется приближённым значением точного числа х с точностью до 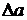 , если абсолютная погрешность приближённого значения а не превышает
, если абсолютная погрешность приближённого значения а не превышает 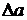 , т.е.
, т.е. 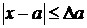 .
.
Относительной погрешностью  приближённого значения а числа х называется отношение абсолютной погрешности
приближённого значения а числа х называется отношение абсолютной погрешности 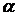 этого приближения к числу а:
этого приближения к числу а: 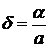 .
.
Задача приближения функций состоит в представлении известных или неизвестных функций с помощью других, более простых функций.
Интерполирование является одним из способов приближения функций и применяется в тех случаях, когда функция задаётся таблицей своих значений в некоторых точках.
Интерполяция функции 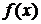 , заданной в точках
, заданной в точках 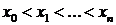 (узлы интерполирования) отрезка
(узлы интерполирования) отрезка 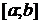 , – подбор функции
, – подбор функции 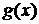 , значения которой в узлах интерполирования совпадают с
, значения которой в узлах интерполирования совпадают с 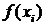 ,
,  . Другими словами, интерполяция – это восстановление функции
. Другими словами, интерполяция – это восстановление функции 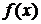 на отрезке
на отрезке 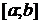 по известным значениям этой функции в точках
по известным значениям этой функции в точках 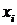 ,
,  .
.
Функцию 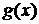 часто ищут в виде многочлена n -ой степени (степень многочлена на 1 меньше количества узлов интерполирования).
часто ищут в виде многочлена n -ой степени (степень многочлена на 1 меньше количества узлов интерполирования).
Интерполяционный многочлен Лагранжа.
Если для n+1 различных значений аргумента 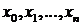 известны соответствующие значения
известны соответствующие значения 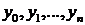 некоторой функции
некоторой функции 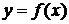 , где
, где 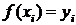 (
( ), то для этой функции можно записать интерполяционный многочлен Лагранжа:
), то для этой функции можно записать интерполяционный многочлен Лагранжа:
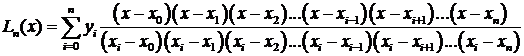 .
.
Пример 1. Функция задана таблицей:
| х | -1 | |||
| f(x) | -11 | -3 |
Составить интерполяционный многочлен Лагранжа и вычислить значение функции в точке х=0.
----------------------------------------------------------------------------------------------------------------
Абсолютная и относительная погрешности. Интерполирование функций. Стр. 1
Решение. 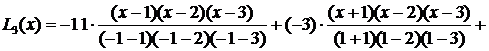
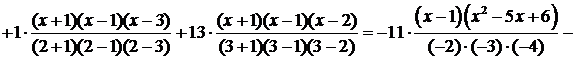
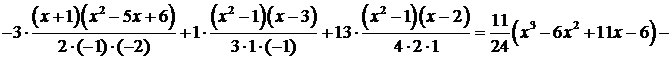
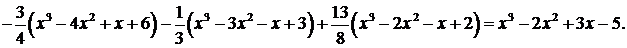
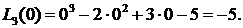
Метод наименьших квадратов.
При решении задач в различных областях естествознания приходится пользоваться эмпирическими формулами, составленными на основе результатов опыта и наблюдения. Способ наименьших квадратов – один из лучших методов получения таких формул.
Пусть необходимо установить функциональную зависимость между двумя величинами х и у. При этом произведено n измерений этих величин. Результаты измерений занесены в таблицу:
| x | 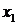
| 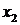
| … | 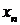
|
| y | 
| 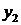
| … | 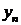
|
Можно предположить, что между этими величинами существует линейная зависимость
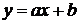 ,
,
где a и b – некоторые параметры, которые определяются из системы:
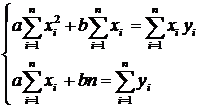 .
.
Пример 2. Объём реализации некоторых товаров за истёкший период представлен в таблице:
| Годы | |||||||||
| Объём, млн.руб. |
Составить линейную эмпирическую формулу и сделать прогноз на 2013 год.
Решение. Т.к. годы идут по порядку, то можно заменить их порядковыми номерами:
| x | ||||||||||
| y | ||||||||||
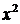
| ||||||||||
| xy | ||||||||||
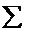
|
----------------------------------------------------------------------------------------------------------------
Абсолютная и относительная погрешности. Интерполирование функций. Стр. 2
Составим систему для определения параметров a и b:
 .
.
Решив систему, получим 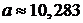 ,
, 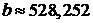 .
.
Тогда линейная эмпирическая формулу имеет вид:
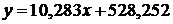 .
.
Вычислим прогнозируемое на 2013 год значение:
 .
.
Задачи для самостоятельного решения.
№1. Найти интерполяционный многочлен Лагранжа для функции, заданной таблицей:
| х | -1 | ||||
| f(x) |
№2. Составить линейную эмпирическую формулу:
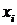
| 1,5 | 2,5 | 3,5 | |||
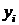
| 0,12 | 1,26 | 2,32 | 3,25 | 4,35 | 5,52 |
----------------------------------------------------------------------------------------------------------------
Абсолютная и относительная погрешности. Интерполирование функций. Стр. 3