Задания для письменной части экзамена по курсу
«Аналитическая геометрия и линейная алгебра»
На факультете радиофизики и компьютерных технологий
Курс, 1 семестр 2018-2019 уч.год.
преподаватель Березкина Л.Л.
1. В параллелепипеде 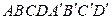 известны векторы
известны векторы 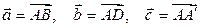 . Найдите сумму
. Найдите сумму 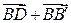 .
.
2. Заданы точки  . Найдите расстояние между ними.
. Найдите расстояние между ними.
3. Заданы точки  . Найдите координаты вектора
. Найдите координаты вектора  и координаты середины отрезка
и координаты середины отрезка  .
.
4. Задана точка  и вектор
и вектор  . Найдите координаты точки
. Найдите координаты точки  .
.
5. Заданы векторы  . Найдите скалярное и векторное произведения векторов
. Найдите скалярное и векторное произведения векторов  и
и  , а также смешанное произведение векторов
, а также смешанное произведение векторов  ,
,  и
и 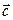 .
.
6. Найдите момент равнодействующей сил  относительно точки
относительно точки  , если эта равнодействующая приложена к точке
, если эта равнодействующая приложена к точке  , а также работу этой равнодействующей при перемещении ее точки приложения из положения
, а также работу этой равнодействующей при перемещении ее точки приложения из положения  в положение
в положение  .
.
7. Задан треугольник  , где
, где  . Найдите длину стороны
. Найдите длину стороны 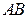 , косинус внутреннего угла
, косинус внутреннего угла  , а также площадь этого треугольника (методами векторной алгебры).
, а также площадь этого треугольника (методами векторной алгебры).
8. Найдите объем треугольной пирамиды 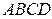 , если
, если 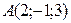 ,
,  ,
,  ,
,  .
.
9. Заданы векторы 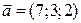 ,
,  ,
,  . Проверьте, являются ли эти векторы компланарными и образуют ли они базис в пространстве. Если векторы некомпланарны, определите ориентацию тройки
. Проверьте, являются ли эти векторы компланарными и образуют ли они базис в пространстве. Если векторы некомпланарны, определите ориентацию тройки  .
.
10. Нарисуйте прямую на плоскости, заданную уравнением  .
.
11. Нарисуйте плоскость, заданную уравнением 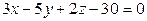 .
.
12. Составьте уравнение прямой на плоскости с угловым коэффициентом, проходящей через точки  .
.
13. Заданы вершины треугольника 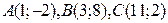 . Составьте:
. Составьте:
а) параметрические уравнения стороны  ;
;
б) канонические уравнения средней линии, параллельной  ;
;
в) общее уравнение высоты, проведенной из вершины  ;
;
г) уравнение медианы, проведенной из вершины  , с угловым коэффициентом.
, с угловым коэффициентом.
14. Даны точки  и прямые
и прямые  Составьте:
Составьте:
а) общее уравнение плоскости, проходящей через точки А, В и С;
б) общее уравнение плоскости, проходящей через точку А и прямую  ;
;
в) общее уравнение плоскости, проходящей через параллельные прямые  и
и  ;
;
г) общее уравнение плоскости, проходящей через прямую  параллельно прямой
параллельно прямой  ;
;
д) общее уравнение плоскости, проходящей через точку С перпендикулярно прямой  .
.
15. Найдите расстояние между параллельными плоскостями  и
и  .
.
16. (3.2.) Составьте уравнение эллипса, фокусы которого лежат на оси абсцисс и симметричны относительно начала координат, если:
2) расстояние между фокусами равно 8 и малая полуось равна 3;
3) большая полуось равна 5 и точка  лежит на эллипсе.
лежит на эллипсе.
17. (3.3.) Составьте уравнение эллипса, фокусы которого лежат на оси ординат и симметричны относительно начала координат, если:
2) расстояние между фокусами равно 12 и большая полуось равна 13;
3) эксцентриситет эллипса равен 0,8, а уравнение одной из директрис  .
.
18. (3.4.) Составьте уравнение гиперболы, если
2) фокусы симметричны относительно начала координат, эксцентриситет равен  , а уравнение одной из директрис
, а уравнение одной из директрис  ;
;
3) гипербола проходит через точку  , а ее вершины находятся в точках
, а ее вершины находятся в точках  и
и 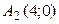 .
.
19. Нарисуйте следующие линии:
 ,
,  ,
,  ,
, 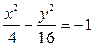 ;
;  ,
,  ,
,  ,
,  ;
;  ,
, 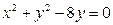 .
.
20. (3.5.) Составьте уравнение гиперболы, фокусы которой лежат на оси ординат и симметричны относительно начала координат, если:
2) расстояние между фокусами равно 10, а эксцентриситет 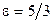 ;
;
3) уравнение одной из асимптот 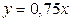 , а действительная полуось равна 6;
, а действительная полуось равна 6;
4) эксцентриситет равен 2,6, а расстояние между директрисами равно  .
.
21. (3.6.) Составьте уравнение параболы, если
1) ее вершина совпадает с началом координат, а фокус находится в точке 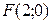 ;
;
2) ветви направлены вверх, а фокальный параметр равен 4;
3) уравнение директрисы  , а фокус находится в точке
, а фокус находится в точке 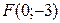 ;
;
4) ее вершина совпадает с началом координат, парабола проходит через точку 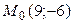 и ось абсцисс является осью параболы.
и ось абсцисс является осью параболы.
22. (3.54.) Определите вид и расположение линии второго порядка:
1)  ; 2)
; 2)  ;
;
3)  ; 4)
; 4) 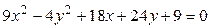 ;
;
5)  ; 6)
; 6)  ;
;
7)  ; 8)
; 8) 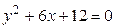 ;
;
9) 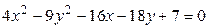 ; 10)
; 10)  ;
;
11) 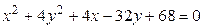 ; 12)
; 12)  .
.
23. (3.56.) Изобразите наплоскости множество точек, координаты которых удовлетворяют уравнениям:
1)  ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4) 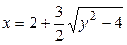 ; 5)
; 5)  ; 6)
; 6)  .
.
24. (3.57.) Изобразите наплоскости множество точек, координаты которых удовлетворяют условиям:
1)  2)
2)  3)
3)  4)
4) 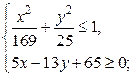
5)  6)
6)  7)
7)  8)
8) 
9)  10)
10) 
25. Нарисуйте следующие поверхности:  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  .
.
26. (4.25.) Определите вид поверхности и нарисуйте эту поверхность, если ее уравнение имеет вид:
1)  ; 2)
; 2)  ; 3)
; 3) 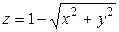 ; 4)
; 4) 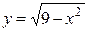 ;
;
5)  ; 6)
; 6)  ; 7)
; 7)  ; 8)
; 8) 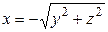 .
.
27. (4.26.) Нарисуйте множество точек пространства, удовлетворяющих системе следующих неравенств:
1)  3)
3)  5)
5) 
2)  4)
4) 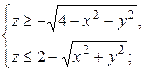 6)
6) 
28. Заданы матрицы  и
и  . Найдите те из произведений
. Найдите те из произведений  ,
,  ,
, 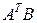 ,
, 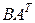 ,
,  ,
,  ,
, 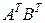 ,
,  , которые существуют.
, которые существуют.
29. Вычислите определители 4-го и 5-го порядков с помощью элементарных преобразований. Например, 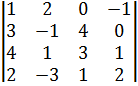 ,
,  .
.
30. Для матрицы третьего порядка вычислите обратную при помощи алгебраических дополнений (например, для матрицы  ).
).
ЗАДАЧИ ДЛЯ УСТНОГО ЭКЗАМЕНА по аналитической геометрии
и линейной алгебре
(числа в экзаменационных задачах будут изменены)
Все задачи решались на практических занятиях, либо предлагались в качестве домашнего задания