Продольные и поперечные колебания балочных элементов
При расчёте динамических нагрузок в случаях старта, разделения ступеней РН, включения и выключения двигательных установок для моделирования силовых корпусов РН наиболее широко используются балочные модели. Поэтому в данном разделе проводится анализ динамического поведения балочных элементов, являющихся базовыми составляющими расчетных моделей для определения нагрузок.
Продольные колебания
Рассмотрим движение (продольное перемещение u (x,t)) выделенного элемента dx (рис.3.1).
| dx |
| f(x,t) |
| N(x) |
| N(x+dx) |
Рисунок 3.1
Относительная деформация 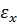 , напряжение
, напряжение  и продольная сила
и продольная сила  определяются следующими соотношениями
определяются следующими соотношениями
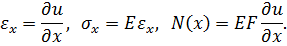
| (3.1.1) |
Здесь E – модуль упругости,
F – площадь поперечного сечения стержня,
произведение  обычно называется продольной жёсткостью балки.
обычно называется продольной жёсткостью балки.
Уравнение продольного движения выделенного элемента запишется так:
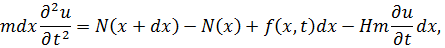
| (3.1.2) |
где m – погонная масса,  – распределённая продольная сила, последний член в (3.1.2) характеризует диссипативные силы.
– распределённая продольная сила, последний член в (3.1.2) характеризует диссипативные силы.
Поделив равенство (3.1.2) на dx и устремив размер выделенного элемента к нулю, получим
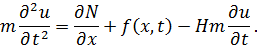
| (3.1.3) |
С учётом соотношения для 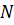 (3.1.1) приходим к уравнению относительно продольного перемещения u (x,t)
(3.1.1) приходим к уравнению относительно продольного перемещения u (x,t)

| (3.1.4) |
Здесь оператор L имеет вид
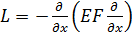 . .
| (3.1.4а) |
Для решения задачи о продольном движении сечений стержня необходимо задать начальные условия в виде поля перемещений и поля скоростей в начальный момент времени.
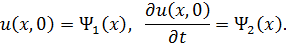
| (3.1.5) |
Кроме того необходимо задать граничные условия на концах стержня. На каждом конце это может быть либо закрепление, либо свободный край.
Закрепление при x =0  , ,
| (3.1.6) |
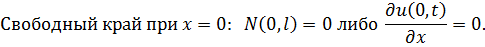
|
Поперечные колебания
Поперечные колебания РН имеют важное значение для анализа нагрузок. Поэтому является важным исследование поперечных колебаний балочных элементов.
Выделим из колеблющейся балки элемент dx и рассмотрим действующие на него силы и моменты.
| Q+dQ |
| M+dM+dQ |
| f (x,t) |
| M |
| Q |
| dx |
Рисунок 3.2
Здесь М – изгибающий момент,
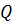 – перерезывающая сила,
– перерезывающая сила,
 – распределённая погонная поперечная сила.
– распределённая погонная поперечная сила.
Уравнение движения в поперечном направлении (уравнение сил)
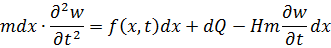
| (3.2.1) |
Здесь 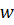 – поперечное перемещение,
– поперечное перемещение,
 – погонная масса,
– погонная масса,
последнее слагаемое характеризует диссипативные силы.
Или

| (3.2.2) |
Уравнение моментов
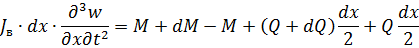
| (3.2.3) |
 – момент инерции вращения единицы длины балки.
– момент инерции вращения единицы длины балки.
Из (3.2.3) следует

| (3.2.4) |
Отсюда, пренебрегая моментом инерции вращения  , будем иметь
, будем иметь
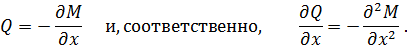
| (3.2.5) |
Воспользуемся соотношением между изгибающим моментом и поперечным перемещением нейтральной линии балки (полученным исходя из гипотезы прямой нормали) (см. Приложение к разделу).
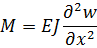
| (3.2.6) |
Здесь 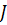 – момент инерции сечения балки.
– момент инерции сечения балки.
Подставляя 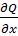 из (3.2.5) в уравнение (3.2.2) с учётом (3.2.6) получим окончательное уравнение поперечных колебаний балки
из (3.2.5) в уравнение (3.2.2) с учётом (3.2.6) получим окончательное уравнение поперечных колебаний балки
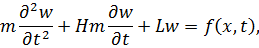
| (3.2.7) |
где

| (3.2.8) |
Отметим, что структура уравнений поперечных колебаний балки (3.2.7) аналогична структуре продольных колебаний стержней:
| инерционный член |
| диссипативный член |
| оператор, характеризующий упругие силы |
| внешние силы |
В силу общности структуры уравнений продольных (3.1.4) и поперечных (3.2.7) колебаний стержней математическая постановка задачи также обладает общностью.
Для решения уравнения (3.2.7) необходимо задать начальные условия – поле поперечных перемещений и скоростей в начальный момент времени

| (3.2.9) |
и граничные условия.
Следует отметить, что число граничных условий на каждом краю (в каждой точке границы) определяется порядком оператора L. В упругих задачах для тонкостенных элементов конструкций (балок, пластин, оболочек) порядок оператора L кратный (2 n). Число граничных условий при этом в каждой точке границы равно n. В случае поперечных колебаний балки порядок оператора L равен четырём, поэтому при решении дифференциальных уравнений на каждом краю требуется выполнение двух граничных условий.
При продольных колебаниях стержней оператор L имеет второй порядок и поэтому на каждом краю задается по одному граничному условию.
На рисунке 3.3 представлены варианты граничных условий при поперечных колебаниях балок, которые должны выполняться при использовании уравнений движения.
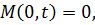 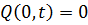
|
w (0, t)=0, 
|
w (0,t)=0, 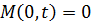
|
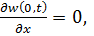 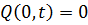
|
| свободный край |
| закреплённый край |
| шарнирный край |
| безинерционный диск, скользящий без трения между двумя жёсткими пластинами из-за наличия вертикальной щели |
| (3.2.10) |
Рисунок 3.3
Четвёртый вариант граничных условий (
 ) математически и физически допустим, но не имеет практического значения.
) математически и физически допустим, но не имеет практического значения.
В дальнейшем будет показано, что при решении задач для упругих систем вариационным путём потребуется выполнение только кинематических (или геометрических) граничных условий, налагаемых на перемещения и углы поворота.
Собственные частоты и формы колебаний
Для решения уравнений колебаний различных типов конструкций, имеющих вид (3.1.4), (3.2.7) наиболее часто используется метод разложения решения по собственным формам колебаний.
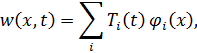 , ,
| (3.3.1) |
где 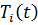 – обобщённые координаты,
– обобщённые координаты,
 – соответствующие формы колебаний.
– соответствующие формы колебаний.
Уравнение для определения собственных частот и форм колебаний получается из уравнений (3.1.4) и (3.2.7) путём отбрасывания диссипативных и внешних сил
 . .
| (3.3.2) |
К уравнению присоединяются соответствующие рассматриваемой задаче однородные граничные условия (3.1.6), (3.2.10).
Решение уравнения (3.3.2) отыскивается в виде
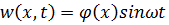 . .
| (3.3.3) |
Тогда уравнение для определения форм колебаний запишется так:

| (3.3.4) |
с соответствующими однородными граничными условиями.
Решением задачи (3.3.4) является совокупность собственных частот wi и отвечающих им собственных форм колебаний 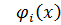 .
.
Отметим также, что амплитуда погонных инерционных сил в соответствии с (3.3.3) будет иметь вид
 . .
| (3.3.4а) |
Неотрицательному симметричному оператору L для континуальной упругой системы соответствует счётное множество собственных частот wi и форм колебаний  . Очевидно, что собственные формы определяются с точностью до константы в виде множителя.
. Очевидно, что собственные формы определяются с точностью до константы в виде множителя.
Симметрия и положительность операторов продольных и поперечных колебаний стержней
Оператор L всех рассматриваемых здесь упругих систем является симметричным и неотрицательным [16]. Свойство симметрии заключается в том, что при любых допустимых функциях u и v справедливо равенство
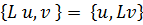
| (3.3.5) |
где скобками {..} обозначено обобщенное скалярное произведение

| (3.3.6) |
Здесь компоненты векторов 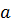 и
и  являются функциями
являются функциями  .
.
К допустимым функциям относятся функции, удовлетворяющие одним и тем же граничным условиям задачи (3.3.2)
Свойство неотрицательности оператора L заключается в том, что
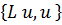 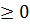
| (3.3.7) |
Покажем, что операторы, описывающие продольные, крутильные и поперечные колебания стержней, удовлетворяют свойствам (3.3.5) и (3.3.7). Для этого подставим оператор L, соответствующий, например, продольным колебаниям (3.1.4а), в формулу (3.3.5) и проинтегрируем дважды по частям в левой части равенства (3.3.5)
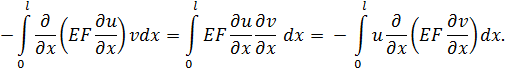
| (3.3.8) |
При интегрировании по частям внеинтегральные члены обращаются в нули, так как функции u и v удовлетворяют однородным граничным условиям.
Из равенства первого и последнего выражений в соответствии (3.3.8) следует симметрия оператора L (3.1.4а).
Равенства первого и второго выражений в соответствии (3.3.8) при  приобретает вид
приобретает вид
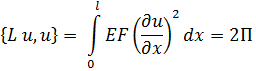
| (3.3.9) |
Из соотношения (3.3.9) видно, что выражение  равно удвоенной потенциальной энергии П при продольных колебаниях стержней и удовлетворяет неравенству (3.3.7). Знак равенства в (3.3.7) имеет место только в том случае, когда
равно удвоенной потенциальной энергии П при продольных колебаниях стержней и удовлетворяет неравенству (3.3.7). Знак равенства в (3.3.7) имеет место только в том случае, когда 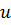 = const, что соответствует смещению стержня как твердого целого при нулевой частоте (w0=0).
= const, что соответствует смещению стержня как твердого целого при нулевой частоте (w0=0).
Покажем, что оператор, описывающий поперечные колебания стержня (3.2.8), также удовлетворяет условию симметрии (3.3.5) и положительности (3.3.7). Подставим оператор (3.2.8) в левую часть формулы (3.3.5) и проинтегрируем дважды по частям

| (3.3.10) |
После четырехкратного интегрирования по частям (двукратного интегрирования правой части (3.3.10)) будем иметь
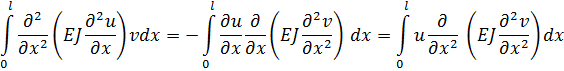
| (3.3.11) |
Все внеинтегральные члены в соотношениях (3.3.10) и (3.3.11) в силу однородных граничных условий (3.2.10) равны нулю (в нуль обязательно обращается первый или второй сомножитель при любых граничных условиях).
Равенство первого и последнего выражения в (3.3.11) указывает на симметрию оператора L.
Из соотношения (3.3.10) при 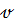 =u получим
=u получим

| (3.3.12) |
где 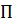 – потенциальная энергия при изгибе стерж – потенциальная энергия при изгибе стерж 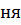
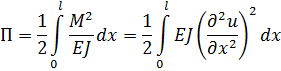
|
Отсюда следует, что при поперечных колебаниях стержней выражение 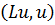 равно удвоенной потенциальной энергии и оператор L является неотрицательным.
равно удвоенной потенциальной энергии и оператор L является неотрицательным.
Равенство нулю выражения 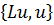 , как и при продольных колебаниях, возможно только при смещении стержня как жесткого целого, т.е. при
, как и при продольных колебаниях, возможно только при смещении стержня как жесткого целого, т.е. при  . В силу равенств (3.3.9) и (3.3.12) выражение
. В силу равенств (3.3.9) и (3.3.12) выражение 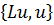 называют энергетическим скалярным произведением. Отметим, что свойствами симметрии, положительности и равенства выражения
называют энергетическим скалярным произведением. Отметим, что свойствами симметрии, положительности и равенства выражения 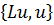 удвоенной потенциальной энергии обладают также операторы теории упругих пластин и оболочек.
удвоенной потенциальной энергии обладают также операторы теории упругих пластин и оболочек.
Положительность собственных частот. Покажем, что собственные частоты симметричного положительного оператора неотрицательны. Обозначим некоторую собственную форму и соответствующую ей собственную частоту через 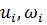 , соответственно. Тогда можно записать тождество
, соответственно. Тогда можно записать тождество
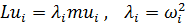 . .
| (3.3.13) |
Умножив обе части (3.3.13) скалярно на  , получим
, получим
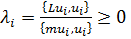 . .
| (3.3.14) |
Последнее равенство следует из неотрицательности оператора 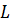 и положительной определённости знаменателя (как приведённой массы).
и положительной определённости знаменателя (как приведённой массы).
Ортогональность собственных форм колебаний. Покажем теперь, что собственные формы 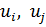 , отвечающие различным собственным числам
, отвечающие различным собственным числам 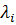 ,
, 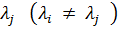 ортогональны.
ортогональны.
Каждая из собственных форм колебаний  и
и 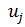 удовлетворяет уравнению (3.3.4):
удовлетворяет уравнению (3.3.4):
 ; ;
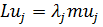 . .
| (3.3.15) |
Умножим скалярно первое равенство на 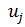 , а второе – на
, а второе – на  и вычтем почленно из первого равенства второе
и вычтем почленно из первого равенства второе
 . .
| (3.3.16) |
В силу симметрии оператора 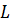 левая часть равенства (3.3.16) равна нулю
левая часть равенства (3.3.16) равна нулю
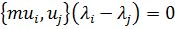 . .
| (3.3.17) |
Из равенства (3.3.17) при различных собственных числах следует ортогональность собственных форм колебаний
 . .
| (3.3.18) |