Продольные колебания
Наиболее просто решается задача о собственных значениях при продольных колебаниях однородного стержня с постоянной погонной массой m и продольной жёсткостью EF.
В этом случае с учётом (3.1.4а) уравнение (3.3.4) примет вид
 , где  .
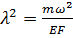| (3.4.1) |
Решение однородного уравнения
 .
| (3.4.2) |
Рассмотрим различные варианты граничных условий
а) края закреплены
| 
|
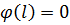
Из первого условия: 
следует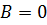 
.
Из второго условия: 
или 
и с учётом (3.4.1)
 
 .
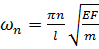
| (3.4.3) |
б) края свободны
| 
|
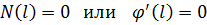
С учётом (3.4.2)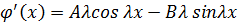 
.
Из первого условия: 
следует 
.
Из второго условия: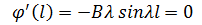 
 .
| (3.4.4) |
Примечание: На рисунках 3.4 и 3.5 показаны продольные перемещения сечений стержня при собственных колебаниях по первым тонам при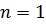 
(формы определяются с точностью до констант в виде множителей).
Кроме того, уравнение (3.4.1) допускает решение в виде константы при нулевой собственной частоте
 
| (3.4.5) |
Этот тон характеризует смещение стержня как твёрдого целого вдоль оси x и называется "тоном твёрдого тела".
Из рассмотренных двух вариантов граничных условий следует любопытный факт: собственные частоты упругих тонов продольных колебаний однородных стержней со свободными и закреплёнными краями совпадают.
в) Приведём для сведения частоты и формы продольных колебаний однородного стержня в случае консольного закрепления.
 , ,
 .
| (3.4.6) |
Поперечные колебания
С учетом постоянных погонной массы m и изгибной жёсткости EJ уравнение для определения собственных частот и форм поперечных колебаний с учётом (3.2.8) и (3.3.4) запишется так:
 , где  .
| (3.4.7) |
Решение уравнения (3.4.7) имеет вид
| (3.4.8) |
Рассмотрим вариант шарнирно опертой балки
| l |
Рисунок 3.6
Граничные условия в опорных сечениях – отсутствие перемещений 
и изгибающих моментов М.
При x= 0
| (3.4.9) |
Или с учётом (3.4.8)
|
отсюда 
.
При x=l
| 
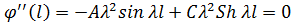
| (3.4.9а) |
Отсюда частотное уравнение (равенство нулю определителя)
| (3.4.9б) |
Тривиальное решение 
=0, 
не представляет интереса. Из равенства (3.4.9б) получаем выражение для приведенной частоты
|
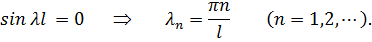
Так как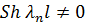 
из равенств (3.4.9а) следует 
.
В итоге с учетом (3.4.7), (3.4.8) будем иметь выражения для собственных частот и форм колебаний шарнирно опертой балки:
 .
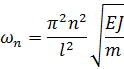
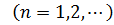| (3.4.10) |
Из приведённых примеров становится ясной схема определения собственных частот и форм колебаний однородных стержней и балок, поэтому далее для сведения приведены частотные уравнения и низшие собственные частоты поперечных колебаний однородных балок с различными граничными условиями.
Поперечные колебания однородной балки с жёстко закреплёнными краями:
| Рисунок 3.7 | Граничные условия: 
|
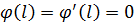
Частотное уравнение:
| (3.4.11) |
Первые две собственные частоты:
 , 
| (3.4.12) |
Поперечные колебания однородной балки со свободными краями:
Рисунок 3.8 | Граничные условия:
равенство нулю изгибающего момента и перерезывающей силы:
|
Частотное уравнение:
|
| (3.4.13) |
Первые две собственные частоты:
| ,
| (3.4.14) |
Здесь повторяется тот же факт, что и для случая продольных колебаний стержней: собственные частоты упругих тонов колебаний однородных балок с жёстко закреплёнными краями и со свободными краями совпадают!
Необходимо отметить, что в случае свободных краев уравнение (3.4.7) допускает два дополнительных решения:
 
 
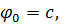
| (3.4.15) |
Эти два решения соответствуют параллельному смещению балки как твёрдого целого 
и повороту балки как твёрдого целого 
. Именуются эти решения "тонами твёрдого тела".
Решения задач о собственных колебаниях более сложных систем осуществляется приближёнными методами, наиболее широко используемым из них является метод конечных элементов.
В случае свободных краев полная система базисных функций, используемая при разложении решения по тонам колебаний, должна учитывать как упругие тона, так и тона твёрдого тела. При этом предварительно тона твёрдого тела ортогонализируются (по Шмидту).
В случае поперечных колебаний балки легко получить ортогональные тона твёрдого тела, соответствующие (3.4.7)
| (3.4.16) |
Здесь 
– координата центра масс балки.
Действительно, с учётом соотношения для центра масс, будем иметь
| (3.4.17) |
Ортогональность тонов твёрдого тела, соответствующих нулевой частоте, и упругих тонов с частотами, отличными от нуля, обеспечивается свойством ортогональности форм колебаний (3.3.18) с различными собственными частотами.
Из свойства ортогональности упругих тонов 
тону твёрдого тела в данном случае для свободной балки следует
| (3.4.18) |
Это означает, что при колебаниях балки со свободными краями на собственных упругих тонах центр её масс, как системы, не смещается (хотя при этом непосредственно координата центра масс балки как твёрдого целого смещается (см. рисунок 3.8 при поперечных колебаниях). Суммарная инерционная сила балки со свободными краями при колебаниях по упругим тонам (3.4.18) как системы равна нулю.
Из свойства ортогональности упругих тонов балки со свободными краями второму тону твердого тела (3.4.16) следует
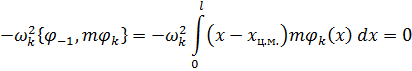
| (3.4.19) |
Из равенства (3.4.19) вытекает следующее.
При колебаниях на упругих тонах балка как система не вращается. Суммарный момент от инерционных сил при колебаниях балки на собственных упругих тонах равен нулю.
Свойства, выраженные равенствами (3.4.18) и (3.4.19), означают "самоуравновешенность" упругих тонов колебаний систем со свободными краями.
В заключение отметим, что любая свободная пространственная конструкция имеет шесть тонов твёрдого тела, соответствующих нулевой собственной частоте. То есть, количество твёрдых тонов соответствует количеству степеней свободы конструкции как твёрдого целого. В общем случае n -кратной собственной частоте соответствует n линейно независимых собственных форм колебаний. Полная система базисных функций при использовании метода разложения по тонам колебаний для свободной конструкции в обязательном порядке формируется из упругих тонов и тонов твёрдого тела. При этом тона твёрдого тела предварительно ортогонализируются по Шмидту.
Приложение к разделу
Формула для изгибающего момента
Приведём для справки вывод часто используемой формулы, связывающей изгибающий момент с прогибом нейтральной линии балки.
| r |
| D j |
| sх <0 |
| + |
| - |
| sх >0 |
| X |
| Z |
| Y |
| D l 1 |
| z |
| нейтральная линия |
| D l 2 |
Рисунок 1.
На рисунке 1 показаны:
– недеформируемый отрезок вдоль нейтральной линии:
|
– отрезок деформированного волокна, удалённого на расстояние z от нейтральной линии с учётом гипотезы прямой нормали:
|
r – радиус кривизны нейтральной линии.
Относительная деформация
| (1) |
Нормальное напряжение в сечении F, перпендикулярном нейтральной линии
| (2) |
Изгибающий момент 
в сечении F, создаваемый нормальными к сечению F напряжениями 
,
| (3) |
или
| (4) |
здесь
| (5) |
– момент инерции сечения F.
Ниже представлено приближённое значение для кривизны нейтральной линии балки 
через прогиб 
с учётом малости квадрата угла поворота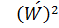 
| (6) |
Окончательно для изгибающего момента с учётом гипотезы прямой нормали приходим к следующей формуле
| (7) |
Подставив в (2) кривизну из соотношения (4), получим связь между нормальными напряжениями в сечении F, перпендикулярном к нейтральной линии, и изгибающим моментом
 .
| (8) |