Задача фильтрации. Базисные фильтры и их идеальные частотные характеристики

Цель работы

Целью работы является изучение реализации и синтеза фильтров в системе MATLAB.

Теоретическая часть

АНАЛОГОВЫЕ ФИЛЬТРЫ

Задача фильтрации. – Понятие фильтра. – Базисные фильтры и их идеальные частотные характеристики. – Задача аппроксимации. – Типовые фильтры нижних частот. – Фильтры Баттерворта и их свойства. – Фильтры Чебышева первого рода и их свойства. – Денормирование и трансформация фильтров.

Задача фильтрации. Базисные фильтры и их идеальные частотные характеристики

Под фильтрацией понимают такое преобразование сигнала, при котором его определенные полезные особенности сохраняются, а нежелательные свойства подавляются. Осуществляется фильтрация при помощи фильтра, представляющего собой динамическую систему с определенными динамическими свойствами.

С помощью фильтрации решают многочисленные задачи, возникающие на практике, в том числе:

1) подавление шумов, маскирующих сигнал;

2) устранение искажения сигнала, вызванного несовершенством канала передачи или погрешностью измерения;

3) разделение двух или более различных сигналов, которые были преднамеренно смешены для того, чтобы в максимальной степени использовать канал;

4) разложение сигналов на частотные составляющие;

5) демодуляция сигналов;

6) преобразование дискретных сигналов в аналоговые;

7) ограничение полосы частот, занимаемой сигналами.

Фильтрацию можно представить, как процесс изменения частотного спектра сигнала в некотором желаемом направлении. Этот процесс может привести к усилению или ослаблению частотных составляющих в некотором диапазоне частот, к подавлению или выделению какой-либо конкретной частотной составляющей и т.п.

Разработка практических методов фильтрации процессов зачастую базируется на следующем принципиальном допущении: спектры полезного сигнала и сигнала помехи не перекрываются. Например, в случае взаимного расположения спектров, показанного на рис. 1, а необходимо потребовать, чтобы фильтр пропускал все частотные составляющие в диапазоне и подавлял частотные составляющие в диапазоне .

Задача фильтрации существенно усложняется, если спектры полезного сигнала и сигнала помехи перекрываются (рис. 1, б). Здесь нельзя однозначно установить границу между полосой пропускания и полосой задерживания. Смещение границы влево приводит к большему искажению полезного сигнала за счет подавления его высокочастотных составляющих, а смещение вправо – к большему искажению за счет помех. В этом случае ставят и решают задачу поиска оптимального фильтра.

Полоса частот, в которой сигналы пропускаются (усиливаются) фильтром, называется полосой пропускания. Полоса частот, где сигналы подавляются (ослабляются) фильтром, называется полосой задерживания. Частоты, лежащие на границе полос пропускания и задерживания, называются граничными частотами.

Рис. 1 Амплитудные спектры полезного сигнала (1) и помехи (2): а – с незначительным перекрытием; б – со значительным перекрытием

В зависимости от взаимного расположения полос пропускания и задерживания различают следующие типы фильтров:

фильтры нижних частот (ФНЧ);

фильтры верхних частот (ФВЧ);

полосовые фильтры (ПФ);

заграждающие (режекторные) фильтры (ЗФ).

Перечисленные выше типы фильтров широко применяются при обработке данных и сигналов. Поэтому их часто называют базисными фильтрами. В идеале базисные фильтры должны иметь амплитудно-частотные характеристики, представленные на рис. 2.

Рис.2. Идеальные АЧХ базисных фильтров

1. Идеальный фильтр низких частот должен пропускать все частотные составляющие в диапазоне и подавлять частотные составляющие в диапазоне (рис. 2, а).

2. Идеальный фильтр высоких частот должен иметь обратные характеристики, то есть пропускать частотные составляющие в диапазоне и поглощать их в диапазоне (рис. 2, б).

3. Полосовой фильтр должен пропускать составляющие с частотами, лежащими в диапазоне и подавлять другие составляющие (рис. 2, в).

4. Заграждающий фильтр должен подавлять составляющие с частотами из диапазона и пропускать другие составляющие без изменения (рис. 2, г).

Покажем, что реализовать фильтры с идеальными характеристиками нельзя. Рас смотрим идеальный ФНЧ, обобщенную частотную характеристику которого можно записать так:

(1)

Частотные характеристики фильтра, построенные по выражению (1), показаны на рис. 3, а. Применив к (1) обратное преобразование Фурье, найдем импульсную переходную функцию идеального ФНЧ

Рис. 3. Характеристики идеального ФНЧ: а – амплитудно-частотная характеристика; б – импульсная переходная функция

Импульсная переходная функция построена на рис. 3, б. Как видно, 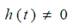при тем самым нарушено условие физической реализуемости системы. Идеальный ФНЧ поэтому реализовать нельзя.