Лекция №3. (2 часа)
Раздел 1. Арифметические и логические основы цифровой техники.
Тема 1.3. Основы булевой алгебры. Схемотехника логических элементов
План
Основные понятия алгебры логики. Логические операции
Законы и теоремы булевой алгебры.
Способы задания логических функций
Цель занятия:
Дидактическая. Изучить основные понятия алгебры логики, законы и тождества, необходимые для преобразования логических выражений, а также различные способы задания логических функций.
Воспитательная. Формирование дисциплины, самостоятельности, логики мышления.
Основные понятия алгебры логики. Логические операции.


Таблица 3.1

Таблица 3.2
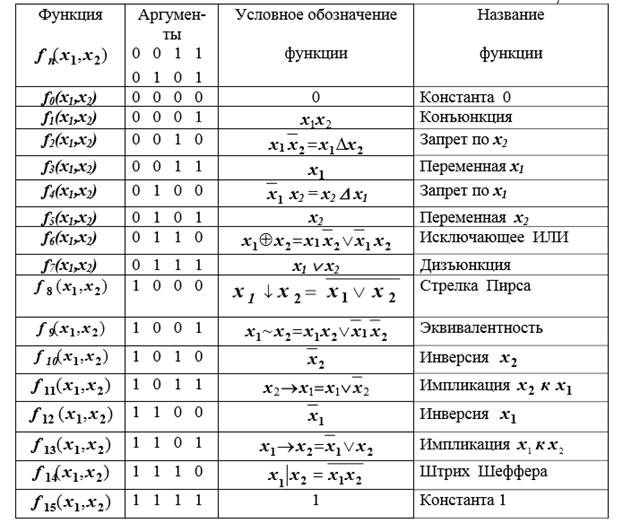

Для булевой функции от одной переменной (n =1) существует четыре различных функции (сингулярные функции) и для их описания потребуется таблица из 4-х строк (табл.3.1) От двух аргументов получим 16 различных булевых функций (бинарные функции). Эти функции представлены в табл. 3.2. Для описания бинарных функций потребуется уже 16 строк и т.д. Поэтому сложные логические функции при большом числе аргуметов обычно представляют как более простые функции от одного или двух аргументов.
Логические операции
Операция дизъюнкции. Это операция логического сложения, иначе операция ИЛИ. Аналитически операция дизъюнкции записывается следующим образом: Y = x1 + x2 = x1 ˅ х2. (3.1)
 ˅
˅
Рисунок 3.1
Выражение (3.1) показывает, Y принимает единичное значение, если хотя бы одна из переменных равна единице. Это выражение можно записать в виде таблицы, которая носит название таблицы истинности (табл.3.3). Эта таблица дает краткую запись следующих действий:
0˅0=0; 0˅1=1; 1˅0=1; 1˅1=1. (3.2)
Условное обозначение элемента, выполняющего операцию дизъюнкции и его схемная реализация, представлены соответственно на рис.3.1, а и б. Кстати, логический элемент в основе работы которого лежит логическая функция ИЛИ называется элемент ИЛИ, а также дизъюнктор. Он может иметь два и более входов, то есть функция ИЛИ может быть реализована на две и более переменных (как правило это 2, 3 и 4).
Таблица 3.3 Таблица 3.4

Операция коньюнкции. Эту операцию также назвают операцией И (операцией логического умножения). Аналитически в случае двух переменных эта операция записывается в виде: Y=x1x2=x1˄x2. (3.3)
Смысл операции коньюнкции заключается в том, что Y=1, если одновременно х1=1 и х2=1, т.е.если для этой операции составить таблицу истинности (табл.3.4), то можно сделать вывод, что содержание таблицы кратко говорит о следующем:
0ˑ0 = 0; 0ˑ1 = 0; 1ˑ0 = 0; 1ˑ1 = 1. (3.4)
В случае n переменных: Y = x1x2x3…хn. (3.5)
Условное графическое обозначение элемента (УГО), выполняющего операцию коньюнкции и его схемная реализация на дискретных элементах представлена соответственно на рис. 3.1, в и г. Элемент, в основе работы которого положена логическая функция ИЮ еще называется коньюнктором.
Операция инверсии. Это операция логического отрицания, иначе операция НЕ. Аналитически это записывается в виде Y = x. Таблица истинности для этой операции показана на рис. 3.1, д. и практически говорит о том, что 1 = 0; 0 = 1. Схемным примером инвертора (а именно так называется логический элемент, реализующий функцию НЕ) может служить ключевой каскад, условное графическое обозначение которого приведено на рис.3.1, е. Кружок на выходе УГО называется индикатором состояния. Он обозначает, что состояние выхода противоположно состоянию входа и говорит в данном случае, что в схеме выполняется операция инверсии.

 (3.6)
(3.6)
Равенства (3.6) отражают принцип двойственности в алгебре логики. Ос-

 (3.7)
(3.7)
Законы и теоремы булевой алгебры

 (3.8)
(3.8)
 (3.9)
(3.9)
Форма (3.8) имеет аналог в обычной алгебре, а форма (3.9) не имеет аналога. Поэтому справедливость равенства (3.9) требует доказательства:[1]

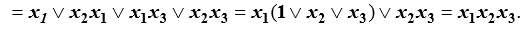 (3.10)
(3.10)

 (3.11);
(3.11); 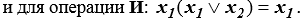 (3.12)
(3.12)
Доказательства равенств (3.11) и (3.12) очень просты:
 (3.13)
(3.13)
Равенство (3.13) соответствует (3.11). Соответственно для операции
 (3.14)
(3.14)
Равенство (3.14) также соответствует (3.11).
Закон склеивания. Как и в предыдущем случае имеется два варианта:
 (3.15)
(3.15)  (3.16).
(3.16).
Доказательство для 3.15:
 (3.17).
(3.17).
При доказательстве 3.16 необходимо раскрыть скобки и воспользоваться правилом 3.7 и законом 3.15:
 (3.18)
(3.18)
Правило де Моргана. Справедливость этого правила вытекает из принципа двойственности булевой алгебры, приведенного в 3.6:
 (3.19)
(3.19)
 (3.20).
(3.20).