№ 13. а) Решите уравнение 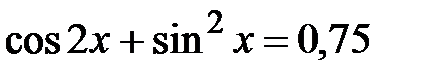 .
.
б) Найдите все корни этого уравнения, принадлежащие отрезку 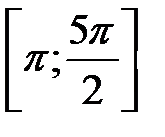 .
.
Решение.
а) 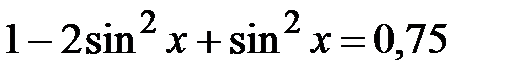 ;
;
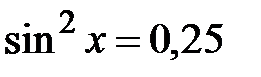 ;
;
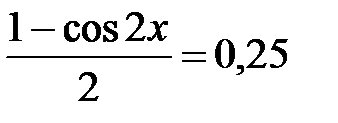 ;
;
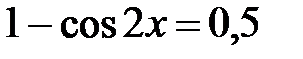 ;
;
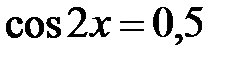 ;
;
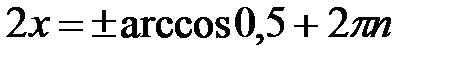 ,
, 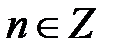 ;
;
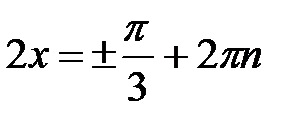 ,
, 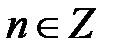 ;
;
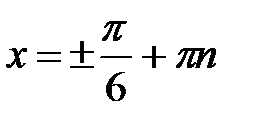 ,
, 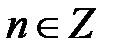 .
.
б) С помощью числовой прямой отберём корни уравнения, принадлежащие отрезку 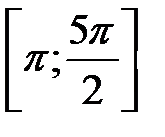 :
:

Если 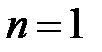 , то
, то 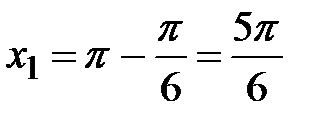 ,
, 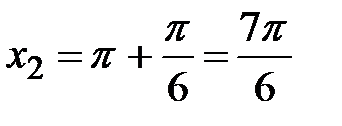 и
и 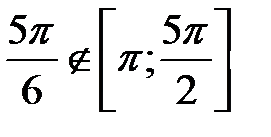 ,
, 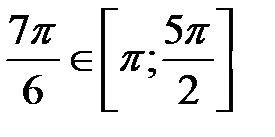 .
.
Если 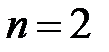 , то
, то 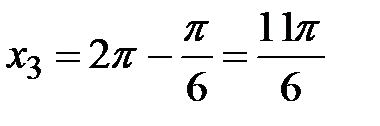 ,
, 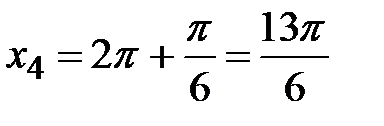 и
и 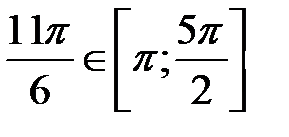 ,
, 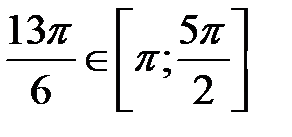 .
.
Если 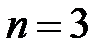 , то
, то 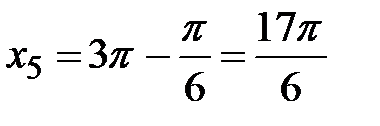 ,
, 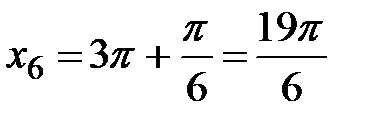 и
и 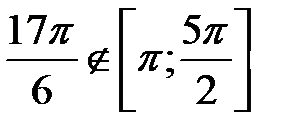 ,
, 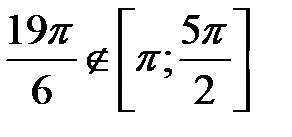 .
.
Получаем корни 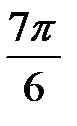 ,
, 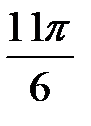 и
и 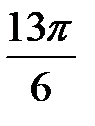 .
.
Ответ: а) 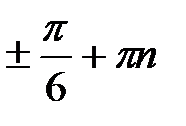 ,
, 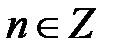 ; б)
; б) 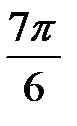 ,
, 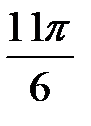 и
и 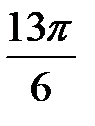 .
.
| Содержание критерия | Баллы |
| Верно получены обоснованные ответы в двух пунктах | |
| Обоснованно получен верный ответ в пункте а) или пункте б), ИЛИ Получен неверный ответ из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения уравнения и отбора корней | |
| Решение не соответствует ни одному из критериев, приведённых выше. | |
| Максимальный балл | 2 |
№ 14. Решите неравенство 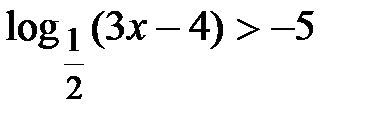 .
.
Решение.
Перепишем данное неравенство в виде
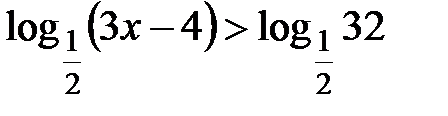 .
.
Так как функция 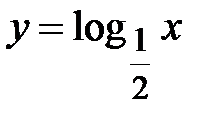 убывающая и определена на множестве положительных чисел, то полученное неравенство равносильно системе:
убывающая и определена на множестве положительных чисел, то полученное неравенство равносильно системе:
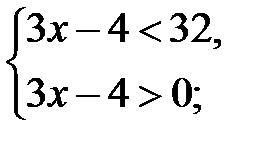
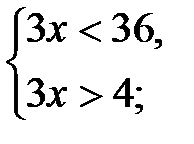
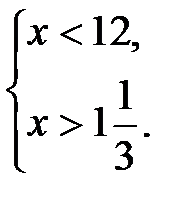
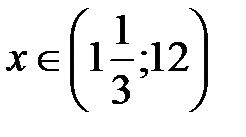 .
.
Ответ: 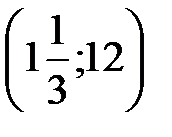 .
.
| Содержание критерия | Баллы |
| Обоснованно получен верный ответ. | |
| При решении учтено убывание функции, но не учтена область определения. ИЛИ Получен неверный ответ из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения. | |
| Решение не соответствует ни одному из критериев, приведённых выше. | |
| Максимальный балл | 2 |
№ 15. Напишите уравнение касательной к графику функции 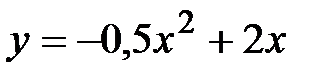 , в точке
, в точке 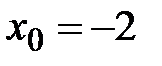 .
.
Решение.
Общий вид уравнения касательной к графику функции 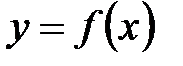 в точке с абсциссой
в точке с абсциссой 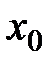 имеет вид
имеет вид 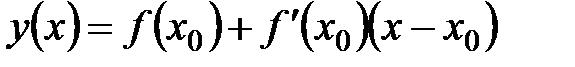 .
.
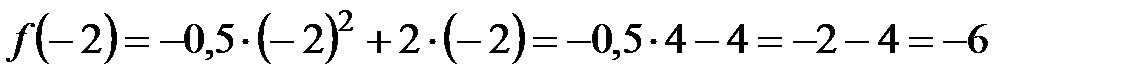 .
.
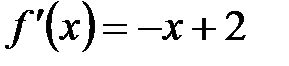 .
.
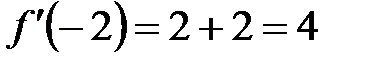 .
.
Тогда 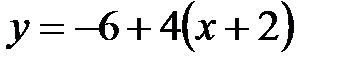 ,
, 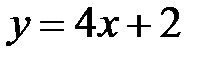 .
.
Ответ: 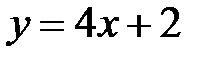 .
.
| Содержание критерия | Баллы |
| Верно получен обоснованный ответ. | |
Допущена ошибка при записи общего вида уравнения касательной к графику функции 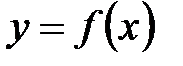 в точке с абсциссой в точке с абсциссой 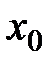 ИЛИ
Допущена ошибка при нахождении производной
ИЛИ
Получен неверный ответ из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения
ИЛИ
Допущена ошибка при нахождении производной
ИЛИ
Получен неверный ответ из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения
| |
| Решение не соответствует ни одному из критериев, приведённых выше. | |
| Максимальный балл | 2 |
№ 16. Трапеция вписана в окружность. Ее основания равны 21 см и 5 см, а один из углов равен 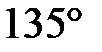 . Найти площадь трапеции.
. Найти площадь трапеции.
Решение.
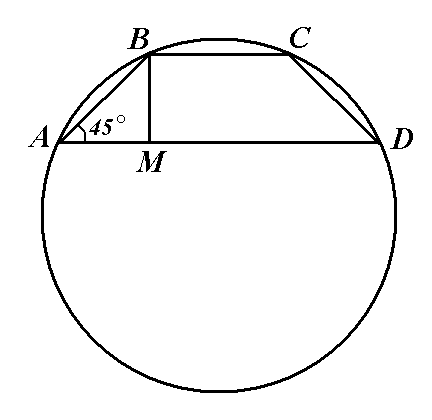 Так как трапеция
Так как трапеция 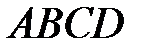 (ВС || AD) вписана в окружность, то она равнобокая: АВ = CD. Проведем высоту ВМ
(ВС || AD) вписана в окружность, то она равнобокая: АВ = CD. Проведем высоту ВМ 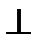 AD, тогда
AD, тогда 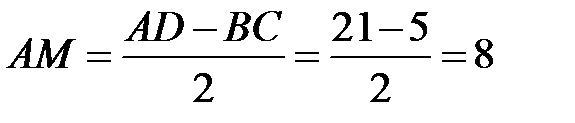 (см).
(см).
Так как 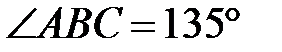 , то
, то 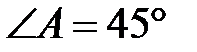 . В
. В 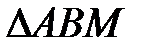
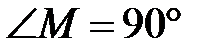 ,
, 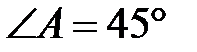 , тогда этот треугольник прямоугольный и равнобедренный. Значит,
, тогда этот треугольник прямоугольный и равнобедренный. Значит,
ВМ = АМ = 8 см.
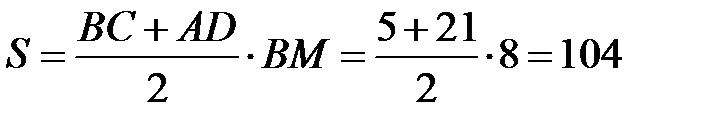 (см2).
(см2).
Ответ: 104 см2.
| Содержание критерия | Баллы |
| Верно получен обоснованный ответ. | |
| Допущена ошибка при нахождении высоты трапеции. ИЛИ Допущена ошибка при нахождении площади трапеции ИЛИ Получен неверный ответ из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения. | |
| Решение не соответствует ни одному из критериев, приведённых выше. | |
| Максимальный балл | 2 |
№ 17. Найдите область определения функции 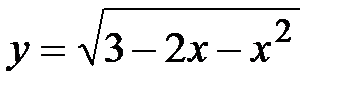 .
.
Решение.
Так как данная функций вида 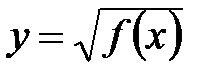 , то
, то 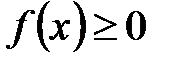 .
.
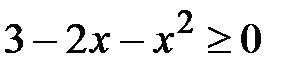 ;
;
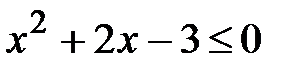 ;
;
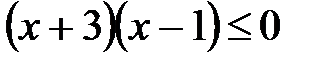 ;
;
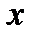
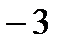
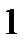
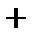
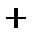
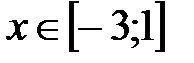
Ответ: 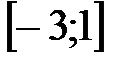 .
.
| Содержание критерия | Баллы |
| Верно получен обоснованный ответ | |
| Допущена ошибка при составлении неравенства ИЛИ Допущена ошибка при решении квадратного неравенства ИЛИ Получен неверный ответ из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения. | |
| Решение не соответствует ни одному из критериев, приведённых выше. | |
| Максимальный балл | 2 |
№ 18. Параллельно оси цилиндрапроведено сечение, которое является квадратом со стороной 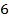 см и отсекает от окружности основания дугу, градусной мерой
см и отсекает от окружности основания дугу, градусной мерой 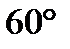 . Найдите площадь боковой поверхности цилиндра.
. Найдите площадь боковой поверхности цилиндра.
Решение.
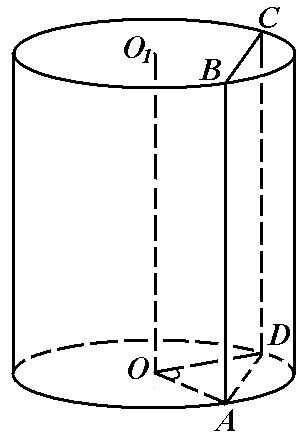
ОО 1 – ось цилиндра, квадрат ABCD – сечение цилиндра, (ABC) || ОО 1.
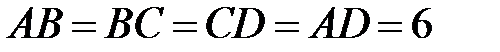 см,
см, 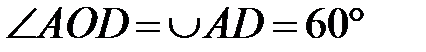 .
.
Тогда 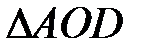 – равносторонний и АО = 6 см.
– равносторонний и АО = 6 см. 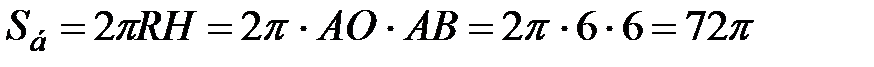 см2.
см2.
Ответ: 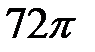 см2.
см2.
| Содержание критерия | Баллы |
| Верно получен обоснованный ответ. | |
| Получен неверный ответ из-за вычислительной ошибки, но при этом имеется верная последовательность и обоснованность всех шагов решения. | |
| Решение не соответствует ни одному из критериев, приведённых выше. | |
| Максимальный балл | 2 |
№ 19. Исследуйте функцию 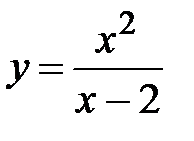 и постройте ее график.
и постройте ее график.
Решение.
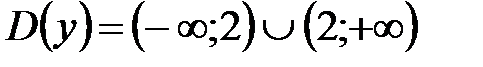 .
.
Точки пересечения с осями координат: 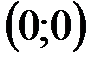 .
.
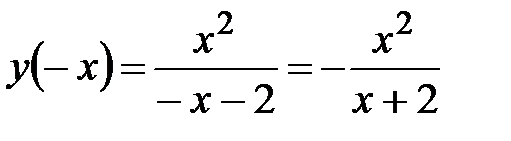 .
.
Так как 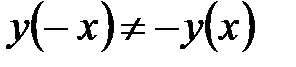 и
и 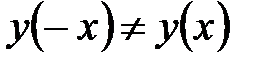 , то функция ни четная, ни нечетная.
, то функция ни четная, ни нечетная.
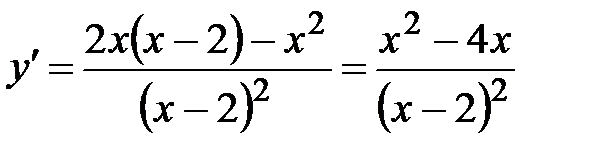 .
.
Стационарные точки: 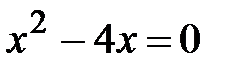 ;
; 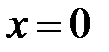 ,
, 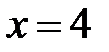 .
.
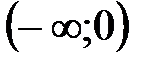
| 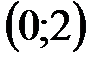
| 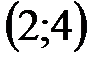
| 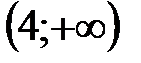
| ||||
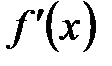
| + | – | – | + | |||
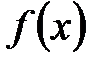
| |||||||
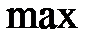
| 
|
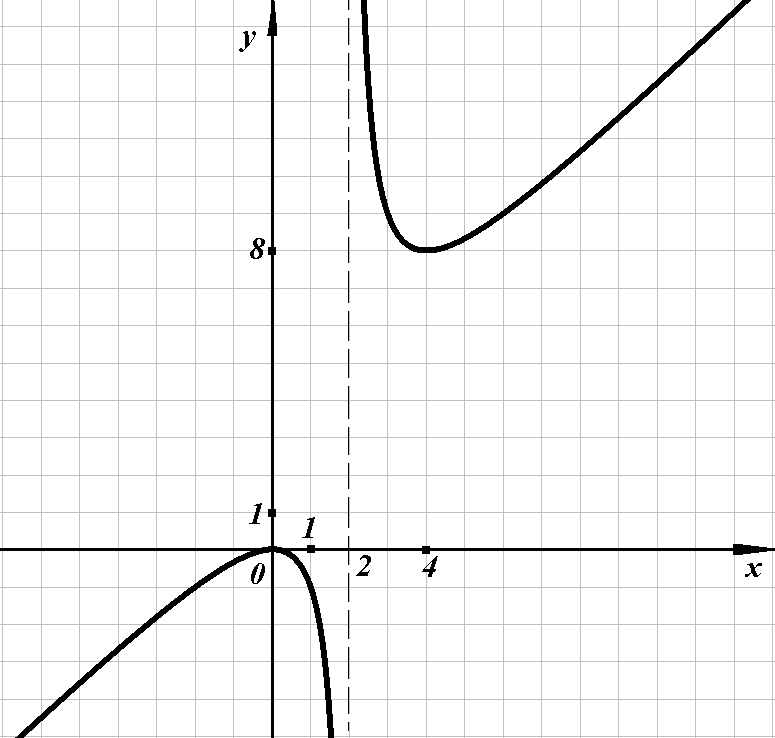 Сделаем рисунок.
Сделаем рисунок.
| Содержание критерия | Баллы |
| Верно исследована функция и верно построен график | |
| Построен верно график, но выполнены не все этапы исследования функции. ИЛИ Построен неверный график, но при этом имеется верная последовательность и обоснованность всех шагов решения ИЛИ Приведено правильное полное исследование функции, но не построен график | |
| Построен верный график, но отсутствует исследование функции ИЛИ Построен неверный график в результате двух и более ошибок при исследовании функции. | |
| Решение не соответствует ни одному из критериев, приведённых выше. | |
| Максимальный балл | 3 |
№ 20 В основании прямой призмы лежит ромб. Большая диагональ призмы равна 12 см и наклонена к плоскости основания под углом 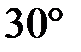 , а меньшая образует с боковым ребром угол
, а меньшая образует с боковым ребром угол 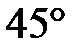 . Найдите объем призмы.
. Найдите объем призмы.
Решение.
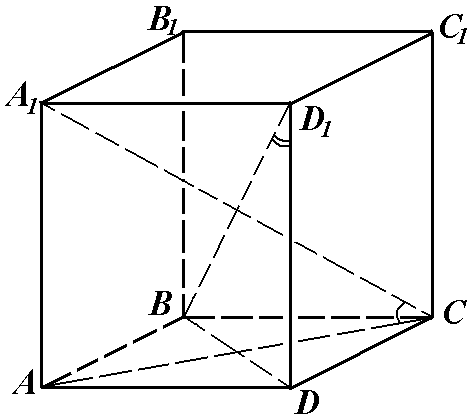 1. Рисунок, пояснения к рисунку.
1. Рисунок, пояснения к рисунку.
ABCDA1B1C1D1 – прямая призма. Ее основание ABCD – ромб, 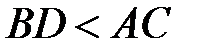 – его диагонали. Высотой призмы является боковое ребро. Тогда
– его диагонали. Высотой призмы является боковое ребро. Тогда 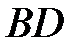 – проекция
– проекция 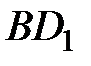 на плоскость основания, АС – проекция А 1 С на плоскость основания. Так как
на плоскость основания, АС – проекция А 1 С на плоскость основания. Так как 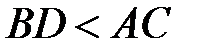 , а
, а 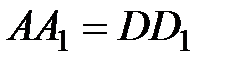 , то
, то 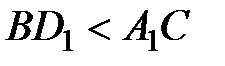 – диагонали призмы и
– диагонали призмы и 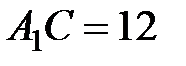 см,
см, 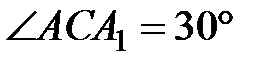 и
и 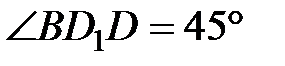 .
.
Найдем объем призмы по формуле:
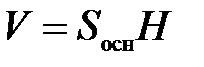 ,
,
где S осн – площадь основания призмы, то есть S осн = SABCD;
Н – высота призмы, то есть Н = АА 1.
2. Нахождение высоты.
Для нахождения высоты рассмотрим 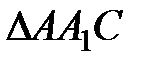 .
.
Из 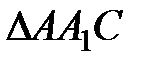 (
(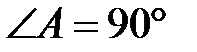 ):
):
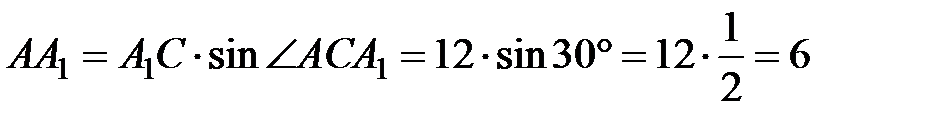 (см), то есть Н = 6 см.
(см), то есть Н = 6 см.
3. Нахождение площади основания.
Площадьоснования призмы найдем по формуле 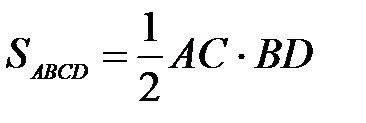 .
.
Для нахождения АС рассмотрим 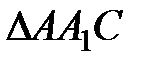 (
(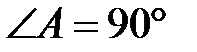 ):
):
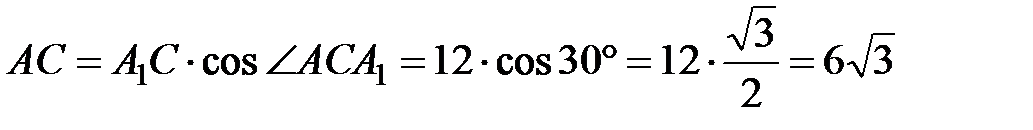 (см).
(см).
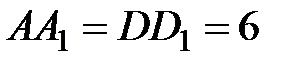 см как боковые ребра призмы.
см как боковые ребра призмы.
Для нахождения BD рассмотрим 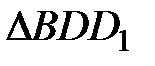 (
(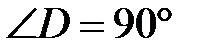 ):
):
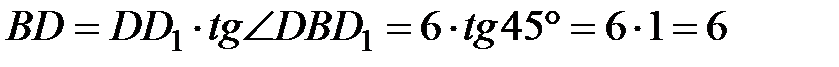 (см).
(см).
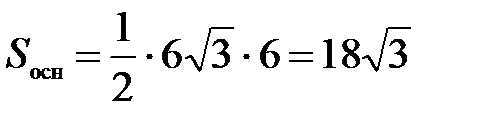 (см2).
(см2).
4. Нахождение объема
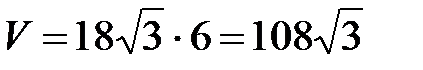 (см3).
(см3).
Ответ: 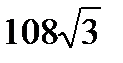 см
см 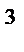 .
.
| Содержание критерия | Баллы |
| 1. Правильно сделан чертеж (показаны диагонали и углы, сделаны пояснения к рисунку). 2. Правильно найдена высота. 3. Правильно найдена площадь основания. 4. Правильно найден объем. | |
| Отсутствует один из критериев оценивания, указанных выше | |
| Допущены ошибки, которые не повлияли на правильный ход решения | |
| Решение не соответствует ни одному из критериев, приведённых выше. | |
| Максимальный балл | 2 |
Максимальный первичный балл за всю работу – 30.
Критерии оценивания
| Отметка | Процент |
| 90 – 100 | |
| 75 – 89 | |
| 60 – 74 | |
| 36 – 59 | |
| 0 – 35 |
Соответствиеколичества набранных баллов, оценке по пятибалльной системе оценивания учебных достижений учащихся приведено в таблице:
| Количество набранных баллов | Оценка по пятибалльной системе оценивания учебных достижений учащихся |
| 27-30 | |
| 22-26 | |
| 18-21 | |
| 10-17 | |
| 0-9 |
Желаем успеха!