Интегральная теорема Лапласа

Схема Бернулли. Биномиальная формула

Несколько раз бросаем монету. Появление герба, скажем, при четвертом бросании не зависит от того, каковы были результаты при первом, при втором и при третьем бросаниях. Мы имеем дело с независимыми испытаниями. Решим теперь такую задачу.

При проведении некоторого однократного испытания вероятность появления события А равна р, а непоявления q= 1— р.

Какова вероятность того, что при n повторных испытаниях событие А произойдет т раз? Это событие запишем так: «S_n = m»

Станем искать P(S_n = m).

Событие, состоящее в том, что при п независимых испытаниях А происходило т раз, а не происходило п—т раз, можем себе представить в виде п клеток, m из которых заполнены буквой А, а п — m— буквой 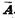. Например, одно из таких представлений, которое назовем событием В₁, может быть таким, как на рисунке.

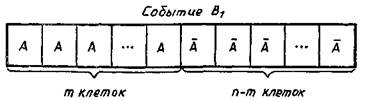
Таких событий, когда m клеток заполнено буквой А, а п—m клеток — буквой может произойти столько, сколько перестановок с повторениями можно построить из m букв А и п —mбукв 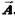. Если число таких событий обозначим N, то по формулам комбинаторики

N =

Нас интересующее событие «S_n=m» представляет собой объединение N событий В₁, В₂, В₃,..., B_N. Они равновозможны и попарно несовместимы, поэтому

P(S_n=m)=P(B_l)+P(B₂) +...+P(B_N) = N*P(B_l).

Но

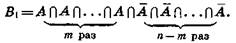
Поскольку испытания независимы в совокупности и Р(А)=р, Р(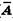)=q, то

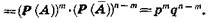
Объединяя полученные результаты, находим формулу Бернулли:

Pn(m) = P(Sn = m) = 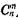p^mq^n-m.

Это так называемое биноминальное распределение вероятностей. Рассуждения, которые к нему привели, часто называют схемой Я. Бернулли, по имени математика, который первым ее рассмотрел.

Наиболее вероятное число наступления события в схеме Бернулли

С помощью полученной формулы можно найти значение S_n = т₀, которому соответствует наибольшая вероятность.

Поскольку 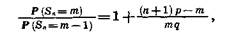то

Р(S_n=m)>P(S_n=m— 1) при т<(п+1)р,
P(S_n=m)<P(S_n=m— 1) при m>(n+1)p,
Р(S_n=m)=P(S_n=m—1) при т = (п+1)р,

если (п+1) р — целое число.

Поэтому вероятнейшее значение S_n = m₀ должно удовлетворить условию

(n + 1)р —1<m₀<(n + 1)р. Поскольку р = 1 — q, то

пр — q<= т₀ <= пр +p.

 

Формула Муавра-Лапласа

Рассмотрим пример: Медиками установлено, что 94% лиц, которым сделаны прививки против туберкулеза, приобретают иммунитет против этого заболевания. Какова вероятность того, что среди 100 000 граждан, получивших прививки, 5800 не защищены от заболевания туберкулезом?

Эту задачу можно было бы решить с помощью формулы Бернулли.

В нашем случае п = 100 000, т = 5800, р = 0,06, <? = 0,94. Если интересующие нас события обозначим А, то

Р(А) = Р(S_{100 000} = 5800)= .(0,06)⁵⁸⁰⁰.(0,94)^{94 200}.

Нетрудно убедиться в том, что попытка получить окончательный результат непосредственным вычислением — изнурительный труд, даже если воспользоваться логарифмами или ЭВМ. Как быть?

Аналогичную проблему рассматривали Муавр и Лаплас. Нет надобности раскрывать перед читателем всю сложность их рассуждений, но маленькое окошко в эту тайну откроем.

Математики того времени знали формулу

C_n^m = = =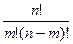

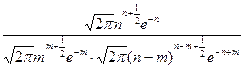C_n^m =

Называлась она формулой Стирлинга, хотя имеются данные, что раньше этого шотландца данную формулу знал Муавр. (Доказательство формулы см. в разделе «комбинаторика» 2 часть)

Локальная теорема Лапласа

Теперь приступим к доказательству локальной теоремы Муавра — Лапласа, особенно не заботясь о строгости самой процедуры доказательства.

Теорема гласит:

Пусть:

1) событие А при отдельном испытании может произойти с вероятностью р, а не произойти с вероятностью q = 1 — р;

2) проведено п независимых испытаний.

Если п и т таковы, что 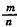- р -> 0, а х = 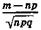есть ограниченная величина при п, стремящемся к бесконечности, то

Pn(m) =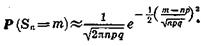

Доказательство.

Известно, что в случае |x| <1 (согласно формуле суммы бесконечной убывающей геометрической прогрессии 1-x+x²-x³+…= )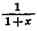

Когда х близко к нулю, можно пользоваться приближенным соотношением

1-х.

Скажем, при x=0,1 левая часть равенства дает результат 0,90909..., а правая — 0,9. При х=— 0,1 левая часть даст 1,111..., а правая — 1,1. Когда х близко к нулю, погрешность будет незначительна, т. е.

ln(l + z) » z—z²/2

Из формулы Бернулли (P(S_n = m)= p^mq^n-m), используя формулу Стирлинга, получаем:

C_n^m = =

Введем обозначение b _m = m — пр.

Значит, т = пр+b_т, п — т = п — пр — b_m = п (1— р)— b _m = nq — b _m.

Заменяя т и п — т полученными аналогами, находим:

P(S_n = m) =

P(S_n = m) =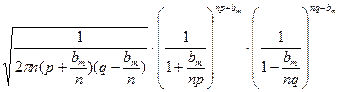

Из условия теоремы m/n— р -> 0 следует, что с возрастанием п, b_m/n —>0.

Знаменатель дроби в скобках обозначаем К(т;n), т. е.

Тогда ln К (m; п) = (пр +b_m+ 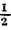)*ln(l + 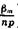) + (nq — b_m + )*ln(l- ).

Поскольку при возрастании п, 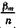->- 0, то ln(l + z) » z—z²/2 в ln(1+ ) и ln(l— ) заменяем их приближенными выражениями:

Приводим подобные члены и группируем по степеням . Получаем:

ln К(m;п) Поскольку p+q =1, то

Но из условий теоремы следует:

1) ->0;

2) 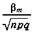ограничено.

Таким образом,

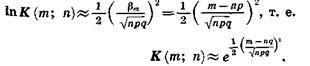
Возвращая полученное значение знаменателя в дробь, получаем, что нужно

Обозначим Тогда Pn(m) =

Функция j (х) используется очень часто и ее значения заранее просчитаны и представлены в статистических таблицах. Образец графика этой функции (см. рис.).

 

 

Формула Пуассона

Формула Муавра — Лапласа базируется на приближенной формуле Стирлинга. Когда р близко к 0 или 1, формула дает результаты, которые существенно отклоняются от результатов, получаемых по формуле Бернулли. Рассмотрим случай, когда при возрастании п вероятность р появления интересующего нас события убывает, a np=k — постоянное число.

Именно такая ситуация возникает, когда имеем дело с редко происходящими событиями.

По формуле Бернулли и условию q = 1— p имеем:

P(S_n = m)=- 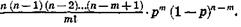Поскольку р= , то

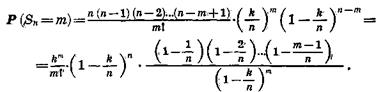
Если обозначим

то

P(S _n = m) = a _n b _n.

Установим предельные значения а _n и b _n при неограниченном возрастании п. Ясно, что

lim b _n = 1, а _n =(1 — 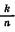)ⁿ = 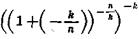Обозначим h = — 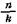. Тогда

Поскольку k >=0, то при п->+ оо, h->— oo

Пусть h +1 = — х, тогда при h->—оо, x->оо. Получаем:

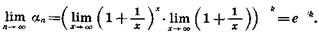
Значит, если п велико, то

a _n » e^-k, b _п » 1.

Подставляя эти значения в (6.13), находим формулу Пуассона:

P(S_n = m) » 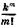e^-k

 

Интегральная теорема Лапласа

 

Решим следующую задачу:

Задача. Какова вероятность того, что при п испытаниях событие А произойдет не менее a и не более bраз? Используя правило сложения вероятностей, имеем:

P(a<=S_n<=b) = P(S_n=a) + P(S_n=a+l) +... + P(S_n=b-l) + P(S_n=b).

Отсюда приступаем к доказательству интегральной теоремы Лапласа, которая гласит: Пусть:

1) событие А при отдельном испытании может произойти с вероятностью р, а не произойти с вероятностью q = 1 — р;

2) проведено п независимых испытаний.

Если п и т таковы, что при п, стремящемся к бесконечности:

а) — р -> 0;

б) 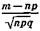есть ограниченная величина, то

P(a£S_n£b) » Ф(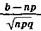) - Ф ()'

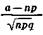где Ф (х) — первообразная функция от j (х), которая была получена выше.

Доказательство.

При обозначениях

По определению первообразной функции Ф (х) имеет место равенство Ф'(x)= j (x).

Пусть = ∆ x = x_i+1—x_i для всех i =1, 2, 3,.... k — 1.

Можем записать:

P(S_n = a) » -, где х₁= ,

P(S_n = a + l) » 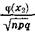, где х₂ =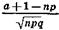

P(S_n = b —1) » , где x_k-1 =

P(S_n = b)) » , где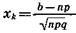

Тогда

Но поскольку Ф'(х)= j (х), то по формуле конечных приращений

j(x₁)∆ x » Ф (х₂)- Ф (х₁)

j(x₂)∆ x » Ф (х₃)- Ф (х₂)

j(x₃)∆ x » Ф (х₄)- Ф (х₃)

…

j(x_k-1)∆ x » Ф (х_k)- Ф (х_k-1)

Подставляя (6.18) в соотношение (6.17), получаем:

Р( a£S_n£b ) »Ф (х₂)- Ф (х₁) + Ф (х₃)- Ф (х₂) +... + Ф (х_k)- Ф (х_k-1) + j(x_k-1)∆ x.

После сокращения подобных членов получим:

Р(а < S_n <b ) » Ф (х_k) - Ф (х₁) + j(x_k-1)∆ x.

Но поскольку ∆х->0, x_k = 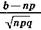и x₁ = 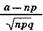, то

Р( a£S_n£b ) » Ф(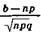) — Ф(),

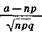что и требовалось доказать.

Функция у = Ф(х), первообразная функции y=j (х), так же широко используется, и в справочниках приводится таблица ее значений.