11.11.2021
Тема: Свободное падение тел. Равномерное движение точки по окружности
Теоретический материал
Свободное падение тел
Одним из наиболее распространенных видов движения с постоянным ускорением - свободное падение тел.
Свободное падение - это движение тел только лишь под действием притяжения Земли (под действием силы тяжести).
При падении тела на Землю из состояния покоя его скорость увеличивается. Земля сообщает телам ускорение, которое направлено вниз вертикально.
При свободном падении все тела вблизи поверхности Земли независимо от их массы приобретают одинаковое ускорение, называемое ускорением свободного падения.
Условное обозначение ускорения свободного падения - g.
На поверхности Земли ускорение свободного падения (g) меняется в пределах от 9,78 м/с2 на экваторе до 9,83 м/с2 на полюсе. При решении многих задач можно принимать g вблизи поверхности Земли равным 9,8 м/с2 или даже более грубо 10 м/с2. При падении тел в воздухе на их движение влияет сопротивление воздуха. Поэтому ускорение тел в этом случае уже не равно g. При больших скоростях сопротивление воздуха существенно и его влиянием нельзя пренебречь.
Ускорение свободного падения всегда направлено к центру Земли и приблизительно равно:
g = 9,81м/с2.
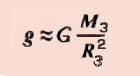
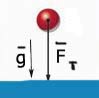
Таким образом, в условиях Земли падение тел считается условно свободным, т.к. при падении тела в воздушной среде всегда возникает еще и сила сопротивления воздуха.
Идеальное свободное падение возможно лишь в вакууме, где нет силы сопротивления воздуха, и независимо от массы, плотности и формы все тела падают одинаково быстро, т. е. в любой момент времени тела имеют одинаковые мгновенные скорости и ускорения.
Составим таблицу
| Равноускоренное движение | Свободное падение тел | Движение тела, брошенного вверх |
| υ= υ 0 + α t | υ= υ 0 + g t | υ= υ 0 - g t |
| υ х= υ 0х + α х t | υ у= υ 0 у+ g у t | υ у = υ 0 у - g у t |
| S= υ 0 t+ α t2/2 | h= υ 0t + gt2/2 | h= υ 0t + gt2/2 |
| S х= υ 0 х t+ α хt2/2 | h= υ 0уt + g уt2/2 | h=υ 0уt - g уt2/2 |
| х=х0 +υ 0 х t+ α хt2/2 | У= У0+ υ 0уt + g уt2/2 | У0=0 |
Вблизи поверхности Земли величина силы тяжести считается постоянной, поэтому свободное падение тела - это движение тела под действием постоянной силы. Следовательно, свободное падение - это равноускоренное движение.
Вектор силы тяжести и создаваемого ею ускорения свободного падения направлены всегда одинаково.
Все формулы для равноускоренного движения применимы для свободного падения тел.
Равномерное движение точки по окружности
4.1. Равномерное движение материальной точки окружности. Линейная скорость.
Движение тела по окружности является частным случаем криволинейного движения.
Движение, при котором материальная точка движется по окружности с постоянной скоростью, называют равномерным движением по окружности.
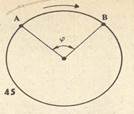Допустим, что материальная точка движется равномерно по окружности и в момент t1 находится в положении А (рис. 1), а в момент t2 точка заняла положение В. Радиус, проведенный из центра окружности к материальной точке, за это время описал угол φ, который называют угловым перемещением.
Угловое перемещение в международной системе единиц выражают в радианах.
Допустим что материальная точка равномерно движется по окружности радиусом R. Так как движение точки равномерное, то модуль скорости постоянен. Например, за очень малое время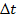 
точка переместилась из положения А1 в положение В1 (на рис. 3 для наглядности перемещение А1 В1 показано увеличенным).
Тогда по общему определению скорости линейная скорость на участке направлена вдоль хорды А1 В1. так как хорда при уменьшении промежутка времени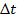 
все более приближается к дуге, то вектор скорости в середине участка А1 В1 (в точке С) направлен по касательной к дуге.
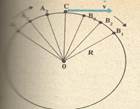
Рисунок 3.
Следовательно, и мгновенная скорость в любой другой точке окружности направлена по касательной. В этом можно убедиться, если прижать к вращательному точильному камню конец стального прутка. Раскаленные частицы, отрывающиеся от камня и летящие с той скоростью, которой они обладали в момент отрыва, будут видны в виде искр.
Направление вылета искр всегда совпадает с касательной к окружности в той точке, где пруток касается камня, по касательной окружности движутся и брызги от колес буксующего автомобиля (рис 4). Таким образом, линейная скорость тела, движущегося по окружности, оставаясь постоянной по модулю, непрерывно изменяется по направлению и в любой точке направлена по касательной к траектории.
Так как модуль линейной скорости постоянен, то его можно определить по формуле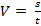 
. За один оборот (
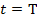) тело пройдет расстояние, равное длине окружности: s = 2πR, или, учтя, что Т = 
, 
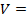2πR.
Найдем отношение линейной скорости к угловой:
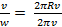= R.
Таким образом, v =wR w = 
4.2. Угловая скорость.
Угловой скоростью ω тела в данной точке круговой траектории называют отношение углового перемещения Δφ к промежутку времени Δt, в течение которого это перемещение произошло.
ω=∆φ/∆t
Угловая скорость измеряется в рад/с. За единицу угловой скорости в Международной системе единиц принята скорость такого равномерного движения тела по окружности, при котором в каждую секунду совершается угловое перемещение в 1 радиан. Эта единица угловой скорости называется радиан в секунду и обозначается 1 рад/с.
Связь между модулем линейной скорости υ и угловой скоростью ω: v =wR
При равномерном движении тела по окружности величины υ и ω остаются неизменными. В этом случае при движении изменяется только направление вектора 
.
4.3. Ускорение при равномерном движении тела по окружности.
При равномерном движении тела по окружности его линейная скорость, оставаясь постоянной по модулю, непрерывно изменяется по направлению. Но изменение скорости по направлению свидетельствует о том, что при равномерном движении тела по окружности есть ускорение, которое и является причиной непрерывного изменения направления скорости. Это ускорение получило название центростремительное.
По определению ускорение характеризует быстроту изменения скорости и равно отношению изменения скорости к промежуточному времени, за которое это изменение произошло, а его направление совпадает с направлением вектора изменения скорости
= 
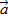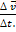, или в скалярной форме 
= 
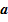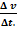
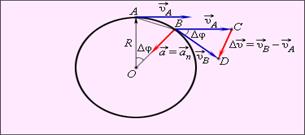
Как найти центростремительное ускорение? Допустим, что тело, равномерно движущееся по окружности, в момент времени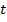 
находилось в точке А (рис.), а через очень малый промежуток времени 
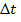переместилось в очень близко расположенную точку В (на рисунке расстояние АВ для наглядности показано увеличенным). Скорость в точке А обозначим 
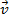A, а в точке В 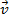В. Модули скорости в точках А и В одинаковы. Для того, чтобы найти изменение скорости за время 
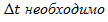вычесть (по правилу треугольника) из вектора 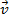В вектор 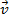А.
∆ = В - А
Векторы скоростей и в точках A и B направлены по касательным к окружности в этих точках. Модули скоростей одинаковы υA = υB = υ.
Из подобия треугольников OAB и BCD (рис.) следует:
= 
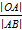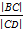
а =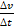 
= 
= 
;
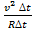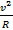Таким образом, при равномерном движении тела (материальной точки) по окружности ускорение в любой точке траектории перпендикулярно скорости движения и направлено к центру окружности. Модуль его равен частному от деления квадрата линейной скорости на радиус вращения.
Итак, равномерное движение тела по окружности является движением с ускорением. Модуль ускорения а =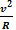 
направлено по радиусу к центру окружности. Его называют центростремительным ускорением. Модуль центростремительного ускорения связан с линейной υ и угловой ω скоростями соотношениями: а = 
= 
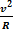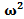R
При изменении положения тела на окружности изменяется направление скорости и ускорения. При равномерном движении тела по окружности модуль ускорения остается неизменным, но направление вектора ускорения изменяется со временем.
4.4. Частота и период обращения.
Частотой обращения называют число оборотов материальной точки вокруг центра обращения за секунду. Частоту обращения принято обозначать греческой буквой v (ню):
v = 
где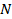 
- число оборотов, совершенных за время 
. За единицу частоты в международной системе единиц 1 оборот в секунду. Его сокращенное обозначение – 1 с -1.
Периодом обращения называется время, в течение которого совершается один оборот точки по окружности. Период обозначают буквой Т:
Т = 
За единицу периода в международной системе единиц принята секунда - 1 с. Нетрудно заметить, что период и частота – величины взаимно обратные:
v = 
Т = 
Разбор решения задач
Задача 1.