Линейные однородные дифференциальные уравнения

Линейная независимость функций. Определитель Вронского.

Бесконечно дифференцируемые функции образуют линейное пространство. Поэтому для них существуют понятия линейной зависимости и независимости. Например, тождество устанавливает линейную зависимость функций . Однако, тождество не является линейной комбинацией, поэтому с его помощью нельзя решить вопрос о линейной зависимости функций .

Простейшие признаки линейной зависимости, действуют в случае функций, как и в любом линейном пространстве. А именно, система функций линейно зависима, если:

1. Она содержит функцию, тождественно равную нулю.

2. Она содержит две пропорциональные (в частности, равные) функции.

Доказательство линейной независимости функций удобнее всего проводить с помощью определителя Вронского

(аргументы х опущены для удобства записи).

Теорема 1. Если определитель Вронского хотя бы при одном значении х не равен нулю, система функций линейно независима.

Линейные однородные дифференциальные уравнения с переменными коэффициентами

Дифференциальное уравнение вида

называется линейным однородным дифференциальным уравнением n-го порядка. Если функции определены и непрерывны на промежутке (a, b), то общее решение также определено на (a, b) и представляет собой линейную комбинацию n линейно независимых частных решений с произвольными коэффициентами.

Система функций называется фундаментальной системой решений (ФСР) линейного однородного дифференциального уравнения. Заметим, что ФСР определена неоднозначно.

В частности линейное однородное дифференциальное уравнение 2-го порядка

имеет общее решение вида , где 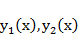– не пропорцио-нальные друг другу частные решения.

Теорема 2. Если – фундаментальная система решений линейного однородного дифференциального уравнения, то определитель Вронского не обращается в ноль ни в одной точке.

Если для линейного однородного дифференциального уравнения известно ненулевое частное решение , порядок уравнения может быть понижен с помощью подстановки . Она приводит к линейному однородному уравнению для , не содержащему неизвестную функцию в явном виде. Далее делается замена .

Для уравнений 2-го порядка указанный прием позволяет найти общее решение уравнения при известном частном решении . (См. задачи 2, 3).

Линейные однородные дифференциальные уравнения 2-го порядка с постоянными коэффициентами

Дифференциальное уравнение вида

`

где ­– постоянные, называется линейным однородным дифференциальным уравнением 2-го порядка с постоянными коэффициентами. (Как правило, в примерах а =1.) Фундаментальная система решений такого дифференциального уравнения связана с алгебраическим уравнением 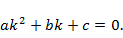Оно называется характеристическим уравнением, а его корни – характеристическими корнями. Возможные варианты описаны в таблице 1.

Таблица 1

Характеристические корни	ФСР	Общее решение
Действительные различные
Действительный кратности 2
Комплексные

Отметим, что последний случай возникает, когда дискриминант характеристического уравнения 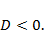В этом случае для удобства принимают

Линейные однородные уравнения n -го порядка с постоянными коэффициентами

Линейное однородное дифференциальное уравнение n-го порядка с постоянными коэффициентами имеет вид

Решение таких уравнений происходит аналогично случаю n =2. Отличия состоят в том, что у характеристического уравнения могут возникнуть корни кратности выше 2, а при n ≥4 – кратные комплексные корни. Возможные варианты описаны в таблице 2. Во втором столбце этой таблицы символом обозначено количество линейно независимых частных решений, соответствующих данному действительному корню или данной паре комплексных корней. В третьем столбце таблицы эти решения перечислены через точку с запятой (без указания их порядковых номеров).

Таблица 2

Характеристические корни		Частные решения, входящие в ФСР
Простой действительный корень k
Пара простых комплексных корней
Действительный корень k кратности r	r
Пара комплексных корней кратности r	2 r