Дифференциальные уравнения, допускающие понижение порядка.
Обыкновенное дифференциальное уравнение (ОДУ) 2-го порядка в общем виде задается формулой
F (x, y, y’, y”) = 0,
а в виде, разрешенном относительно старшей производной – формулой
y” = f (x, y, y’).
Задачей Коши для обыкновенного дифференциального уравнения называется задача поиска решения y (x), удовлетворяющего начальным условиям
у (х 0) = у 0, у’ (х 0) = у 1.
Общим решением уравнения 2-го порядка называется зависимость у = j (x, С 1, С 2) такая что:
1) При фиксации любых допустимых значений С 1, С 2 получается решение ОДУ.
2) Для любых начальных условий найдутся единственные значения С 1, С 2, такие что зависимость у = j (x, С 1, С 2)– решение задачи Коши с этими начальными условиями.
Общих методов интегрирования ОДУ 2-го порядка нет. Иногда удается свести задачу к интегрированию ОДУ 1-го порядка. В этих случаях говорят, что ОДУ допускает понижение порядка. Ниже рассмотрены два основных типа таких ОДУ.
При решении задачи Коши не всегда целесообразно находить общее решение. Как правило, удобнее определять значение константы, возникшей при первом взятии интеграла, сразу. Это позволяет в дальнейшем обойтись без вычисления интеграла, зависящего от параметра. Примеры см. в задаче 3.
Уравнения без явной зависимости от у.
Если ОДУ 2-го порядка имеет вид y” = f (x, y’), то с помощью замены 
его можно преобразовать в ОДУ 1-го порядка 
. Найдя общее решение вспомогательного уравнения 
, далее интегрированием находят
Автономные уравнения
Автономным называется уравнение, не содержащее явно независимой переменной. Такие уравнения часто возникают на практике, если закон изменения величины по времени действует одинаково во все моменты времени.
Понижение порядка автономного ОДУ 
происходит следующим образом. Рассматривается зависимость между скоростью изменения неизвестной величины и ее текущим значением: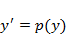 
. Выражение для y ” получается по правилу дифференцирования сложной функции:
Таким образом, получается ОДУ 1-го порядка 
с независимой переменной у. После того, как в его общем решении 
сделана обратная замена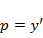 
, возникает уравнение с разделяющимися переменными
После интегрирования получается общее решение исходного ОДУ в неявном виде:
Эта основная формула, возможно, нуждается в следующем дополнении: если 
, имеется постоянное решение 
Решение типовых задач
Задача 1. Найти общие решения ОДУ 2-го порядка, не зависящих явно от у.
a1) 
Решение. Замена 
приводит к линейному уравнению 1-го порядка
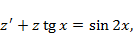
которое интегрируется подстановкой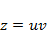 
:
Отсюда получаем общее решение:
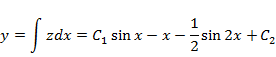
b1)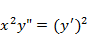 
Решение. Замена приводит к уравнению 1-го порядка с разделяющимися переменными
Если z =0, то 
откуда 
При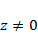 
разделяем переменные и выполняем интегрирование:
Знак минус, поставленный перед константой, позволяет избавиться от минусов в следующей формуле.
Взятие последнего интеграла происходит по-разному при 
и при 
. В первом случае 
Во втором случае
Таким образом, общее решение описывается тремя формулами:
Задача 2. Найти общие решения автономных ОДУ 2-го порядка.
b1)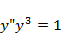 
Решение. Замена 
приводит к уравнению 1-го порядка с разделяющимися переменными
Можно упростить формулу, переобозначив константу: если 
, то
Отметим, что здесь 
, так как обе части уравнения неотрицательны. Отсюда
Снова разделим переменные и проинтегрируем:
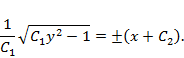
Осталось преобразовать ответ к наиболее удобной форме:
b2) 
Решение. Замена приводит к уравнению 1-го порядка
Отдельного рассмотрения требует случай 
При этом откуда
Если 
то его можно сократить. При этом получится уравнение с разделяющимися переменными 
Далее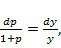 
следовательно 
Для неизвестной функции 
имеем уравнение 
Если 
то 
При расчет происходит следующим образом:
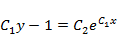
(переобозначение константы и снятие модуля делается так же, как в задачах предыдущего раздела).
Задача 3. Найти решения задач Коши.
a1) 
Решение. Замена приводит к задаче Коши для однородного ОДУ 1-го порядка
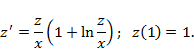
После подстановки 
становится возможным разделение переменных:
Из условия 
можно определить 
:
Таким образом, на последнем этапе решения, мы будем интегрировать не общую формулу 
, а более простую формулу 
. Из нее легко находим, что 
. Из начального условия 
определяем значение 
. Искомое частное решение задачи Коши: 
.
b1) 
Решение. Замена 
приводит к задаче Коши для ОДУ 1-го порядка:
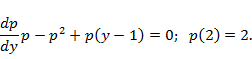
Начальное условие во вспомогательной задаче имеет указанный вид, поскольку при одном и том же значении х одновременно выполнены равенства 
.Начальное условие позволяет сократить р. После этого возникает линейное неоднородное ОДУ
Оно интегрируется подстановкой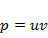 
(разумеется, и и v зависят от у).
Из начального условия вспомогательной задачи получаем: 
. Отсюда . Интегрируя уравнение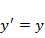 
с начальным условием 
, получаем ответ: 
.
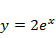Задача 4. Свести к ОДУ 1-го порядка уравнение Ньютона
где 
Дать механическую интерпретацию.
Решение. Уравнение Ньютона – частный случай автономного уравнения. Замена 
приводит к уравнению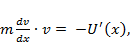 
которому можно придать вид 
Отсюда 
Механическая интерпретация: x –координата материальной точки в момент времени t, m – ее масса, v – скорость. ОДУ представляет собой математическую запись 2-го закона Ньютона, если на точку действует потенциальная сила. Последняя формула в решении – закон сохранения энергии: 
Задачи для самостоятельного решения
Задача 5. Найти общие решения ОДУ.
a1) 
a2) 
b1) 
b2) 
b3) 
c1) 
c2) 
c3) 
Задача 6. Найти решения задач Коши.
a1) 
b1) 
b2) 
b3) 
Задача 7. Тело массы т начинает падать с высоты Н без начальной скорости. Сила сопротивления воздуха пропорциональна квадрату скорости тела (коэффициент пропорциональности k известен). На какой высоте окажется тело в момент времени t?