Дифференциальное уравнение вида

называется линейным неоднородным дифференциальным уравнением n-го порядка. Если функции 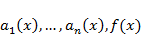 определены и непрерывны на промежутке (a, b), то общее решение также определено на (a, b) и представимо в виде
определены и непрерывны на промежутке (a, b), то общее решение также определено на (a, b) и представимо в виде

где 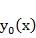 – общее решение соответствующего линейного однородного дифференциального уравнения
– общее решение соответствующего линейного однородного дифференциального уравнения

а  – частное решение неоднородного уравнения. Если ФСР однородного уравнения известна, общее решение неоднородного уравнения можно найти методом вариации постоянных. Для неоднородных уравнений с постоянными коэффициентами и правой частью специального вида применяется также метод неопределенных коэффициентов.
– частное решение неоднородного уравнения. Если ФСР однородного уравнения известна, общее решение неоднородного уравнения можно найти методом вариации постоянных. Для неоднородных уравнений с постоянными коэффициентами и правой частью специального вида применяется также метод неопределенных коэффициентов.
Линейные неоднородные дифференциальные уравнения с постоянными коэффициентами и правой частью специального вида
Класс функций специального вида составляют следующие функции:
1. Показательные 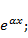
2. Тригонометрические 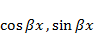 (тангенсы и котангенсы сюда не входят);
(тангенсы и котангенсы сюда не входят);
3. Многочлены (в том числе постоянные);
4. Суммы и произведения (но не частные!) функций, перечисленных выше.
Другими словами, это такие функции, которые могут совпасть с частными решениями линейного однородного дифференциального уравнения с постоянными коэффициентами.
Теорема 3. Если в линейном неоднородном дифференциальном уравнении

правая часть является функцией специального вида, такое уравнение имеет частное решение специального вида.
Назовем квазимногочленом функцию вида  , где
, где  – многочлены степеней k и l соответственно. Назовем его степенью – число
– многочлены степеней k и l соответственно. Назовем его степенью – число  , а показателем – комплексное число
, а показателем – комплексное число  Напомним, что однородное уравнение, соответствующее данному неоднородному, решается с помощью характеристических корней. Эти понятия позволяют сформулировать правила поиска частного решения, уточняющие теорему 3.
Напомним, что однородное уравнение, соответствующее данному неоднородному, решается с помощью характеристических корней. Эти понятия позволяют сформулировать правила поиска частного решения, уточняющие теорему 3.
Правило 1. Если показатель правой части 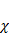 не совпадает ни с одним из характеристических корней, искомое частное решение
не совпадает ни с одним из характеристических корней, искомое частное решение  является квазимногочленом степени m c показателем
является квазимногочленом степени m c показателем 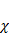 . (См. задачу 1.)
. (См. задачу 1.)
Правило 2. Если показатель правой части 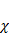 совпадает с характеристическим корнем кратности r, искомое частное решение
совпадает с характеристическим корнем кратности r, искомое частное решение  является произведением квазимногочлена степени m c показателем
является произведением квазимногочлена степени m c показателем 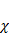 и сомножителя
и сомножителя  (См. задачу 2).
(См. задачу 2).
Правило 3. Если правая часть  где
где  – частное решение уравнения
– частное решение уравнения  ,
, 
Последнее правило используют, если правая часть содержит слагаемые с разными показателями. Оно легко обобщается на любое количество слагаемых (см. задачу 3).
Метод вариации постоянных
Разберем метод вариации постоянных применительно к линейным неоднородным дифференциальным уравнениям 2-го порядка. Напомним, что в этом случае линейное однородное уравнение

имеет общее решение вида  . Общее решение неоднородного уравнения
. Общее решение неоднородного уравнения

будем искать в виде  где
где  – неизвестные функции. Их производные
– неизвестные функции. Их производные  удовлетворяют следующей системе линейных алгебраических уравнений
удовлетворяют следующей системе линейных алгебраических уравнений

Основным определителем этой системы является определитель Вронского  поэтому система однозначно разрешима. С помощью формул Крамера можно получить для
поэтому система однозначно разрешима. С помощью формул Крамера можно получить для  следующие выражения
следующие выражения
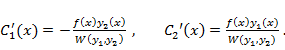
Отметим, что эти формулы проще вывести, чем запомнить. Кроме того, систему линейных алгебраических уравнений не всегда целесообразно решать методом Крамера.
Далее интегрированием находят  . Заметим, что при этом способе решения задачи нет необходимости отдельно указывать частное решение
. Заметим, что при этом способе решения задачи нет необходимости отдельно указывать частное решение  .
.
Аналогично, в случае линейного неоднородного дифференциального уравнения n -го порядка общее решение ищут в виде  Неизвестные функции находят, решая систему линейных алгебраических уравнений
Неизвестные функции находят, решая систему линейных алгебраических уравнений




с последующим интегрированием.
Отметим, что при n =1 метод вариации постоянных совпадает (с точностью до обозначений) с методом Бернулли.
Решение типовых задач
Задача 1. Решить дифференциальные уравнения:
a1) 
Решение. Характеристическое уравнение  поэтому
поэтому  Будем искать
Будем искать  в виде
в виде 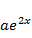 . Тогда
. Тогда  . Подставляя эти выражения в дифференциальное уравнение, получим
. Подставляя эти выражения в дифференциальное уравнение, получим  откуда
откуда  . Общее решение
. Общее решение 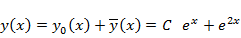 .
.
a2)  .
.
Решение. Характеристическое уравнение  поэтому
поэтому 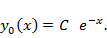 Будем искать
Будем искать  в виде
в виде  . Тогда
. Тогда  . Подставляя эти выражения в дифференциальное уравнение и сгруппировав слагаемые по степеням
. Подставляя эти выражения в дифференциальное уравнение и сгруппировав слагаемые по степеням  , получим
, получим  тсюда
тсюда  . Таким образом,
. Таким образом,  Общее решение
Общее решение 
a3)  .
.
Решение. Характеристический 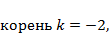 поэтому
поэтому 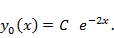 При дифференцировании синуса появится косинус (и наоборот), поэтому
При дифференцировании синуса появится косинус (и наоборот), поэтому  . Подстановка этих выражений в дифференциальное уравнение приводит к соотношению
. Подстановка этих выражений в дифференциальное уравнение приводит к соотношению

из которого вытекает система алгебраических уравнений на неизвестные коэффициенты:  . Решая эту систему, находим
. Решая эту систему, находим 
 . Общее решение
. Общее решение  .
.
b1) 
Решение. Характеристический  поэтому
поэтому  .Показатель правой части
.Показатель правой части  не совпадает с характеристическим корнем, степень m =0. Частное решение ищем в виде
не совпадает с характеристическим корнем, степень m =0. Частное решение ищем в виде  . Дифференцируя, получаем
. Дифференцируя, получаем
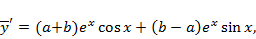

Отсюда

Из системы линейных алгебраических уравнений  находим
находим  . Общее решение
. Общее решение

b2) 
Решение. Характеристические  поэтому
поэтому  .Показатель правой части
.Показатель правой части 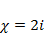 не совпадает с характеристическим корнем, степень m =max(1;0)=1. Частное решение ищем в виде
не совпадает с характеристическим корнем, степень m =max(1;0)=1. Частное решение ищем в виде  . Дифференцируя, получаем
. Дифференцируя, получаем
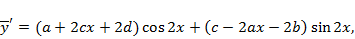

Отсюда

Приравнивая подобные члены в правой и левой частях последнего тождества, получаем уравнения  . Отсутствие в правой части членов вида
. Отсутствие в правой части членов вида  приводит к уравнениям
приводит к уравнениям  . Из этих четырех уравнений находим
. Из этих четырех уравнений находим  . Общее решение
. Общее решение

Замечание. То, что b и с оказались равны нулю, создает впечатление, что можно было бы заранее исключить соответствующие слагаемые из записи  . Этого, вообще говоря, делать не следует, как показывает следующий пример.
. Этого, вообще говоря, делать не следует, как показывает следующий пример.
c1) 
Решение. Характеристические  поэтому
поэтому  .Для
.Для  ” используем те же выражения, что и в предыдущем примере. Их подстановка в дифференциальное уравнение приводит к тождеству
” используем те же выражения, что и в предыдущем примере. Их подстановка в дифференциальное уравнение приводит к тождеству


или, после упрощений

Отсюда получаем систему алгебраических уравнений


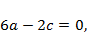
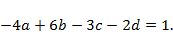
Из первого и третьего уравнения находим  После этого второе и четвертое уравнения принимают вид
После этого второе и четвертое уравнения принимают вид


Отсюда  . (Таким образом,
. (Таким образом,  содержит слагаемые всех четырех типов.) Общее решение
содержит слагаемые всех четырех типов.) Общее решение 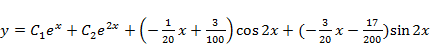 .
.
Задача 2. Решить дифференциальные уравнения:
a1) 
Решение. Характеристический  поэтому
поэтому  . (Отметим, что вследствие этого искать частное решение неоднородного уравнения в виде
. (Отметим, что вследствие этого искать частное решение неоднородного уравнения в виде  бесполезно. Хотите убедиться – попробуйте!) Поскольку показатель
бесполезно. Хотите убедиться – попробуйте!) Поскольку показатель 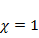 совпадает с характеристическим корнем кратности
совпадает с характеристическим корнем кратности  , будем искать
, будем искать  в виде
в виде  . При этом
. При этом  . Следовательно,
. Следовательно,  , то есть а =1. Общее решение
, то есть а =1. Общее решение 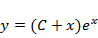 .
.
a2)  .
.
Решение. Характеристические  поэтому
поэтому  .Показатель правой части
.Показатель правой части 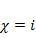 совпадает с характеристическим корнем, поэтому частное решение ищем в виде
совпадает с характеристическим корнем, поэтому частное решение ищем в виде  . Далее,
. Далее,
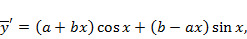

После подстановки этих выражений в дифференциальное уравнение слагаемые с сомножителем  сократятся (проверьте!) Останется равенство
сократятся (проверьте!) Останется равенство
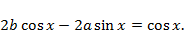
Отсюда  . Общее решение
. Общее решение  .
.
a3)  .
.
Решение. Характеристическое уравнение 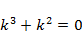 имеет корни
имеет корни  . Значит,
. Значит,  Степень правой части m =1, а показатель
Степень правой части m =1, а показатель 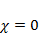 совпадает с корнем кратности r =2. Поэтому частное решение ищем в виде
совпадает с корнем кратности r =2. Поэтому частное решение ищем в виде  . Дифференцируя, находим
. Дифференцируя, находим  затем
затем  и, наконец,
и, наконец,  Отсюда
Отсюда  Из алгебраических уравнений
Из алгебраических уравнений  находим
находим 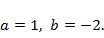 Общее решение
Общее решение 
b1) 
Решение. Характеристические  Степень правой части m =1, показатель
Степень правой части m =1, показатель 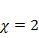 совпадает с корнем кратности r =1. Поэтому частное решение ищем в виде
совпадает с корнем кратности r =1. Поэтому частное решение ищем в виде  Вычисляем производные:
Вычисляем производные:

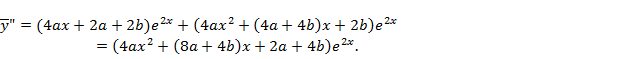
Подстановка этих выражений в дифференциальное уравнение дает:
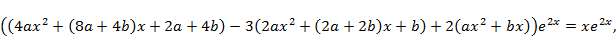
или, после упрощений

Отсюда  . Общее решение
. Общее решение 
c1) 
Решение 1. Характеристические  поэтому
поэтому 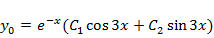 .Показатель правой части
.Показатель правой части  совпадает с характеристическим корнем кратности r =1, степень m =0. Поэтому ищем частное решение в виде
совпадает с характеристическим корнем кратности r =1, степень m =0. Поэтому ищем частное решение в виде  Дифференцируем:
Дифференцируем:


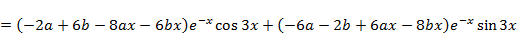
Подстановка этих формул в дифференциальное уравнение приведет к весьма громоздкому выражению. Чтобы не запутаться в выкладке, отдельно сгруппируем члены, которые умножаются на  , опустив этот сомножитель:
, опустив этот сомножитель:

Аналогично сгруппируем сомножители при  :
:

Отсюда получаем  Таким образом,
Таким образом,  Общее решение
Общее решение 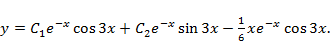
Решение 2 (метод комплексной экспоненты). Рассмотрим вспомогательное дифференциальное уравнение  где
где  –функция с комплексными значениями,
–функция с комплексными значениями,  Характеристическим
Характеристическим  соответствует комплекснозначная ФСР однородного уравнения
соответствует комплекснозначная ФСР однородного уравнения  Поскольку
Поскольку  , будем искать комплексное частное решение в виде
, будем искать комплексное частное решение в виде 
 (аналогично примерам a1 и b1). Тогда
(аналогично примерам a1 и b1). Тогда 
Подставим эти выражения в левую часть дифференциального уравнения и упростим полученную формулу:

Поскольку 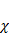 – корень характеристического уравнения, последнее выражение равняется
– корень характеристического уравнения, последнее выражение равняется 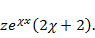 Далее, приравнивая выражения в левой и правой частях ОДУ, находим z:
Далее, приравнивая выражения в левой и правой частях ОДУ, находим z:
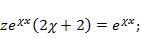

Комплексное частное решение 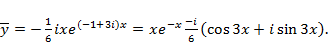
Правые части исходного вещественного и вспомогательного комплексного ОДУ связаны тождеством:  Поэтому
Поэтому  является частным решением исходного уравнения.
является частным решением исходного уравнения.
Задача 3. Решить дифференциальные уравнения:
b1) 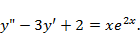
Решение. Внешнее сходство с примером b1 предыдущей задачи не должно вводить в заблуждение. Чтобы выявить структуру общего решения, перепишем уравнение в виде  В правой части оказались слагаемые с разными показателями, поэтому, согласно правилу 3, будем искать общее решение в виде
В правой части оказались слагаемые с разными показателями, поэтому, согласно правилу 3, будем искать общее решение в виде  Характеристические
Характеристические  поэтому
поэтому  .
.
Из того что 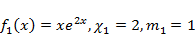 следует, что
следует, что 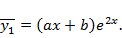 Значит,
Значит,  Подставим эти выражения в левую часть преобразованного ОДУ и приравняем к
Подставим эти выражения в левую часть преобразованного ОДУ и приравняем к 

После упрощений получим

Из алгебраических уравнений 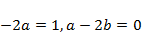 находим
находим  Таким образом,
Таким образом, 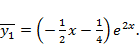
Далее,  Отсюда
Отсюда  Аналогично предыдущему случаю, подставим эти выражения в левую часть преобразованного ОДУ и приравняем к
Аналогично предыдущему случаю, подставим эти выражения в левую часть преобразованного ОДУ и приравняем к  Получим
Получим  Общее решение
Общее решение 
b2) 
Решение. Правая часть преобразуется в сумму квазимногочленов с помощью тригонометрического тождества  . Кратный характеристический корень
. Кратный характеристический корень  Для
Для  вид частного решения
вид частного решения 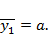 Легко видеть, что
Легко видеть, что  , поскольку
, поскольку 
Для  показатель
показатель  не совпадает с характеристическим корнем, степень
не совпадает с характеристическим корнем, степень  Поэтому
Поэтому 
 Отсюда
Отсюда

Легко находим, что 
Таким образом, общее решение 
Задача 4. В горизонтальном желобе находится идеальная пружина жесткости k. Левый конец пружины зафиксирован, а к правому – прикреплен груз массы m, который может перемещаться по желобу без трения. К грузу приложена сила, периодически зависящая от времени:  . При какой частоте
. При какой частоте  амплитуда колебаний будет неограниченно расти?
амплитуда колебаний будет неограниченно расти?
Решение. Аналогично задаче 4 параграфа 7.3, составим дифференциальное уравнение движения груза:  и перепишем его в виде
и перепишем его в виде

Характеристические корни 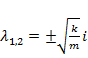 , общее решение однородного уравнения
, общее решение однородного уравнения

является ограниченной функцией. Вид и свойства частного решения неоднородного уравнения  зависят от показателя правой части
зависят от показателя правой части  . При
. При  частное решение
частное решение  независимо от точных значений a и b также является ограниченной функцией. Однако, при совпадении
независимо от точных значений a и b также является ограниченной функцией. Однако, при совпадении 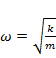 частное решение имеет вид
частное решение имеет вид 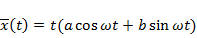 и является неограниченным. Физики называют это явление резонансом. Поскольку сумма ограниченной и неограниченной функций является неограниченной, амплитуда колебаний будет расти независимо от начальных условий.
и является неограниченным. Физики называют это явление резонансом. Поскольку сумма ограниченной и неограниченной функций является неограниченной, амплитуда колебаний будет расти независимо от начальных условий.
Ответ. 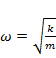 .
.
Задача 5. Не вычисляя неопределенных коэффициентов, указать вид частных решений ОДУ:
a1) 
Решение. Характеристический корень  имеет кратность r =2, показатель правой части
имеет кратность r =2, показатель правой части  совпадает с характеристическим корнем, степень m =1. Вид частного решения
совпадает с характеристическим корнем, степень m =1. Вид частного решения  .
.
b1) 
Решение. Характеристические корни  имеют кратность r =1, показатель правой части
имеют кратность r =1, показатель правой части  совпадает с характеристическим корнем, степень m =2. Вид частного решения
совпадает с характеристическим корнем, степень m =2. Вид частного решения

b2) 
Решение. Характеристическое уравнение может быть записано как  Характеристические корни
Характеристические корни  и
и  имеют кратность r =2, показатель правой части
имеют кратность r =2, показатель правой части 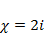 не совпадает с характеристическим корнем, степень m =1. Вид частного решения
не совпадает с характеристическим корнем, степень m =1. Вид частного решения 
c1) 
Решение. Характеристическое уравнение преобразуется к виду  Характеристические корни
Характеристические корни  и
и  имеют кратности 1 и 3 соответственно. Правая часть преобразуется в сумму
имеют кратности 1 и 3 соответственно. Правая часть преобразуется в сумму  Степени обоих слагаемых равны 1. Показатель первого слагаемого
Степени обоих слагаемых равны 1. Показатель первого слагаемого  совпадает с трехкратным характеристическим корнем, показатель второго слагаемого
совпадает с трехкратным характеристическим корнем, показатель второго слагаемого 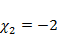 с характеристическими корнями не совпадает. Вид частного решения
с характеристическими корнями не совпадает. Вид частного решения  , где
, где 
Задача 6. Решить задачи с начальными условиями:
a1)  (краевая задача).
(краевая задача).
Решение. Характеристические 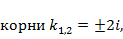 поэтому
поэтому 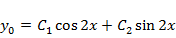 . Вид частного решения
. Вид частного решения 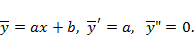 Отсюда
Отсюда  следовательно
следовательно  . Общее решение неоднородного уравнения
. Общее решение неоднородного уравнения

Подставляя сюда  , найдем
, найдем  . Подставляя
. Подставляя  , получим
, получим  , откуда
, откуда  . Искомое решение
. Искомое решение 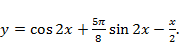
b1)  (задача Коши).
(задача Коши).
Решение. Характеристические  поэтому
поэтому  . Далее,
. Далее, 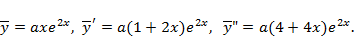 Упрощая соотношение
Упрощая соотношение

получим  Следовательно, общее решение
Следовательно, общее решение  .
.
Подставив в общее решение значения 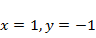 , получим
, получим

Чтобы найти второе соотношение между  и
и  , продифференцируем общее реше-ние:
, продифференцируем общее реше-ние:  и подставим
и подставим  . Получим
. Получим 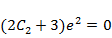 , откуда
, откуда  . Теперь можно вычислить
. Теперь можно вычислить  . Окончательно получаем
. Окончательно получаем 
Замечание. Вычисление констант  в задачах с начальными условиями возможно только после того, как получено общее решение линейного неоднородного уравнения.
в задачах с начальными условиями возможно только после того, как получено общее решение линейного неоднородного уравнения.
Задача 7. Решить дифференциальные уравнения
a1) 
Решение. Правая часть не является функцией специального вида, поэтому задачу нужно решать методом вариации постоянных. ФСР однородного уравнения образуют функции  , поэтому ищем общее решение неоднородного уравнения в виде
, поэтому ищем общее решение неоднородного уравнения в виде  . Из системы
. Из системы


найдем  ,
,  . Из первого уравнения
. Из первого уравнения 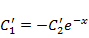 . Подставляя это выражение во второе уравнение, получим
. Подставляя это выражение во второе уравнение, получим  . Отсюда
. Отсюда

Далее находим функции 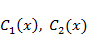 интегрированием:
интегрированием:


(В выкладках подобного рода константы интегрирования обозначают той же буквой, что и искомые функции.) Таким образом,

Ответ можно записать короче, введя константу  Тогда
Тогда
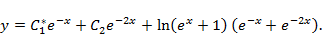
b1) 
Решение. ФСР однородного уравнения образуют функции  , поэтому ищем общее решение неоднородного уравнения в виде
, поэтому ищем общее решение неоднородного уравнения в виде  . Из системы
. Из системы


найдем  ,
,  . Сложив первое уравнение, умноженное на
. Сложив первое уравнение, умноженное на  , со вторым уравнением, умноженным на
, со вторым уравнением, умноженным на  , получим
, получим  Из первого уравнения
Из первого уравнения  Далее
Далее


Общее решение  или
или

Задача 8. Убедившись, что функции  образуют ФСР линейного однородного ОДУ
образуют ФСР линейного однородного ОДУ  , найти общее решение уравнения
, найти общее решение уравнения 
Решение. Проверка первого утверждения – несложное вычисление, которое мы оставляем читателю. Чтобы применить метод вариации к неоднородному уравнению, нужно учесть следующий нюанс: система для определения  записывается в предположении, что коэффициент при старшей производной в неоднородном уравнении равен единице. Поэтому функция в правой части второго уравнения этой системы равна х -1, а не (х -1)2. В остальном запись системы несложна:
записывается в предположении, что коэффициент при старшей производной в неоднородном уравнении равен единице. Поэтому функция в правой части второго уравнения этой системы равна х -1, а не (х -1)2. В остальном запись системы несложна:


Решим эту систему с помощью формул (7.4.1). Найдем  . Далее
. Далее


Общее решение 