Выбираем червячную передачу с двузаходным червяком z 1 = 2. Число зубьев колеса соответственно будет равным:
z 2 = z 1 · iред = 2·16 = 32
Для длительно работающих передач используются червяки с твердостью HRC > 45. В качестве материала червяка применяем закалённую сталь 45. Выбор материала колеса зависит от скорости скольжения, которую оцениваем по формуле [2, c. 24]:
м/с, (19)
где T 2 = P/ w2 = 5000/3,67 = 1362 Н·м – крутящий момент передаваемый колесом.
Исходя из рекомендаций [2, c.25] материалом венца червячного колеса выбираем латунь марки Л66А6Ж3Мц2 со следующими прочностными характеристиками: s в =500 МПа, s т =330 МПа, [s н ]=275–25· vc = 205 МПа.
Определяем коэффициенты долговечности для расчёта передачи по критерию контактной прочности и прочности а изгиб. Коэффициент долговечности для расчёта на контактную прочность равен [2, c 26]:
, (20)
где NHE – число циклов нагружения зубьев колеса за весь срок службы передачи, рассчитываемый по формуле:
, (21)
где ti – срок службы под нагрузкой Ti; c – число зацеплений; m= 4 – показатель степени.
Общий срок службы определяем по выражению:
t S = 365·24· L· · Kсут·Kгод = 365·24·7·0,5·0,6 = 11038 час
где L – число часов в смене; Kсут – коэффициент, учитывающий ежедневное обслуживание передачи и перерывы; Kгод –коэффициент, учитывающий перерывы в работе течении года.
Величины Ti и ti определяем по данным циклограммы нагружения (рис. 2). В результате получим:
NHE = 60·35·(1,394·11038·10-5+(0,65·1038 –11038)·10-5 +
+ 0,84·0,35·11038·105)=18,4·106 c
.
Коэффициент долговечности для расчёта на изгибную прочность равен [2, c 26]:
, (22)
где NFL вычисляется по формуле (21) c m= 9.
В итоге имеем
NFL = 60·35·(1,399·11038·10-5+(0,65·1038 –11038)·10-5 +
+ 0,89·0,35·11038·105)=16,2·106 c;
.
Определяем допускаемое напряжение на изгиб по формуле [2, c.11]:
|
|
[s] F = (0,25s т + 0,08s в) KFL = (0,25·330+0,08·500)·0,73 = 89 МПа.
Допускаемые напряжения при перегрузках
[s] Нпр = 2·s т = 660 МПа; [s] Fпр = 0,8·s т = 264 МПа.
Межосевое расстояние должно удовлетворять условию [2, c.11]:
мм (23)
Выбираем ближайшее стандартное значение межосевого расстояния по ГОСТ 2144-76 равное aw =125 мм.
Модуль червячной пары рассчитываем по выражению
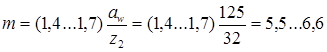мм (24)
Принимаем ближайшее стандартное значение по ГОСТ 2144-76 m= 6,3 мм. Коэффициент диаметра червяка равен:
(25)
Принимаем q= 8. Для правильной работы редуктора необходимо, чтобы было соблюдено условие [2, c. 12]:
q ³ 0,212· z 2 (26)
Условие 8 ³ 0,212·32 = 6,7 – верно.
Определяем коэффициент смещения зуборезного инструмента:
x= (aw / m) – 0,5·(z 2 + q) = 125/6,3 – 20 = –0,16 (27)
На основании полученных предварительных данных производим определение основных геометрических характеристик червячной передачи, необходимых для её последующего конструирования и проверочного расчёта, что представлено в табл. 1.
Таблица 1
Определение основных параметров червячной передачи
| Параметр | Расчётная формула | Расчёт |
| 1. Делительный диаметр червяка | d 1= mq | d 1=6,3·8=50,4 мм |
| 2. Делительный диаметр червячного колеса | d 2= mz 2 | d 2=201,6 мм |
| 3. Начальный диаметр червяка | dw 1= m (q+ 2· x) | dw 1=6,3·(8–2·0,16)=48,4 |
| 4. Диаметр вершин витков червяка | da 1= d 1+2 m | da 1=50,4+12,6=63 мм |
| 5. Диаметр впадин витков червяка | df 1= d 1–2,4 m | df 1=50,4–2,4·6,3=35,3 мм |
| 6. Длина нарезной части червяка | b 1³(11+0,06 z 2) m | b 1³(11+0,06·32)·6,3= = 81,4 мм |
| 7. Угол подъёма витков червяка | g=arctg(z 1/ q) | g=arctg(2/8)=14°09’ |
| 8. Диаметр вершин зубьев колеса | da 2= m (z 2+2+2 x) | da 2= 6,3·(32+2–0,32)= = 212,2 мм |
| 9. Наибольший диаметр колеса | dam 2£ da 2+6 m /(z 1+2) | dam 2£212,2+6·6,3/4= = 221,7 мм |
| 10. Диаметр впадин зубьев колеса | df 2 = m (z 2–2,4+2 x) | df 2 = 6,3·(32–2,4–0,32)= = 184,5 мм |
| 11. Ширина зубчатого венца | b 2 = 0,335 aw | b 2 = 0,335·125=41,9 мм |
|
|
Определяем окружные скорости на червяке и колесе:
v 1 = 0,5·w1· d 1·10–3 = 0,5·58,72·50,4·10–3 = 1,48 м/с; (28)
v 2 = 0,5·w2· d 2·10–3 = 0,5·3,67·201,6·10–3 = 0,34 м/с.
Скорость скольжения:
v 3 = v 1/cosg = 1,48/cos 14°02’ = 1,53 м/с. (29)
Исходя из найденных скоростей назначаем степень точности червячной передачи – 9 [2, c. 28].
Уточняем КПД передачи по формуле:
, (30)
где j' = 3°50’ – приведённый угол трения [1, c. 140].
Находим силы, действующие в зацеплении:
– окружная на колесе, осевая на червяке: 
Н;
– окружная на червяке, осевая на колесе: 
Н;
– радиальные силы: 
Н.
Расчётные контактные напряжения в зацеплении:
МПа (31)
где K =1 – коэффициент нагрузки.
Полученное значение контактных напряжений меньше допускаемого значения, что обеспечит правильную работу редуктора по этому критерию. Для надёжной работы необходимо произвести проверку зубьев на изгиб. Максимальные изгибающие напряжения в зубе рассчитываем по формуле:
МПа,
где YF – коэффициент формы зуба, который определяется по эквивалентному числу зубьев колеса zv 2= z 2/cos3g=35 Þ YF = 1,64 [2, c.28]; x – коэффициент, учитывающий износ зубьев, x=1.
Полученное значение изгибающих напряжений меньше допускаемого, то есть передача требованиям прочности удовлетворяет. Произведём проверку зубьев колеса при кратковременных перегрузках. Соответствующие напряжения будут равны:
МПа < [s] Hпр = 660 МПа;
МПа < [s] Hпр = 264 МПа;
Таким образом, выбранные геометрические параметры червячной передачи удовлетворяют всем условиям прочности.
|
|