Общий проекционный метод для решения линейной системы
Ax = b, (1.1)
Извлекает приближенное решение  из линейного многообразия
из линейного многообразия  размерности m с помощью условия Петрова-Галеркина
размерности m с помощью условия Петрова-Галеркина
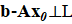 , (1.2)
, (1.2)
где  – еще одно подпространство размерности m. Здесь
– еще одно подпространство размерности m. Здесь  есть произвольное начальное приближение к решению. Метод крыловского подпространства – это метод, в котором в качестве
есть произвольное начальное приближение к решению. Метод крыловского подпространства – это метод, в котором в качестве 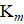 берется крыловское подпространство
берется крыловское подпространство
 (1.3)
(1.3)
где  . Далее используем
. Далее используем  вместо
вместо 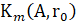 . Разные методы крыловских подпространств соответствуют различным выборам подпространства
. Разные методы крыловских подпространств соответствуют различным выборам подпространства  и разным способам предобуславливания системы.
и разным способам предобуславливания системы.
Хотя все крыловские методы находят полиноминальные приближения одного и того же типа, выбор подпространства  оказывает существенное воздействие на итерационный метод. Два популярных выбора этого подпространства приводят к самым разным методам. Для методов обеих групп имеются блочные обобщения называемые блочными методами крыловского подпространства. Эти методы рассмотрены в [1].
оказывает существенное воздействие на итерационный метод. Два популярных выбора этого подпространства приводят к самым разным методам. Для методов обеих групп имеются блочные обобщения называемые блочными методами крыловского подпространства. Эти методы рассмотрены в [1].
Рассмотрим решение разряженной СЛАУ
Ах = b, (1.4)
где A ∊ 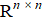 и x, b ∊
и x, b ∊ 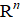 . Итерационные методы часто выбираются для решения таких СЛАУ, и, когда A несимметрична, обычно выбирается алгоритм GMRES. GMRES (от the generalized minimal residual method) – это метод Крыловского подпространства, поэтому он находит приближенное решение
. Итерационные методы часто выбираются для решения таких СЛАУ, и, когда A несимметрична, обычно выбирается алгоритм GMRES. GMRES (от the generalized minimal residual method) – это метод Крыловского подпространства, поэтому он находит приближенное решение 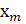 ∈
∈  +
+ 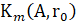 , где
, где  обозначает m -мерное подпространство Крылова,
обозначает m -мерное подпространство Крылова,  – начальная невязка,
– начальная невязка,  –начальное приближение, а
–начальное приближение, а  ≡
≡  . Алгоритм GMRES требует чтобы минимальная невязка системы,
. Алгоритм GMRES требует чтобы минимальная невязка системы,  было минимумом для всех z ∈
было минимумом для всех z ∈ 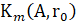 или, что эквивалентно, чтобы невязка после m итераций удовлетворял условию
или, что эквивалентно, чтобы невязка после m итераций удовлетворял условию  .
.
На практике вычислительные ресурсы, требуемые стандартному алгоритму GMRES, могут быть существенными, поскольку требования к памяти и вычислительным ресурсам увеличиваются с каждой итерацией. В этом случае обычно используется перезапущенная версия. В перезапускаемом GMRES (GMRES (m)) параметр перезапуска m обозначает фиксированный максимальный размер для подпространства Крылова. Поэтому, если сходимости не произошло после m итераций, алгоритм перезапускается с  =
=  . Мы называем группу m итераций между последовательными перезапусками циклом. Число перезапуска мы обозначаем нижним индексом:
. Мы называем группу m итераций между последовательными перезапусками циклом. Число перезапуска мы обозначаем нижним индексом:  - невязка после i -циклов или m×i полных итераций. После i циклов невязка представляет собой многочлен в A, умноженный на невязку от предыдущего цикла:
- невязка после i -циклов или m×i полных итераций. После i циклов невязка представляет собой многочлен в A, умноженный на невязку от предыдущего цикла:  =
=  , где
, где  ) – степень m многчлена невязки.
) – степень m многчлена невязки.
Часто возникают случаи, в которых необходимо решить несколько линейных систем с одинаковой матрицей A, но различными правыми частями[8]. Эти линейные системы могут быть записаны как СЛАУ вида:
AX = B, (1.5)
где A ∊ 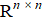 , X, B ∊
, X, B ∊  , а столбцы B - разные правые части. О'Лири впервые представил блочные итерационные методы решения СЛАУ для блочных СЛАУ с симметричной матрицей A с алгоритмом BCG(Block Conjugate Gradient) и других связанных алгоритмов. Для несимметричной матрицы A блочная версия алгоритма GMRES (BGMRES) была впервые описана в [7].
, а столбцы B - разные правые части. О'Лири впервые представил блочные итерационные методы решения СЛАУ для блочных СЛАУ с симметричной матрицей A с алгоритмом BCG(Block Conjugate Gradient) и других связанных алгоритмов. Для несимметричной матрицы A блочная версия алгоритма GMRES (BGMRES) была впервые описана в [7].
BGMRES по существу идентичен стандартному GMRES, за исключением того, что операции выполняются с несколькими, а не с одиночными векторами. Для справки: один цикл перезапуска (i) BGMRES (m) приведен на Алгоритма 1. Итерация Арнольди теперь является процессом ортогонализации блока, создавая основу для блочного метода Крыловского подпространства  , где s обозначает размер блока, а
, где s обозначает размер блока, а 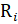 задается в строке 1 на Алгоритме 1. Поскольку линейная система блока (2) имеет s правых частей, подпространство решения теперь имеет размерность m
задается в строке 1 на Алгоритме 1. Поскольку линейная система блока (2) имеет s правых частей, подпространство решения теперь имеет размерность m  s. Как и в случае стандартного алгоритма GMRES, на практике обычно используется перезапущенная версия алгоритма BGMRES (BGMRES (m)).
s. Как и в случае стандартного алгоритма GMRES, на практике обычно используется перезапущенная версия алгоритма BGMRES (BGMRES (m)).
Алгоритм 1. BGMRES (м) для цикла перезапуска i[10].
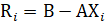

for j = 1: m
 = A
= A 
for i = 1: j
H i,j = 
 =
=  –
– 
end
Uj = 
end
 = [
= [  ,
,  ,...,
,..., 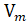 ],
],  =
= 
найти  s.t
s.t 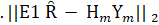 сводящийся к минимуму
сводящийся к минимуму
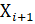 =
=  +
+ 
В дополнение к возможности решения систем с множеством правых частей, BGMRES является эффективным с точки зрения снижения затрат памяти. Решая блочную СЛАУ (в отличие от решения s систем по отдельности), теперь матрица A работает с мультивектором вместо одного вектора на каждой итерации. Поэтому к матрице A обращаются из памяти реже, чем если бы каждая система была решена индивидуально.
Варианты метода Block GMRES были разработаны как для множественных, так и для одиночных систем с правой частью. Для нескольких правосторонних систем гибридный блочный метод GMRES представлен в [3]. Этот блочный метод аналогичен гибридному методу GMRES для систем с одной правой частью, описанному в [7], и часто решает блочную систему быстрее, чем решение систем с одной правой частью, частично из-за меньшего обращения к памяти. Кроме того, в [7] описывается расширение блочного GMRES Моргана с помощью шаблона собственных векторов [9] для нескольких правосторонних систем, а сам Морган разработал расширение блока GMRES-DR (GMRES с принудительным перезапуском) [4]. Такие методы, как методы Моргана, которые дополняют пространство аппроксимации оценками собственных векторов, особенно полезны для умеренно ненормальных матриц с несколькими конкретными собственными значениями (обычно малыми по величине), которые препятствуют сходимости.
Реализация B-LGMRES (m, k) аналогична реализации BGMRES, приведенной в Алгоритме 1. Основное отличие состоит в том, что B-LGMRES находит приближение  при каждом цикле решения одиночных систем с правой частью (1), в отличие от блочной системы (2). Цикл расчета (i) B-LGMRES (m, k) приведен в Алгоритме 2.
при каждом цикле решения одиночных систем с правой частью (1), в отличие от блочной системы (2). Цикл расчета (i) B-LGMRES (m, k) приведен в Алгоритме 2.
Хотя мы говорим о ошибках приближения  ,j=(i−k +1): i как о дополнительных правых векторах, мы решаем только одну правую систему и нам не нужно сохранять приближенные решения блока
,j=(i−k +1): i как о дополнительных правых векторах, мы решаем только одну правую систему и нам не нужно сохранять приближенные решения блока  .
.
Алгоритм 2. B-LGMRES (m, k) для цикла перезапуска i.
 = b − A
= b − A  , β =
, β = 
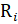 = [
= [  ,
, 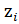 ,...,
,..., 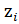 −k+1]
−k+1]
 =
= 
for j = 1:m
 = A
= A 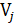
for i = 1:j
 =
= 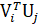
 =
=  –
– 
end
 =
= 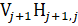
end
 = [
= [ 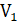 ,
,  ,...,
,...,  ],
],  =
= 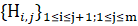
найти  s.t
s.t  сводящийся к минимуму
сводящийся к минимуму
 =
= 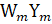
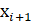 =
=  +
+ 
Вместо этого мы добавляем k последних ошибки приближения к начальной невязке, чтобы сформировать блочную невязку  , как видно в строке 2 Алгоритма 2. Мы нормализуем ошибоку приближения (
, как видно в строке 2 Алгоритма 2. Мы нормализуем ошибоку приближения ( /
/  ), чтобы каждый столбец исходной блочной невязки
), чтобы каждый столбец исходной блочной невязки  был единичной длины. В течение каждого цикла решения генерируется ортогональный базис для блочного Крыловского пространства
был единичной длины. В течение каждого цикла решения генерируется ортогональный базис для блочного Крыловского пространства 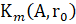 . Oртогональные блочные матрицы размера n×s,
. Oртогональные блочные матрицы размера n×s, 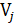 образуют ортогональную матрицу
образуют ортогональную матрицу 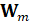 размерности n×m•s, где
размерности n×m•s, где  = [
= [  ,
,  ,...,
,..., 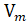 ].
].  представляет собой матрицу Гессенберга размера (m+1)s×m•s с s субдиагоналями, и имеет место следующее стандартное соотношение:
представляет собой матрицу Гессенберга размера (m+1)s×m•s с s субдиагоналями, и имеет место следующее стандартное соотношение:
 , (6)
, (6)
Поскольку B-LGMRES находит минимальную невязку приближенного решения  для A x = b, шаг решения наименьших квадратов (строка 13) отличается от шага стандартного BGMRES (который минимизирует блочную невязку). B-LGMRES находит
для A x = b, шаг решения наименьших квадратов (строка 13) отличается от шага стандартного BGMRES (который минимизирует блочную невязку). B-LGMRES находит  таким образом, что
таким образом, что 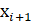 =
=  , где
, где  –размерности m•s×1. В результате треугольную матрицу R из разложения QR в строке 3 не нужно сохранять, так как наименее для решения квадратов требуется только β =
–размерности m•s×1. В результате треугольную матрицу R из разложения QR в строке 3 не нужно сохранять, так как наименее для решения квадратов требуется только β = 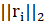 . Как и в случае с BGMRES, B-LGMRES все еще требует применения поворотов
. Как и в случае с BGMRES, B-LGMRES все еще требует применения поворотов  на каждой итерации для преобразования
на каждой итерации для преобразования  в верхнюю треугольную матрицу. Однако теперь на каждом шаге к правой части задачи наименьших квадратов (βe1) необходимо применять только s поворотов.
в верхнюю треугольную матрицу. Однако теперь на каждом шаге к правой части задачи наименьших квадратов (βe1) необходимо применять только s поворотов.