Благодаря локальным этапам минимизации нормы Фробениуса, Bl-BiCGSTAB имеет более плавную сходимость, чем Bl-BCG. Тем не менее, нормы невязки, полученных BlBiCGSTAB, могут колебаться в некоторых случаях. В этом случае мы можем использовать метод блочного сглаживания, чтобы получить нерастущие Фробениусовские нормы невязок.
Для решения линейной системы (1.1) Bl-BiCGSTAB требует для каждой итерации вычисления 2 s матрично-векторных произведений A и общим произведением 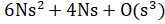 . Это нужно сравнить с s матрично-векторным произведением A, s матрично-векторным произведением
. Это нужно сравнить с s матрично-векторным произведением A, s матрично-векторным произведением 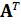 и в общей сложности
и в общей сложности  умножений, необходимых на каждой итерации для Bl-BCG.
умножений, необходимых на каждой итерации для Bl-BCG.
Требования к памяти (исключая требования A, X и B) и основные вычислительные затраты (умножения) на итерацию для алгоритмов Bl-BCG и Bl-BiCGSTAB перечислены в таблице 1.
Таблица 1. – Требования к памяти и вычислительные затраты (умножения) для Bl-BCG и Bl-BiCGSTAB
| Затраты | Bl-BCG | Bl-BCGSTAB |
| Вектор вида A | s | 2 s |
Вектор вида 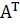
| s | - |
| Умножение | 
| 
|
| Затраты памяти | 
| 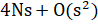
|
Затраты Bl-BCG и Bl-BiCGSTAB быстро увеличивается с увеличением числа правых сторон. Однако эти блочные методы решения сходятся за меньшее число итераций, чем их аналоги по единичного решения правых частей, поскольку размерность пространств поиска увеличиваются на  и
и  и равны s и 2 s соответственно на каждом шаге.
и равны s и 2 s соответственно на каждом шаге.
Как показано в таблице 2, Bl-BiCGSTAB находит решение СЛАУ точнее, чем Bl-GMRES или BiCGSTAB, применяемый для отдельной каждой правой части линейной системы.
Относительная плотность матриц и использование предобуславливания делают блочные методы менее затратными, а потому они более эффективны.
Таблица 2. – Эффективность Bl-BiCGSTAB по сравнению с Bl-GMRES и BiCGSTAB с использованием предобуславливания ILUT
| Matrix | s=5 | s=10 | s=5 | s=10 |
| Utm 1700a (N=1700) (nnz(A)=21313 | 
|  (10)=0.38 (10)=0.38
|  =0.62 =0.62
| 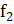 (10)=0.36 (10)=0.36
|
| SAYLR4(N=3564) (nnz(A)=22316) | 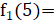 0.77 0.77
|  (10)=0.89 (10)=0.89
|  =0.06 =0.06
| 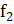 (10)=0.12 (10)=0.12
|
| SHERMAN5(3312) (nnz(A)=20793) | 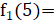 0.93 0.93
|  (10)=0.94 (10)=0.94
|  =0.26 =0.26
| 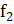 (10)=0.16 (10)=0.16
|
| SHERMAN3(N=5005) (nnz(A)=20033) | 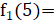 0.82 0.82
|  (10)=1.10 (10)=1.10
|  =0.27 =0.27
| 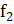 (10)=0.25 (10)=0.25
|
Заключение
Крыловские итерационные блочные методы важны для приложений, в которых возникают линейные системы с многими правыми частями. Однако с теоретической точки зрения они исследованы не слишком хорошо. Помимо их привлекательности при решении линейных систем с несколькими правыми частями, есть и другие аргументы в их пользу: они помогают существенно снизить отрицательный эффект при взятии скалярного произведения при параллельных вычислениях, а также уменьшить количество обменов между разными уровнями памяти при их реализации.
Список использованных источников
1 Саад, Ю. Итерационные методы для разряженных линейных систем / Ю. Саад. – М,: Издательство Московского университета, 2013. – 344 c.
2 Куксенко, С.П. Электромагнитная совместимость: вычислительные методы / С.П. Куксенко – Томск: ТУСУР 2017. – 163 с.
3 Куксенко, С.П. Итерационные методы решения СЛАУ с плотной матрицей / С.П. Куксенко, Т.Р. Газизов. – Томск: ТУСУР, 2007. – 208 с.
4 Jbilou, K. Smoothing iterative block methods for linear systems with multiple right-hand sides / J. Comput, 1999. – P. 97.
5 O’leary, D. The block conjugate gradient algorithm and related methods / D. O’leary, 1980. – P. 293.
6 Fletcher, R. Conjugate gradient methods for indefinite systems / G.A. Watson, R. Fletcher, // In: Proceedings of Dundee Conference on Numerical Analysis – Berlin: Springer-Verlag, 1974.– P. 73.
7 Nillson, M. Iterative Solution of Maxwell's Equations in Frequency BlockQMR_iterative maxwell solution / M. Nillson. Dissertation for the degree of Licentiate of Technology in Numerical Analysis at Uppsala University. 2002. – P. 35-43.
8 Баландин, М.Ю. Методы решения СЛАУ большой размерности / М.Ю. Баландин. Э.П. Шурина. – Новосибирск: НГТУ, 2000 г. – 70с.
9 Guennouni, A. A block version of BICGSTAB for linear systems with multiple right-hand sides / A. El Guennouni, K. Jbilou, H. Sadok. // Electronic Transactions on Numerical Analysis, – 2003 г. – P. 14.
10 Baker, A. H. An efficient block variant of GMRES / A. H. Baker, J.M. Dennis, E. R. Jessup. 2003. –P. 30