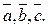Если для множества Е выполняются все вышеперечисленные условия, то множество Е называют линейным пространством.
Нетрудно увидеть, что множество векторов как раз и имеет указанные свойства. Потому элементы линейного пространства Е будем называть векторами: 
А само пространство будем называть векторным.
Пусть заданы n векторов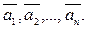 
Заданное множество векторов называют системой векторов. Вектор 
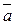называют линейной комбинацией векторов 
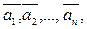если при любых числах 
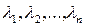имеет место равенство
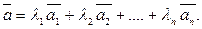
Линейную комбинацию, все коэффициенты которой 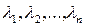равны нулю, принято называть тривиальной. Иначе, линейная комбинация называется нетривиальной.
Система из n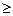 
2 векторов называется линейно зависимой, если существует нетривиальная линейная комбинация этих векторов, равная нулевому вектору, иначе, система векторов называется линейно независимой.
Рангом системы называется максимальное число векторов, образующих линейно независимую систему.
Теорема 1. Система из n 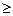2 векторов линейно зависима тогда, когда хотя бы один из векторов является линейной комбинацией остальных.
Теорема 2. Система векторов, содержащая нулевой вектор, линейно зависима.
Теорема 3. Система векторов ранга r, содержащая более r векторов, линейно зависима.
Теорема 4. Система из двух векторов линейно зависима тогда и только тогда, когда эти векторы коллинеарны.
Систему компланарных векторов, среди которых хотя бы два не являются коллинеарными, будем называть системой векторов на плоскости, а систему векторов, среди которых хотя бы одна тройка не является компланарной, - системой векторов в пространстве.
Из рассмотренных выше теорем следует:
1) ранг системы векторов на плоскости равен двум;
2) ранг системы векторов в пространстве равен трем.
Совокупность каких-либо n векторов, взятых из системы векторов ранга n, образующая линейно независимую систему, называется базисом исходной системы векторов.
Учитывая это определение, из ранее рассмотренного следует справедливость следующих утверждений:
1. Любая пара неколлинеарных векторов системы векторов на плоскости может быть взята как базис этой системы, т.е., если 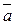и 
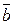- неколлинеарны и взяты как базис этой системы векторов на плоскости, то любой вектор 
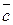этой системы может быть выражен через выбранный базис равенством: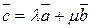 
,
где 
- координаты вектора относительно базиса 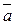и 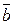, т.е. 
2. Любая тройка некомпланарных векторов системы векторов в пространстве может быть взята как базис этой системы, т.е., если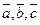 
- некомпланарны и взяты как базис системы векторов в пространстве, то любой вектор 
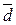этой системы может быть выражен через выбранный базис равенством: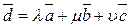 
,
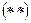где 
- координаты вектора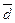 
относительно базиса 
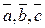, т.е. 
.
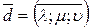Равенства 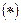и 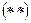называются формулами разложения векторов системы по выбранным базисным векторам.
Выбор базиса дает возможность однозначно поставить в соответствие каждому вектору системы упорядоченный набор чисел – координат вектора в выбранном базисе. И наоборот, каждому упорядоченному набору чисел в некотором базисе однозначно соответствует некоторый вектор.
Замечания: 1. Наиболее рационально выбирать в виде базиса орты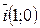 
и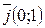 
на плоскости и орты 
в пространстве, т.е., разложение в этих случаях имеет вид:
или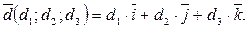 
2. Чтобы проверить линейную независимость векторов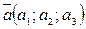 
,
надо составить определитель из координат этих векторов и найти его значение. Если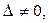 
векторы линейно независимы и образуют базис. Иначе, эти векторы называют компланарными.
3.Чтобы найти координаты вектора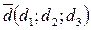 
в данном базисе 
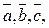т.е., если выполняется равенство 
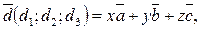необходимо составить систему уравнений относительно переменных x,y,z:
и решить эту систему уравнений любым из известных методов.
Найденные значения переменных x,y,z есть координаты вектора 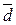в базисе 