Арифметическое суммирование
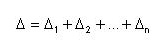а так же используется геометрическое суммирование
Способы суммирования зависят от самих величин, являются ли они скалярными или векторными.
Заметим, что арифметическое суммирование дает завышенный результат (оценку сверху) доверительного интервала суммарной погрешности, поскольку в реальности коэффициенты корреляции могут находиться по модулю в пределах от нуля до единицы.
Суммирование случайных погрешностей с распределениями, отличными от нормального
Для получения доверительного интервала суммарной погрешности, пользуются выражением δΣ= ±kpζΣ, где коэффициент kp определяется из формы закона распределения. Для нахождения закона распределения суммы погрешностей, и, отсюда, коэффициента применяются методы теории вероятностей. Возможны приближенные способы вычисления kp без установления закона распределения суммарной погрешности.
При изготовлении и проведении измерений возникают систематические и случайные погрешности.
Систематическими называют погрешности, постоянные по величине и знаку или изменяющиеся по определенному закону в зависимости от действия определённых заранее предсказуемых причин. Систематические погрешности возникают, например, из-за: неточной настройки оборудования, погрешностей измерительного прибора, отклонения рабочей температуры от нормальной (в т.ч. субъективных действий оператора), силовых деформаций, и др. Систематические погрешности измерения могут быть полностью или частично устранены, например, при помощи поправочной таблицы к неправильно градуированной шкале прибора или путем определения средней арифметической величины из нескольких отсчетов в противолежащих положениях, например, при измерении шага и половины угла профиля резьбы, коррекции неправильных действий оператора (влияние на температуру дыхания или прикосновения, превышение усилий).
Случайными называют переменные по величине и знаку погрешности, которые возникают при изготовлении или измерении и принимают то или иное числовое значение в зависимости от ряда случайно действующих причин. Характерным признаком случайных погрешностей является вариация значений, принимаемых ими в повторных опытах. Эти погрешности вызываются множеством изменяющихся случайным образом факторов таких, как: неточности элементов средства измерения, припуск на обработку, механические свойства материала, сила резания, измерительная сила, различная точность установки деталей на измерительную позицию и другие, причем в общем случае ни один из этих факторов не является доминирующим.
Погрешности изготовления и измерения являются случайными величинами. Примеры случайных величин: размеры деталей при обработке, зазоры в подвижных соединениях, результаты повторных измерений одной и той же величины и т.п.
Если совокупность случайных величин, подчиняется закону нормального распределения или закону близкому к нормальному:
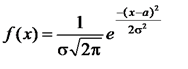где параметр μ — математическое ожидание (среднее значение), медиана и мода распределения, а параметр σ — среднеквадратическое отклонение (σ ² — дисперсия) распределения.
Применяя соответствующие критерии, можно установить, что рассматриваемое эмпирическое распределение наилучшим образом соответствует именно этому закону.
При контроле партии деталей по какому-либо размеру или при многократном измерении одной детали по какому-либо размеру мы встречаемся со случаем, когда результаты наблюдений представляют собой совокупность значений дискретной случайной величины, т. е. совокупность действительных значений размера или значений погрешностей размера.
