В этом случае по данным БИИМ и ПА СНС формируются:
1) скоростные измерения
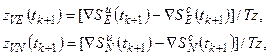(11.35)
где
- приращения декартовых координат объекта в проекциях на географические оси, измеряемые в доплеровском канале современной приемной аппаратуры (ПА) СНС с дискретностью 
;
- приращения декартовых координат, вычисляемые по данным БИИМ о скорости движения объекта;
для предварительной оценки и коррекции погрешностей 
аналога вертикали и
2) позиционные измерения
(11.36)
где
;
, 
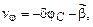
- погрешности СНС по координатам места;
для последующей оценки и коррекции погрешностей 
аналога ИСК (результаты аналогичны режиму начальной выставки ИСОН по данным СНС).
Способ протяженной коррекции БИИМ на конечном интервале времени с использованием алгоритма фильтра Калмана, когда скоростные измерения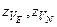 
(например, по данным ГАЛ) используются для демпфирования шулеровских и суточных колебаний погрешностей БИИМ. Позиционное измерение по долготе используется для коррекции координат места. Найдем приближенные аналитические зависимости для дисперсий ошибок оценок 
, характеризующих точность способа протяженной коррекции аналога ИСК в этом случае. Положим, что
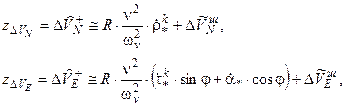(11.37)
или 
(11.38)
где 
- значения оценок погрешностей БИИМ по составляющим вектора линейной скорости, вырабатываемых в фильтре Калмана аналога вертикали после их замыкания в обратной связи (сразу после коррекции аналога вертикали), содержащие прошедшие через демпфируемый шулеровский контур (собственная частота которого 
) БИИМ колебательные составляющие 
погрешностей аналога ИСК с суточной частотой, проекцию 
дрейфов ДУС по оси Мира и ошибки оценки составляющих 
с шулеровской частотой;
- шумы измерений с интенсивностями соответственно 
, характеризуемыми уровнем дисперсий 
согласно решениям (11.19):
(11.39)
Тогда
(11.40)
Аналитическое решение ковариационного уравнения типа Риккати для установившегося режима и оценку времени переходного процесса для рассматриваемой задачи будем искать с использованием раннее рассмотренной процедуры, т.е. перехода от нелинейного матричного уравнения к линейной системе типа (11.27). Собственные значения матрицы 
, т.е. собственные частоты 
ковариационного канала, в данном случае при 
будут равны:
(11.41)
или приближенно при 
(когда 
, что возможно для условий движения МПО в средних широтах) и при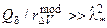 
. (11.42)
Можно показать, что с учетом принятых допущений приближенные аналитические зависимости для дисперсий ошибок оценок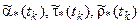 
, характеризующих точность данного способа протяженной коррекции аналога ИСК для средних широт, будут равны:
,
+ 
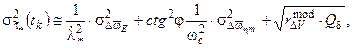
(11.43)
где 
.
Для принятого выше (11.21) уровня инструментальных погрешностей элементов БИИМ и при 
, 
и 
, учитывая также, что погрешности аналога вертикали не превышают 
угл.с, получим, что 
, 
, 
и время переходного процесса в системе практически не отличаются от результатов, полученных при протяженной коррекции по координатам места.