Законы теплового излучения

Между спектральной плотностью энергетической светимости и поглощательной способностью любого тела имеется связь, которая выражается соотношением:

 

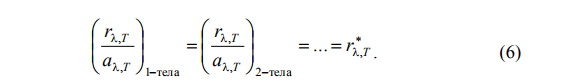
Здесь и далее характеристики, отмеченные звездочкой, относятся к абсолютно черному телу. Соотношение (4.6) называется законом Кирхгофа, а r*_l,T - универсальной функцией Кирхгофа. Этот закон формулируется следующим образом: отношение спектральной плотности энергетической светимости любого тела к его поглощательной способности при данной длине волны и температуре является величиной постоянной для всех тел и равной спектральной плотности энергетической светимости абсолютно черного тела r * _l,T при той же температуре и длине волны (так как a * _l,T = 1).

Из закона Кирхгофа следует, что чем больше тело поглощает, тем больше оно излучает энергии, то есть спектральная плотность энергетической светимости любого тела в любой области спектра всегда меньше спектральной плотности энергетической светимости абсолютно черного тела при тех же значениях l и Т, так как a_l,T < 1.

Зависимость функции от температуры была получена Д.Стефаном (1879 г.) из анализа экспериментальных данных, а затем Л.Больцманом (1884 г.) - теоретическим путем. Эти ученые установили, что энергетическая светимость абсолютно черного тела пропорциональна его абсолютной температуре в четвертой степени:

 

(7)

Где - постоянная Стефана-Больцмана (найденная экспериментально). Формула (7) носит название закона Стефана - Больцмана.

Зависимость длины волны l_max, соответствующей максимуму функции от температуры, устанавливающая смещение l_max в коротковолновый диапазон длин волн при увеличении температуры тела была установлена немецким физиком В.Вином (1893 г.) и получила название закона смещения Вина:

где постоянная Вина.

Закон смещения Вина, таким образом, устанавливает: длина волны, на которую приходится максимум спектральной плотности энергетической свети- мости абсолютно черного тела, обратно пропорциональна абсолютной темпера- туре этого тела. Этот закон объясняет, почему доля энергии, приходящейся на видимые лучи, возрастает, и свечение тела при нагревании переходит от красного к белому калению. Аналитически установить вид функции долгое время не удавалось. Только в 1900 году немецкий физик Макс Планк предположил, что энергия из- лучения испускается телом не непрерывно в виде волн, а отдельными порциями – квантами. Энергия одного кванта:

 

где n - частота излучения, а h = 6,63×10^-34 Дж×с – константа, получившая назва ние постоянной Планка. Исходя из этого предположения, М. Планк получил распределение для спектральной плотности энергетической светимости абсолютно черного тела:

где l - длина волны излучения, c = 3×10⁸ м/с - скорость света в вакууме, k =1,38×10^-23 Дж/К - постоянная Больцмана. Выражение (10) получило название формулы Планка для функции распределения . Из формулы Планка можно получить все законы теплового излучения. Выдвижением гипотезы о дискретности излучения М. Планк заложил основы квантовой теории.

 

1.2. Фотоэффект

Гипотеза Планка о квантах излучения энергии, решившая задачу теплового излучения абсолютно черного тела, получила подтверждение и дальнейшее развитие при изучении явления фотоэлектрического эффекта.

Различают:

1) внешний фотоэффект, при котором облучение светом поверхности приводит к выходу электронов за его пределы;

2) внутренний фотоэффект, при ко- тором происходит увеличение числа свободных электронов внутри вещества;

3) фотогальванический эффект, при котором на границе раздела металла и полупроводника или двух полупроводников при облучении возникает электро- движущая сила;

4) фотоэффект в газовой среде, представляющий собой фо- тоионизацию отдельных молекул или атомов.

Внешний фотоэффект открыл в 1887 году немецкий физик Г. Герц (1857 – 1889), наблюдавший усиление процесса разряда при облучении искрового промежутка ультрафиолетовыми лучами. Первые фундаментальные количественные исследования фо- тоэффекта принадлежат русскому физику А.Г. Столетову (1839 – 1896), который первым перешел к изучению фотоэффекта при низких напряжениях и предложил удобную измерительную схему (рис. 3), употребляемую и до настоящего времени. Полированная металлическая пластинка К, называемая фотокатодом, соединена с отрицательным полюсом батареи.

 

Положительный полюс её через гальванометр соединен с металлической сеткой М, расположенной перед пластинкой. Весь прибор заключался в стеклянный вакуумный сосуд. При освещении пластинки К из нее вырывались электроны, которые летели в сторону металлической сетки М, выполняющей роль анода, в цепи возникал постоянный ток (фототок), который измерялся гальванометром Г. Характер зависимости фототока I от разности потенциалов U между анодом М и катодом К при разных световых потоках Ф (вольт-амперные характеристики) изображен на рис. 4.

 

 

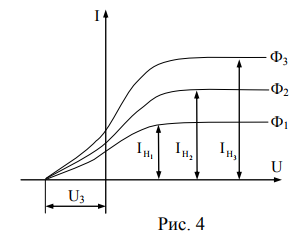
Из рис. 4 видно, что при некотором значении напряжения U фототок достигает максимального значения и далее остается постоянным. Этот ток, называемый «током насыщения», соответствует состоянию, когда все электроны, вырванные светом из фотокатода, достигают анода. При уменьшении напряжения U до нуля фототок уменьшается, но не становится равным нулю, так как вырванные электроны имеют определенную скорость и часть их достигает анода. По цепи будет идти ток. Ток падает до нуля, если приложить к электродам тормозящее поле (U < 0), то есть поменять полярность пластин. При задерживающей разности U₃ фототок обращается в нуль. В этом случае можно утверждать, что все электроны, даже самые быстрые, задерживаются тормозящим полем, и тогда согласно закону сохранения энергии имеем

 

где W_max – максимальная кинетическая энергия фотоэлектронов, m, е, v_max – масса, заряд и максимальная скорость электронов, U₃ – задерживающая разность потенциалов.

Исследования, проведенные А.Г. Столетовым, привели к установлению основных законов внешнего фотоэффекта.

1. Сила фототока насыщения I_н прямо пропорциональна падающему свето- вому потоку Ф:

где – коэффициент пропорциональности, характеризующий чувствительность фотокатода.

2. Скорость фотоэлектронов, вырываемых из тела при фотоэффекте, тем больше, чем больше частота поглощаемого света; начальная кинетическая энергия фотоэлектронов возрастает линейно с возрастанием частоты света.

3. Фотоэффект наблюдается только при облучении светом с частотой критическая, граничная частота фотоэффекта.

4. Фотоэффект практически безынерционен, то есть нет запаздывания между началом освещения и появления фотоэффекта.

 

 

Лишь квантовая теория света позволила успешно объяснить законы внешнего фотоэффекта. Развивая идеи М. Планка о квантовой энергии излучения, А. Эйнштейн высказал гипотезу о том, что свет не только излучается, но и распространяется в пространстве и поглощается веществом в виде отдельных дискретных квантов электромагнитного излучения – фотонов, энергия которых .

По Эйнштейну, в случае поглощения света веществом, каждый поглощенный фотон передает всю свою энергию частице вещества; при внешнем фотоэффекте – электрону. Поэтому число вырванных фотоэлектронов должно быть пропорционально числу поглощенных фотонов, то есть пропорционально интенсивности света (1-й закон фотоэффекта). Безынерционность фотоэффекта объясняется тем, что передача энергии при столкновении фотона с электроном происходит почти мгновенно (4-й закон фотоэффекта). Энергия падающего фотона передается электрону, который расходует эту энергию на работу выхода из металла А и на кинетическую энергию .

На основании закона сохранения энергии

 

Это соотношение называется уравнением Эйнштейна для внешнего фотоэффекта. Уравнение Эйнштейна позволяет объяснить 2-й и 3-й законы фотоэффекта. Из уравнения (1.14) следует, что максимальная кинетическая энергия фотоэлектрона линейно возрастает с увеличением частоты падающего излучения и не зависит от его интенсивности (числа фотонов), так как ни А, ни от интенсивности не зависят (2-й закон фотоэффекта). Максимальная кинетическая энергия обращается в нуль при частоте , соответствующей граничной частоте внеш- него фотоэффекта (3-й закон фотоэффекта):

 

Следовательно, граничная частот зависит только от работы выхода электрона из металла.

Давление света

Свет испускается и поглощается квантами (фотонами), энергия которых равна 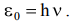. Фотон – элементарная частица, которая всегда движется со скоростью света и не имеет массы покоя. Фотон обладает массой только при движении, и её можно найти из закона взаимосвязи массы и энергии:

где С – скорость света в вакууме.

 

Импульс фотона р_ф равен:

 

где l–длина волны света в вакууме. Из приведенных уравнений следует, что фотон, как и любая частица, характеризуется энергией, массой и импульсом. Формулы (1.9), (1.16) и (1.17) связывают корпускулярные (квантовые) характеристики фотона – массу, импульс и энергию – с волновыми характеристиками света – его частотой ν и длиной волны l.

Пусть монохроматический свет частоты падает на поверхность АВ под углом (рис. 6), а n – число фотонов, падающих за 1 с на единицу площади.

 

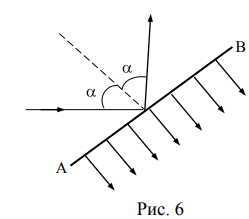
Если r– коэффициент отражения света от рассматриваемой поверхности, то из n фотонов r_n зеркально отражается, а (1-r)n поглощаются. Отражающиеся фотоны передают телу суммарный импульс, направленный нормально к поверхности АВ, равный . Поглощающиеся фотоны передают телу суммарный импульс, равный cos C h n. Таким образом, давление света

 

 

Если n₀ – концентрация фотонов падающего света, и 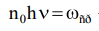– среднее значение объемной плотности энергии света. Тогда

 

Таким образом, давление света одинаково успешно объясняется и волновой, и квантовой теорией.

Эффект Комптона

Наиболее полно и ярко квантовые свойства света проявляются в эффекте Комптона. Явление было изучено в 1923 году американским физиком А. Комптоном (1892 – 1962) и объяснено на основе квантовых представлений о природе света как упругое столкновение γ - фотонов со свободным или слабо связанным электроном в рассеивающем веществе, в результате чего γ- фотон меняет направление распространения и отдает часть энергии электрону, который проявляет себя как «электрон отдачи». К эффекту применимы законы сохранения энергии и импульса, то есть рассеяние, по образному сравнению Комптона, происходит наподобие игры на бильярде фотонами и электронами. Рассеяние монохроматических рентгеновских лучей веществами показывает, что в составе рассеянного излучения наряду с излучением первоначальной l длины волны наблюдается также излучение более длинных волн. Опыты показали, что разность∆l=l^|-l не зависит от длины волны l падающего излучения и природы рассеивающего вещества, а определяется только величиной угла рассеяния

где l_с – комптоновская длина волны (при рассеянии фотона на электроне l_с = 2,246 пм).

Эффект Комптона наблюдается не только на электронах, но и на других заряженных частицах, например протонах, однако ввиду большой массы протона его отдача наблюдается лишь при рассеянии фотонов очень высоких энергий. Рассмотренные явления – изучение абсолютно черного тела, фотоэффект, давление света, эффект Комптона – служат доказательством квантовых (корпускулярных) представлений о свете как о потоке фотонов. С другой стороны, такие явления, как интерференция, дифракция и поляризация, убедительно подтверждают волновую (электромагнитную) природу света. Таким образом, электромагнитное излучение обнаруживает единство, казалось бы, взаимоисключающих свойств – непрерывных (волны) и дискретных (фотоны), которые взаимно дополняют друг друга.

 

Вопросы для повторения

1. Какова особенность теплового излучения, выделяющая его из все известных видов излучения?

2. Каково отличие между черным и серым телами?

3. Каков физический смысл универсальной функции Кирхгофа?

4. Как раз изменится энергетическая светимость черного тела, если его термодинамическая температура увеличится вдвое?

5. Как сместится максимум спектральной плотности энергетической светимости T r, λ черного тела при понижении температуры?