Граф сети Петри. Пример графа сети Петри и описание сети Петри.
В значительной степени теоретическая работа по сетям Петри основана на формальном определении сетей Петри, изложенном выше. Тем не менее, для иллюстрации понятий теории сетей Петри гораздо более удобно графическое представление сети Петри. Теоретико-графовым представлением сети Петри является двудольный ориентированный мультиграф.
Структура сети Петри представляет собой совокупность позиций и переходов. В соответствии с этим граф сети Петри обладает двумя типами узлов. Кружок О является позицией, а планка | — переходом.
Ориентированные дуги (стрелки) соединяют позиции и переходы, при этом некоторые дуги направлены от позиций к переходам, а другие — от переходов к позициям. Дуга, направленная от позиции pi к переходу tj, определяет позицию, которая является входом перехода. Кратные входы в переход указываются кратными дугами из входных позиций в переход. Выходная позиция указывается дугой от перехода к позиции. Кратные выходы также представлены кратными дугами.
Сеть Петри есть мультиграф, так как он допускает существование кратных дуг от од-ной вершины графа к другой. Следует добавить, что так как дуги являются направленными, то это ориентированный мультиграф. Мы знаем, что вершины графа можно разделить на два множества (позиции и переходы) таким образом, что каждая дуга будет направлена от элемента одного множества (позиций или переходов) к элементу другого множества (переходов или позиций); следовательно, такой граф является двудольным ориентированным мультиграфом. В дальнейшем для простоты будем называть его просто графом сети Петри.
Определение 2.3. Граф G сети Петри есть двудольный ориентированный мультиграф,  , где
, где 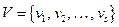 — множество вершин, а
— множество вершин, а  — комплект направленных дуг,
— комплект направленных дуг,  , где
, где  , Множество V может быть разбито на два непересекающихся подмножества
, Множество V может быть разбито на два непересекающихся подмножества  и
и  , таких, что
, таких, что  ,
, 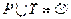 , и для любой направленной дуги
, и для любой направленной дуги  , если
, если  , тогда либо
, тогда либо 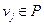 и
и 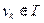 , либо
, либо 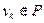 а
а  .
.
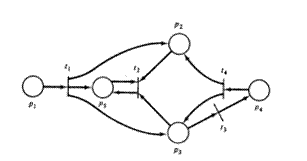
Для примера-1 эквивалентный граф имеет вид:
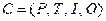
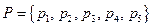
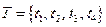
 
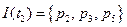 
 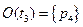
 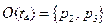
| 
|
Маркировка сети Петри. Формальное определение.
Маркировка  есть присвоение фишек позициям сети Петри. Фишка — это примитивное понятие сетей Петри (подобно позициям и переходам). Фишки присваиваются (можно считать, что они принадлежат) позициям. Количество и положение фишек при выполнении сети Петри могут изменяться. Фишки используются для определения выполнения сети Петри.
есть присвоение фишек позициям сети Петри. Фишка — это примитивное понятие сетей Петри (подобно позициям и переходам). Фишки присваиваются (можно считать, что они принадлежат) позициям. Количество и положение фишек при выполнении сети Петри могут изменяться. Фишки используются для определения выполнения сети Петри.
Определение Маркировка  сети Петри
сети Петри 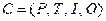 есть функция, отображающая множество позиций
есть функция, отображающая множество позиций  в множество неотрицательных целых чисел
в множество неотрицательных целых чисел  .
.

Маркировка  , может быть также определена как
, может быть также определена как  -вектор
-вектор  , где
, где  и каждое
и каждое  . Вектор
. Вектор  определяет для каждой позиции
определяет для каждой позиции  сети Петри количество фишек в этой позиции. Количество фишек в позиции
сети Петри количество фишек в этой позиции. Количество фишек в позиции  есть
есть 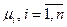 . Связь между определениями маркировки как функции и как вектора очевидным образом устанавливается соотношением
. Связь между определениями маркировки как функции и как вектора очевидным образом устанавливается соотношением  . Обозначение ее в виде функции является несколько более общим и поэтому употребляется гораздо чаще.
. Обозначение ее в виде функции является несколько более общим и поэтому употребляется гораздо чаще.
Маркированная сеть Петри 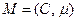 есть совокупность структуры сети Петри
есть совокупность структуры сети Петри 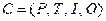 и маркировки
и маркировки  и может быть записана в виде
и может быть записана в виде  .
.
На графе сети Петри фишки изображаются маленькой точкой в кружке, который представляет позицию сети Петри. На рис. 2.11 и 2.12 приведены примеры графического представления маркированной сети Петри.
ПРИМЕР 1 из предыдущей лекции
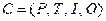
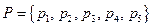
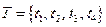
 
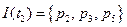 
 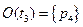
 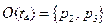
| 
|


Так как количество фишек, которое может быть определено для каждой позиции, неограниченно, то в целом для сети Петри существует бесконечно много маркировок. Множество всех маркировок сети Петри, обладающей  позициями, есть множество всех
позициями, есть множество всех  -векторов,
-векторов,  . Это множество, хотя и бесконечно, является счетным.
. Это множество, хотя и бесконечно, является счетным.