Состояние сети Петри определяется ее маркировкой. Запуск перехода изменяет состояние сети Петри посредством изменения маркировки сети. Пространство состояний сети Петри, обладающей 
позициями, есть множество всех маркировок, т. е. 
.
Изменение в состоянии, вызванное запуском перехода, определяется функцией изменения 
, которую мы назовем функцией следующего состояния. Когда эта функция применяется к маркировке 
(состоянию) и переходу 
,она образует новую маркировку (состояние), которая получается при запуске перехода в маркировке . Так как может быть запущен только в том случае, когда он разрешен, то функция 
не определена, если не разрешен в маркировке . Если же разрешен, то 
, где 
есть маркировка, полученная в результате удаления фишек из входов и добавления фишек в выходы .
Определение Функция следующего состояния 
для сети Петри 
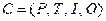с маркировкой и переходом 
определена тогда и только тогда, когда 
для всех 
. Если определена, то 
, где 
для всех 
. Пусть дана сеть Петри 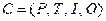с начальной маркировкой 
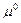. Эта сеть может быть выполнена последовательными запусками переходов. Запуск разрешенного перехода в начальной маркировке образует новую маркировку 
. В этой новой маркировке можно запустить любой другой разрешенный переход, например 
образующий новую маркировку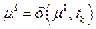 
. Этот процесс будет продолжаться до тех пор, пока в маркировке будет существовать хотя бы один разрешенный переход. Если же получена маркировка, в которой ни один переход не разрешен, то никакой переход не может быть запущен, функция следующего состояния не определена для всех переходов, и выполнение сети должно быть закончено.
Множество достижимости сети Петри. Сети Петри для моделирования. Примитивные и непримитивные события. Понятие конфликта.
Пусть некоторый переход в маркировке разрешен и, следовательно, может быть запущен. Результат запуска перехода в маркировке есть новая маркировка 
. Говорят, что является непосредственно достижимой из маркировки , иными словами, состояние непосредственно получается из состояния .
Определение 2.9. Для сети Петри 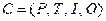с маркировкой маркировка называется непосредственно достижимой из , если существует переход 
, такой, что
Можно распространить это понятие на определение множества Достижимых маркировок данной маркированной сети Петри. Если непосредственно достижима из , a 
— из , говорят, что достижима из .
Определим множество достижимости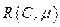 
сети Петри 
с маркировкой как множество всех маркировок, достижимых из . Маркировка принадлежит 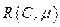, если существует какая-либо последовательность запусков переходов, изменяющих на .
Отношение «достижимости» является рефлексивным, транзитивным замыканием отношения «непосредственной достижимости».
Определение 2.10. Множество достижимости 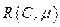для сети Петри 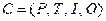с маркировкой есть наименьшее множество маркировок, определенных следующим образом:
1. 
;
2. Если 
и 
для некоторого , то 
.