Входная информация для самоконтроля.
Приступая к изучению данной темы, Вам необходимо восстановить в памяти (или восполнить) знания:
- из предыдущих разделов:определение предела функции в точке, теоремы о пределах, односторонние пределы (ПМ - МА. 5).
Содержание темы
Структурно-логическая схема содержания темы
 |
9.2.2. Тематическое содержание.
Непрерывность функции в точке и на промежутке. Основные определения.
Понятие непрерывности функции является одним из основных понятий математического анализа. Непрерывные функции обладают целым рядом важных свойств, которых лишены функции разрывные. Эти свойства создают большие удобства при использовании непрерывных функций в различного рода исследованиях, имеющих огромное теоретическое и практическое значение.
Определение 1 непрерывности функции в точке (9.1).
Функция y = f (х), определенная в окрестности точки х 0, называется непрерывной в точке х 0, если она определена в этой точке, существует  и этот предел равен значению функции в точке х 0, то есть
и этот предел равен значению функции в точке х 0, то есть 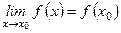 .
.
9.1. Определение 1 непрерывности функции в точке (адрес файла Блок 4 ___).
Функция y = f (х), определенная в окрестности точки х 0, называется непрерывной в точке х 0, если она определена в этой точке, существует  и этот предел равен значению функции в точке х 0, то есть и этот предел равен значению функции в точке х 0, то есть 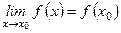 .
Вернитесь к тексту .
Вернитесь к тексту
|
Заметим, что равенство 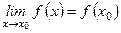 , определяющее понятие непрерывности функции в точке можно представить в виде
, определяющее понятие непрерывности функции в точке можно представить в виде
 ,
,
так как  . А словами можно сказать так: функция f (х) непрерывна в точке х 0, если предел функции в этой точке равен значению функции от предела аргумента, то есть возможен предельный переход под знаком функции. То есть, если f (х) непрерывна и нужно вычислить ее предел при х ® х 0, то достаточно в выражение функции вместо х подставить х 0 и подсчитать соответствующее значение f (х 0). Это и будет искомой предел.
. А словами можно сказать так: функция f (х) непрерывна в точке х 0, если предел функции в этой точке равен значению функции от предела аргумента, то есть возможен предельный переход под знаком функции. То есть, если f (х) непрерывна и нужно вычислить ее предел при х ® х 0, то достаточно в выражение функции вместо х подставить х 0 и подсчитать соответствующее значение f (х 0). Это и будет искомой предел.
Приращение функции и приращение аргумента.
Пусть задана функция y = f (х)определенная на некотором интервале. При этом: х 0 – внутренняя точка этого интервала, х – любое другое значение независимой переменной из этого же интервала.
Приращение аргумента (9.2).
Приращением аргумента называется разность х – х 0 и обозначается через D х, то есть D х = х – х 0.
| 9.2. Приращение аргумента (адрес файла Блок 4 ____). Приращением аргумента называется разность х – х 0 и обозначается через D х, то есть D х = х – х 0. Вернитесь к тексту |
Иначе говоря, D х – величина, которую нужно прибавить к первоначальному значению аргумента х 0, чтобы получить х.

| х – х 0 = D х х = х 0 + D х |
Приращение функции (9.3).
Приращение функции в точке х 0, вызванным приращением аргумента D х, называется разность f (х 0 + D х) – f (х 0) и обозначается через D f или D у.
| 9.3. Приращение функции (адрес файла Блок 4 ___). Приращение функции в точке х 0, вызванным приращением аргумента D х, называется разность f (х 0 + D х) – f (х 0) и обозначается через D f или D у. Вернитесь к тексту |
f (х 0) – называется начальным значением функции
f (х 0 + D х) – наращенным значением функции.
Приращение функции дает величину, на которую изменяется значение функции при переходе от первоначального значения х 0 аргумента к наращенному значению х 0 + D х.

Определение 2 непрерывности функции в точке (9.4).
Функция f (х) называется непрерывной в точке х 0, если бесконечно малому приращению аргумента в этой точке соответствует бесконечно малое приращение функции, то есть
 .
.
9.4. Определение 2 непрерывности функции в точке (адрес файла Блок 4 ___).
Функция f (х) называется непрерывной в точке х 0, если бесконечно малому приращению аргумента в этой точке соответствует бесконечно малое приращение функции, то есть
 .
Вернитесь к тексту .
Вернитесь к тексту
|
Пользуясь выражением для D f = D у, можно записать также, что
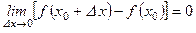 ,
,
или, иначе
 .
.
Но так как х 0 + D х = х, то х при D х ® 0 будет стремится к х 0 и последнее равенство можно переписать так:
 ,
,
что совпадает с определением 1 непрерывности функции.
Пример 1. Доказать, что функция y = sin x непрерывна в точке х 0 = 1.
Решение. Для доказательства дадим х 0 = 1 приращение D х, х = х 0 + D х = 1 + D х. Приращение функции D у определим из соотношения
D у = f (х 0 + D х) – f (х 0) = f (1 + D х) – f (1) = sin (1 + D х) – sin 1 =
 .
.
Найдем
 .
.
Следовательно, функция y = sin x в точке х 0 = 1 непрерывна, т.к.  .
.
В разделе ВМ. МА – 5 мы познакомились с понятием односторонних пределов: левосторонний и правосторонний пределы.
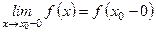 – левосторонний предел
– левосторонний предел
 – правосторонний предел.
– правосторонний предел.
Определение 3 непрерывности функции в точке (9.5).
Функция f (х) называется непрерывной в точке х 0, если существуют односторонние пределы, они равны между собой и равны значению функции в точке х 0, то есть
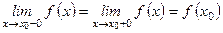 .
.
9.5. Определение 3 непрерывности функции в точке (адрес файла Блок 4 ___).
Функция f (х) называется непрерывной в точке х 0, если существуют односторонние пределы, они равны между собой и равны значению функции в точке х 0, то есть
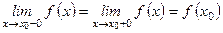 .
Вернитесь к тексту .
Вернитесь к тексту
|
Определение непрерывной функции на промежутке (9.6).
Функция f (х) называется непрерывной на некотором промежутке, если она непрерывна в каждой точке этого промежутка.
| 9.6. Определение непрерывной функции на промежутке (адрес файла Блок 4 ___). Функция f (х) называется непрерывной на некотором промежутке, если она непрерывна в каждой точке этого промежутка. Вернитесь к тексту |