Определения: числового ряда, n-ой частичной суммы, суммы числового ряда. Определение сходящегося и расходящегося ряда.
Числовым рядом называется выражение, имеющее вид:
Где числа 
, 
– члены ряда, образующие числовую последовательность, а 
– общий член ряда.
Сумма первых n членов числового ряда называется n-ой частичной суммой ряда.
Суммой числового ряда называют предел последовательности его частичных сумм при неограниченном увеличении номера частичных сумм.
Числовой ряд называют сходящимся, если он имеет сумму, и расходящимся, если сумма отсутствует.
Необходимый признак сходимости ряда. Пример сходящегося и расходящегося ряда.
Ряд сходится при условии, стремления к нулю общего члена ряда при неограниченном увеличении его номера.
Сходящийся ряд:
Расходящийся ряд:
Достаточные признаки сходимости знакоположительных рядов.
Обычный и предельный признаки сравнения, признак Даламбера, радикальный и интегральный признаки Коши.
Определение знакочередующегося ряда. Признак Лейбница.
Ряд называется знакочередующимся, если его члены попеременно то положительны, то отрицательны.
Если абсолютные величины членов знакочередующегося ряда убывают, и предел его общего члена при неограниченном возрастании n равен нулю, то ряд сходится, а его сумма не превосходит первого члена.
Абсолютная и условная сходимость.
Знакопеременный ряд называют абсолютно сходящимся, если сходится ряд, состоящий из абсолютных значений членов данного ряда. Если же данный ряд сходится по Лейбницу, но ряд из абсолютных величин его членов расходится, то исходный ряд называют условно сходящимся.
Определение функционального ряда. Область сходимости ряда.
Функциональным называется ряд, члены которого – непрерывные функции от x. При конкретном значении x функциональный ряд становится числовым, который либо сходится, либо расходится.
Совокупность значений аргумента, при которых функциональный ряд сходится, называется областью сходимости ряда.
Определение степенного ряда. Теорема Абеля.
Функциональный ряд вида 
,
где 
, – действительные числа, называется степенным рядом.
Если степенной ряд сходится при 
, то он сходится для всех 
.
Если степенной ряд расходится при 
, то он расходится для всех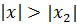 
.
Определение ряда Тейлора, Маклорена (найти разложение любой элементарной функции в ряд Маклорена по определению). Способы разложения функций в степенные ряды.
Если функция в некотором интервале раскладывается в степенной ряд по степеням (
) то разложение задается формулой Тейлора:
Если 
, то имеем дело с разложением Маклорена (разложением Тейлора по степеням 
):
Разложение производится путем вычисления коэффициентов через значения производных по формуле или с использованием рядов элементарных функций.
9. Ряд Фурье для периодической с периодом 2l функции, заданной на интервале [-l;l].
Если функция задана на интервале 
, где 
– произвольное число, имеет период 
и удовлетворяет условиям теоремы Дирихле, то данная функция может быть представлена в виде суммы ряда Фурье:
Коэффициенты находятся по формулам:
, 
, 
.