Практическая работа № 9
Тема: МАТЕРИАЛЬНЫЕ РАСЧЕТЫМОЛОЧНОЙ ПРОМЫШЛЕННОСТИ
Цель: изучить основные способы материальных расчетов в молочной промышленности, знать порядок расчета степени использования составных частей молока при его переработке; потери сырья на производство.
Теоретические сведения
Основные уравнения
Общий материальный баланс может быть подан уравнением, левую часть которого составляет масса всех видов сырья и материалов, которые поступают на переработку, –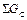 
а правая часть – это масса полученных продуктов 
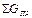но производственные потери 
:
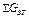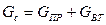. (1)
Производственные потери выражают в процентах от количества переделанного сырья:
.
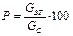Отсюда:
,
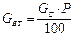и уравнение (1) приобретает вид:
, (2)
где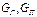 
– масса готового и побочного продуктов соответственно, кг; (их сумма составляет 
);
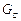– масса сырья, кг;
Р – потери сырья %.
Для отдельных производств молочной промышленности уравнение (2) имеет такой вид:
сепарация: 
;
производство сыра: 
;
производство масла: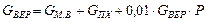 
;
производство сухого молока: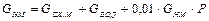 
_
где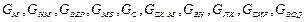 
– соответственно масса молока, нормализованного молока, сливок, масла, сыра, сухого молока, обезжиренного молока, пахты, сыворотки, воды, кг.
Уравнение по компонентного баланса (баланс составных частей молока):
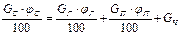, (3)
где 
– содержание составляющих молока в сырье %;
– содержание составляющих молока в готовом продукте %;
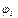– содержание составляющих молока в побочном продукте %;
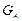– потери составные молока, кг.
Потери составных частей молока выражают в процентах от соответствующих составляющих:
откуда 
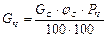, (4)
где 
– потери составные молока %.
После подстановки (4) в (3) получаем:
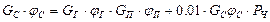. (5)
Уравнение (5) может быть записано за будь – какой частью молока – за жиром Же, сухим остатком молока С, сухим обезжиренным молочным остатком (СЗМЗ) О.
|
|
Во время ориентировочных расчетов производственными потерями пренебрегают.
Пример 1. Сколько сливок жирностью 30 % можно получить при сепарации 500 кг молока жирностью 4 %? Потери жира при сепарации 0,36 %, содержание жира в обезжиренном молоке 0,05 %.
Решение:
Развязать предложенный пример можно алгебраизмом или графическим методом (за расчетным треугольником или квадратом).
Метод алгебраизма. Составим уравнение общего и покомпонентного балансов:
,
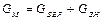Определим из первого уравнения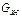 
и подставим его в уравнение покомпонентного баланса:
или
.
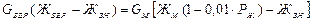Отсюда
Графический метод. При расчете массы нормализующих компонентов в практике пользуются графическими методами – треугольником и квадратом.
При расчете по треугольнику в его вершинах записывают массовую долю жира компонентов, входящих в уравнение материального баланса. Например, при нормализации обезжиренным молоком, в вершинах треугольника записывают – Жм, Жнм, Жом; при нормализации сливками – Жм, Жнм, Жсл, для процесса сепарирования молока – Жм, Жсл, Жом.
На внешних сторонах треугольника указывают разности между большим и меньшим содержанием жира, на внутренних сторонах треугольника массу компонентов напротив соответствующих значений массовой доли жира на вершинах треугольника. Тогда на каждой стороне треугольника получаем соотношения, из которых выводим расчетные формулы.
Например, Жнм<Жм, тогда Мнм=Мм+Мом. Заполняем треугольник следующим образом. Из треугольника составляем пропорцию с соответствии с правилом расчетного треугольника: отношение внутренних сторон к внешним – величина постоянная. Для полученного треугольника:
|
|
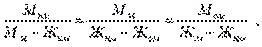
Если Мм известна, то объединяя члены пропорции попарно, вводим расчетные формулы для Мом и Мнм.
При расчете по квадрату Пирсона в центре его записывают желаемую жирность смеси двух компонентов: Жнм - при нормализации молока, Жм – при сепарировании молока.
По углам квадрата с левой стороны – жирность компонентов: Жм и Жом, Жм и Жсл – при нормализации молока, Жм и Жом – при сепарировании молока. В углах с правой стороны квадрата показывают разности по диогоналям между большей и меньшей величинами. Это разницы показывают количество отношений между компонентами смеси: Мм и Мом, Мм и М сл – для нормализации молока, М сл и Мом – для сепарирования молока. Например, Жнм<Жм; Мнм=Мм+Мом. Квадрат имеет вид:
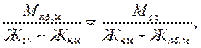
Если известна масса смеси и необходимо определить массу ее компонентов, то суммируют полученные разности в правой части квадрата, например: Жсл-Жнм+Жнм-Жом=Жсл-Жоб.м
Полученные величины показывают количественное соотношение между цельным и обезжиренным молоком. Найденные и написанные по углам квадрата справа разности суммируют и находят относительное количество смеси (нормализованного молока). Разности и их сумма говорят о том, что на (Жсл-Жо) часте нормализованного
Для определения количества сливок с учетом потерь необходимо полученный результат умножить на коэффициент потерь:
Количество сливок с учетом производственных потерь:
|
|
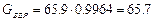кг.
Пример 2 В приемный цех завода поступило 42400 кг молока жирностью 3,8 % и сливок 9600 кг жирностью 30,5 %. Норма потерь сырья и жира при принятии молока и сливок составляет 0,05 %. Определить фактические потери, экономию (перерасходы) молока и сливок при принятии, если в отделение для хранения из приемного цеха передано 42387 кг молока и 9596 кг сливок.
Решение
1. Определим количество жира в сырье, которое поступило в приемный цех:
кг.
2. Определим количество жира в сырье, которое передали в отделение для хранения:
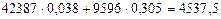кг.
3. Фактические потери жира составляют:
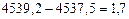кг
или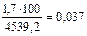 
% от жира в сырье, которое поступило в приемный цех.
4. Определим потери жира за нормой:
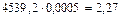кг.
5. Следовательно, экономия сравнительно с утвержденными предельно допустимыми потерями жира составляет:
кг
или в пересчете на молоко:
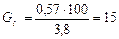кг.
Степень использования составных частей молока при его переработке
Степень перехода – это частица составных частей молока, что перешла к готовому продукту, от количества составных частей молока в переделанном сырье:
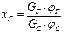, (6)
где 
– степень перехода составных частей молока, од.
Выразив количество продукта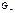 
из-за количества потраченного сырья:
,
где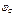 
– содержание составляющих молока в сырье %;
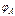– содержание составляющих молока в готовом продукте %;
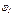– содержание составляющих молока в побочном продукте %
Подставив его в предыдущую формулу, получим:
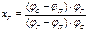, (7.)
или в процентах:
.
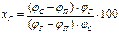Степень использования составных частей молока определяют по фактическим данным или с учетом производственных потерь фактических, или предельно допустимых. Он меньше от степени перехода составных частей молока в готовый продукт:
или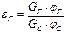 
_
где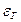 
– степень использования % (од.);
– масса фактически потраченного сырья, кг;
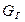– масса фактически полученного готового продукта, кг.
Виразивши массу готового продукта через массу сырья с учетом потерь:
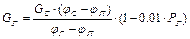
И подставив в (8), одержимо:
, (9)
где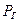 
– фактические или предельно допустимые потери составных частей молока (%) от их количества, которое было в переделанном молоке.
При многостадийной переработке сырья показатели степени перехода и степени использования составных частей молока равняются произведениям степени перехода или произведениям степени использования за стадиями переработки:
;
,
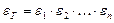где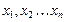 
– степени перехода составляющих молока на стадиях его переработки;
– степени использования составные молока на стадиях переработки.
Пример 3. Из 6200 кг молока жирностью 3,3 % выработано 1000 кг сливок жирностью 20 %. Содержание жира в обезжиренном молоке 0,05 %. Определить степень перехода жира в сливки при сепарации и степень использования жира при производстве сливок.
Решение:
1. Определим степень перехода жира в сливки при сепарации за формулой (6):
%.
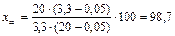2. Определим степень использования жира при производстве сливок за формулой (7):
%.
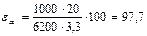