Внутренние силы. Метод сечений

Модели формы.

Конструкции имеют в большинстве случаев сложную форму, отдельные элементы которой можно свести к основным типам: стержень, оболочка, массив.

Модели нагружения.

Силы являются мерой механического взаимодействия элементов конструкций. Силы бывают внешние и внутренние. Внешние, объемные.

Модели разрушения.

Моделям нагружения соответствуют модели разрушения – уравнения (условия), связывающие параметры работоспособности элемента конструкции в момент разрушения с параметрами, обеспечивающими прочность.

Внутренние силы. Метод сечений

Взаимодействие между частями (частицами) внутри элемента конструкции характеризуется внутренними силами.

Внутренние силы представляют собой силы межатомного взаимодействия (связей), возникающие при воздействии на тело внешних нагрузок.

Практика показывает, что внутренние силы определяют прочностную надежность детали (тела).

Для нахождения внутренних сил используют метод сечений. Для этого мысленно рассекают тело на две части, одну часть отбрасывают, другую рассматривают совместно с внешними силами. Внутренние силы распределены по сечению некоторым сложным образом. Поэтому систему внутренних сил приводят к центру тяжести сечения, чтобы можно было определить главный вектор и главный момент М внутренних сил, действующих по сечению. Затем раскладываем главный вектор и главный момент на составляющие по трем осям и получаем внутренние силовые факторы сечения: составляющая N_z называется нормальной, или продольной си­лой в сечении, силы Q_x и Q_y называются поперечными силами, момент M_z (или M_к) называется крутящим моментом, а моменты M_х и M_y - изгибающими моментами относительно осей х и y, соответственно.

Таким образом, если внешние силы заданы, то внутренние силовые факторы вычисляются как алгебраические суммы проекций сил и моментов, действующих на мысленно отсеченную часть тела.

После определения числовых значений внутренних сил строят эпюры – графики (диаграммы), показывающие как изменяются внутренние силы при переходе от сечения к сечению.

4. напряжении и диформации в точке

5.общие принципы расчета элементов конструкции: Модели прочностной надежности элементов конструкций: модели конструкционного материала; модели геометрической формы; модели нагружения; модель предельного состояния разрушения. Дать определение характеристик материала: упругость, пластичность, ползучесть, хрупкость, твердость.

Критерии работоспособности деталей машин: прочность, жесткость, устойчивость, и др.

Внутренние силы. Определение внутренних сил. Метод сечений

Напряжение как основная характеристика внутренних сил. Напряжения в точке сечения.

Механические характеристики материалов. Рассмотреть механические свойства пластических и хрупких материалов при сжатии. Сформулировать условия прочности на растяжение и сжатие для пластических и хрупких материалов. Коэффициент запаса прочности, факторы, влияющие на выбор коэффициента запаса прочности.

Деформации. Продольная и поперечная деформации при растяжении (сжатии). Закон Гука.

6. внутренние силы, напряжения и деформации при растяжении и сжатии:

7. закон гука при растяжении и сжатии: Закон Гука при растяжении и сжатии справедлив лишь в определенных пределах нагружения и формулируется так: нормальное напряжение прямо пропорционально относительному удлинению или укорочению. Математически закон Гука можно записать в виде равенства:

σ = Еε.

Коэффициент пропорциональности Е характеризует жест­кость материала, т. е. его способность сопротивляться упругим деформациям растяжения или сжатия, и называется модулем продольной упругости или модулем упругости первого рода.Модуль упругости и напряжение выражаются в одинаковых единицах:

[Е] = [σ]/[ε] = Па.

8. механические свойства конструкционных материалов: Основным механическим свойствам конструкционных материалов и сплавов, определяющим работоспособность конструкции и область их применения, относят: твердость, прочность, упругость, пластичность, вязкость, выносливость.

 

Твердость – сопротивление материала проникновению в него индентора, из другого более твердого материала.

Прочность – способность материала сопротивляться разрушению при воздействии внешних напряжений. Определяем усилие разрушения.

Упругость – способность материала восстанавливать свои размеры и форму при снятии внешних напряжений.

Пластичность – способность материала изменять форму и размеры при воздействии усилия.

Вязкость - это сопротивление материала динамическому, ударному воздействию нагрузки. В этом случае мы определяем работу разрушения.

9. методы оценки прочности элементов конструкции:

Оценка прочности конструкции выполняется по результатам сопоставления действительного состояния конструкции с предельным состоянием. Существуют два основных метода оценки прочности: расчет по допускаемым напряжениям и расчет по предельному состоянию (предельным нагрузкам). Методы отличаются критериями для определения предельного состояния.При расчете по допускаемым напряжениям в качестве предельного принимается состояние, при котором хотя бы в одной точке элемента конструкции расчетное напряжение становиться равным предельному значению. По этому методу расчет выполняется с использованием условия прочности

Данный метод является основным и используется в большинстве случаев.Однако для конструкций, изготовленных из пластичных материалов, более целесообразным является расчет по предельному состоянию. В этом случае в качестве предельного принимается состояние, при котором происходит исчерпание несущей способности конструкции. Это означает, что при постоянной нагрузке начинается неограниченный рост деформаций. При этом методе расчета условие прочности имеет вид

где F – действующая нагрузка; [ F ] – допускаемая нагрузка.

10. внутренние силовые факторы и деформации при сдвиге: Кроме деформаций растяжения. сжатия или изгиба материал может испытывать деформацию сдвига. Как показано в разделе 2.1 (см. таблицу 2.1), при воздействии внешних нагрузок в поперечных сечениях бруса возникают поперечные силы Q_x и Q_y.

Считается, что деформация сдвига (среза) возникает при действии двух равных противонаправленных сил, лежащих в плоскостях соседних поперечных сечений бруса. Параллельные сечения сдвигаются друг относительно друга на угол g с осью. При этом касательные напряжения в плоскости поперечного сечения равномерно распределены по его поверхности площадью А, так что равны

, (2.9)

где Q = F - внутренняя поперечные сила, равная соответствующей внешняя поперечной нагрузка F.

На рис.2.10 показано, что под действием горизонтальных сил F может произойти срез заклепок по плоскости нахлестки соединяемых листов, так что площадь поверхности среза заклепки равна площади поперечного сечения ее стержня .

11. Закон Гука при сдвиге: Установлено: касательные напряжения пропорциональны углу сдвига в определенных пределах упругой деформации сдвига. Соотношение - формула закона Гука при сдвиге.Коэффициент пропорциональности G в формуле закона Гука при сдвиге - модуль сдвига. Модуль сдвига измеряется в МПа, кН/см2, кгс/см2, кгс/мм2. Угол сдвига –безразмерная величина.Модуль сдвига (G) – это физическая постоянная для материала, характеризующая жесткость при сдвиге. Значение модуля сдвига (G) может быть определено экспериментально.

12. расчеты на прочность при сдвиге: Условие прочности детали конструкции заключается в том, что наибольшее напряжение, возникающее в ней (рабочее напряжение), не должно превышать допускаемое.
Расчетная формула при сдвиге:

τ = Q / А ≤ [τ]

читается следующим образом: касательное напряжение при сдвиге не должно превышать допускаемое. (при обозначении предельно допустимых напряжений применяют квадратные скобки: [τ] или [σ])
По этой расчетной формуле проводят проектный и проверочный расчеты и определяют допускаемую нагрузку.

Деформация сдвига, доведенная до разрушения материала, называется срезом (применительно к металлам) или скалыванием (применительно к неметаллам).
Допускаемое напряжение на срез выбирают для пластичных материалов в зависимости от предела текучести.
В машиностроении для штифтов, болтов, шпонок и других деталей, работающих на срез принимают [τ_ср] = (0,25….0,35) σ_т, где σ_т– предел текучести материала изделия.

При расчетах на срез в случае, если соединение осуществляется несколькими одинаковыми деталями (болтами, заклепками и т. д.), полагают, что все они нагружены одинаково. Расчеты соединений на срез обычно сопровождают проверкой прочности этих соединений на смятие.

13. геометрические характеристики плоских сечений: - статические моменты площади сечения ()

- осевые моменты инерции ()

- центробежный момент инерции ()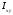

- полярный момент инерции ()

- моменты сопротивления ()

- радиусы инерции ().

Рассмотрим поперечное сечение бруса в системе координат х0у.

Выделим элементарную площадку dA координатами х и у.

На основании теоремы Вариньона (из курса теоретической механики):

Где - координаты центра тяжести фигуры.

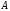- площадь фигуры.

14. внутренние силовые факторы при кручении: Кручением называется нагружение, при котором в поперечном сечении бруса возникает только один внутренний силовой фактор — крутящий момент.

Внешними нагрузками также являются две противоположно на­правленные пары сил.

Рассмотрим внутренние силовые факторы при кручении круг­лого бруса (рис. 26.1). Для этого рассечем брус плоскостью I и рассмотрим равновесие отсеченной части (рис. 26.1а). Сечение рассматриваем со стороны отброшенной части.

Внешний момент пары сил разворачивает участок бруса про­тив часовой стрелки, внутренние силы упругости сопротивляются повороту. В каждой точке сечения возникает поперечная сила dQ (рис. 26.1б). Каждая точка сечения имеет симметричную, где возни­кает поперечная сила, направленная в обратную сторону. Эти силы образуют пару с моментом

dm = pdQ;

р — расстояние от точки до центра сечения. Сумма поперечных сил в сечении равна нулю:

С помощью интегрирования получим суммарный момент сил упругости, называемый крутящим моментом:

Практически крутящий момент определяется из условия равно­весия отсеченной части бруса.

Крутящий момент в сечении равен сумме моментов внешних сил, действующих на отсеченную часть (рис. 26.1 в):

 

 

15. деформации и напряжения при скручивании:

16. геометрические характеристики при кручении:

17.

18. опоры и опорные реакции:

Шарнирно-подвижная

Шарнирно-неподвижная

Заделка (жесткое защемление стержня)

Шарнир – соединение элементов позволяющее свободно поворачиваться этим элементам.

В опорных частях возникает сила противодействия внешним усилиям (нагрузки).

Силы противодействия в опорных частях внешней нагрузки получили название опорные реакции или опорные силы, или реактивные силы. Стержни на 2 опорах называют балками.

Опорная реакция – мера противодействия внешним силам в местах опирания системы (в опорных частях конструкции).

Определение опорных реакций в статических определяемых системах.

Статически определяемая система (конструкция) – это такая система, в которой все усилия могут быть определены из условий статического равновесия.

19. внутренние силовые факторы при изгибе стержня: