F=0.26x1+0.28x2+0.3x3+0.29x4=min

F=0.26x1+0.28x2+0.3x3+0.29x4+0x5+0x6+0x7+0x8+0x9+M(y1+y2+y3+y4)=min

| C0 | P0 | B | 0.26 | 0.28 | 0.3 | 0.29 | M | M | M | M | ∑ | β | |||||
| X1 | X2 | X3 | X4 | X5 | X6 | X7 | X8 | X9 | Y1 | Y2 | Y3 | Y4 | |||||
| X5 | |||||||||||||||||
| M | Y1 | -1 | |||||||||||||||
| M | Y2 | -1 | |||||||||||||||
| M | Y3 | -1 | |||||||||||||||
| M | Y4 | -1 | |||||||||||||||
| 1530M | 4M-0.28 | 8M-0.28 | 4M-0.3 | 4M-0.29 | -M | -M | -M | -M | |||||||||
| X5 | 2/3 | 2/3 | 1/3 | 1/3 | -1/3 | 218/3 | 70/3 | ||||||||||
| 0.28 | X2 | 1/3 | 1/3 | 2/3 | -1/3 | 1/3 | 547/3 | - | |||||||||
| M | Y2 | 5/3 | -1/3 | 4/3 | 1/3 | -1 | -1/3 | 68/3 | 20/3 | ||||||||
| M | Y3 | -2/3 | 7/3 | -4/3 | 2/3 | -1 | -2/3 | 121/3 | 80/3 | ||||||||
| M | Y4 | 1/3 | -2/3 | -4/3 | 2/3 | -1 | -2/3 | 85/3 | 60/3 | ||||||||
| 50.4+90M | 4/3M-1/6 | 4/3M-31/150 | -4/3M-31/300 | 5/3M-7/75 | -M | -M | -M | -8/3M+7/75 |
Дальнейшее решение было проведено на компьютере и получены следующие ответы: всего подлежит раскрою 200 плит, причем все раскраиваются вторым способом, тогда мы получим 600 заготовок первого вида, 200 – второго, 400 – третьего, 400 – четвёртого, при минимальных отходах, равных 56 м2.
Экономическая сущность и математическое моделирование транспортных задач.
Известны: пункты производства (А1, А2 … Ai … Аm); m – пунктов, производящих конкретную продукцию;
аi – мощность i-поставщика (сколько необходимо реализовать продукции, т. е. перевести из Аi)
 – суммарная мощность поставщиков в плановом периоде;
– суммарная мощность поставщиков в плановом периоде;
пункты потребления (В1, В2 … Bj … Вn); n – пунктов потребления конкретной продукции;
bj – потребность (спрос, ёмкость) j-поставщика в конкретной продукции;
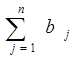 – суммарный спрос n-потребителей.
– суммарный спрос n-потребителей.
1)  – сбалансированные спрос и предложение, такие задачи называются закрытыми транспортными задачами;
– сбалансированные спрос и предложение, такие задачи называются закрытыми транспортными задачами;
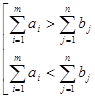 – открытая транспортная задача.
– открытая транспортная задача.
2) возможна поставка продукции из любого пункта производства в любой пункт потребления.
3) сij – затраты на поставку продукции, т. е. критерий оптимальности (может быть и на производство, и на транспортировку).
В задаче требуется найти план транспортных связей между поставщиками и потребителями продукции, при котором потребности всех потребителей были бы удовлетворены с минимальными суммарными затратами на поставку всей продукции.
xij – объём поставки от i-поставщика к j-потребителю (искомая величина)
| Поставщики и их мощности | Потребители и их спрос | ||||||
| B1 ………………………….. Bj ………………………………….. Bn | |||||||
| b1 …………………………… bj ………………………………….. bn | |||||||
| С=[ сij] mxn / Х=[ xij]mxn | |||||||
| A1 | a1 | c11 | ……………………. x11………………… | c1j | …………………. ………x1j……… | c1n | ……………… ………….. x1n |
| . . . | . . . | . . . | ... ... ... | . . . | ... ... ... | . . . | ... ... ... |
| Ai | ai | ci1 | ……………………. xi1………………… | cij | …………………. ………xij……… | cin | ……………… ………….. xin |
| . . . | . . . | . . . | . . . | . . . | |||
| Am | am | cm1 | ……………………. xm1………………… | c11 | …………………. ………xmj……… | c11 | ……………… …………..xmn |
Целевая функция:
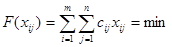 (1)
(1)
Условие реализации продукции у каждого из поставщиков:
 (2)
(2)
Условие обеспечения всех потребителей продукцией по их потребности:
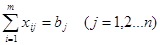 (3)
(3)
Условие не отрицательности переменных:

В решении системы линейных уравнений 2 и 3 необходимо найти такие не отрицательные значения переменных, чтобы целевая функция принимала минимальное значение.
m+n-1 – линейно независимых уравнений, ранг системы, r= m+n-1.
В каждом опорном плане должно быть m+n-1 базисных элементов (xij>0), если таких переменных равно или больше, чем m+n-1, план называется невырожденный; если одна или несколько базисных переменных равна нулю, то такой план считается вырожденным.
Открытые транспортные задачи.
a) 
 (1)
(1)
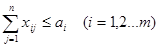 (2)
(2)
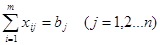 (3)
(3)

Bn+1:  – потребность какого-то потребителя, находящегося за пределами района (фиктивный потребитель).
– потребность какого-то потребителя, находящегося за пределами района (фиктивный потребитель).
 (1)
(1)
 (2)
(2)
 (3)
(3)


сi, n+1=0 (i=1,2…m)
б) 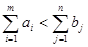
 (1)
(1)
 (2)
(2)
 (3)
(3)

Аn+1: 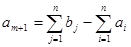 – фиктивный поставщик.
– фиктивный поставщик.
 (1)
(1)
 (2)
(2)
 (3)
(3)


Ограничение транспортных возможностей.
а) xij=0 => cij=М, где М»0;
б) 0 ≤ хij ≤ dij
dij – характеризует транспортные возможности между i-поставщиком и j-потребителем.
Тогда поставщик Аi условно делится на Аi` и Аi``, при этом ai`=dij и ai``= ai`-dij, cij`=cij и cij``=М, где М»0.