Задача квадратичного программирования

Всем требованиям, позволяющим корректно записать необхо­димые и достаточные условия для седловой точки (Х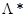^*; ) функ­ции Лагранжа в виде выражений (6), удовлетворяет задача квадратичного программирования.

Определение 8. Квадратичной формой относительно переменных х₁,x₂, …,x_n называется числовая функция от этих переменных, имеющая вид

(7)

Определение 9. Квадратичная форма F называется положительно определенной, если F (Х) > 0 для всех значений переменных Х = ( х₁,x₂, …,x_n ), кроме Х = 0.

Определение 10. Квадратичная форма F называется отрицательно определенной, если F (Х) < 0 для всех значений переменных Х = ( х₁,x₂, …,x_n ), кроме Х = 0.

Определение 11. Квадратичная форма F называется положительно -полуопределенной, если F (Х) ≥ 0 для любого набора значений переменных Х =(х₁,х₂,..., х_n) и, кроме того, существует такой набор переменных Х' = ( х’₁,x’₂, …,x’_n ), где не все значения переменных одновременно равны нулю, что F (Х') = 0.

Определение 12. Квадратичная форма F называется отрицательно -полуопределенной, если F (Х) ≤ 0 для любого набора значений переменных Х =(х₁,х₂,..., х_n) и, кроме того, существует такой набор переменных Х' = ( х’₁,x’₂, …,x’_n ), где не все значения переменных одновременно равны нулю, что F (Х') =0.

Теорема 3. Квадратичная форма является выпуклой функ­цией, если она положительно-полуопределенная, и вогнутой функцией, если она отрицательно-полуопределенная.

Определение 13. Задача, состоящая в определении максимального (минимального) значения функции

(8)

при ограничениях

(9)

где - отрицательно (положительно) -полуопределен­ная квадратичная форма, называется задачей квадратичного программирования.

Для задачи квадратичного программирования функция Лагранжа запишется в виде

(10)

Если функция L имеет седловую точку

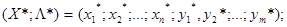
то в этой точке выполняются условия Куна - Таккера.

Вводя дополнительные переменные

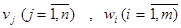(11)

обращающие неравенства (8) в равенства, перепишем выражения (8), записанные для задачи квадратичного программирования, следующим образом:

Таким образом, чтобы получить решение задачи квадратичного программирования (10) - (12), необходимо определить неотрицатель­ное решение систем линейных уравнений (15) и (16), удовлетворяющее условиям (17), (18), (19).

Это решение может быть получено с помощью метода искусственного базиса. Используя метод искусственного базиса, дополнительно учитывая условия (17), (18), после конечного числа шагов либо установим неразрешимость, либо получим оптимальный план ис­ходной задачи.

Итак, методика получения решения задачи квадратичного программирования (10) - (12) включает следующие этапы.

1. Составить функцию Лагранжа.

2. Записать в виде выражений (15) - (19) необходимые и достаточные условия существования седловой точки функ­ции Лагранжа.

3. Используя метод искусственного базиса, либо установить отсутствие седловой точки для функции Лагранжа, либо вычислить ее координаты.

4. Записать оптимальное решение исходной задачи и вычислить значение целевой функции.