Пример решения задачи квадратичного программирования

Задача 2. Вычислить максимальное значение функции

, (20)

 

при условиях , (21)

Решение.

1. Анализ условий задачии обоснование выбора метода решения.

Функция Fявляется вогнутой, так как представ­ляет собой сумму двух функций: 1) линейной функции

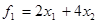, (22)

которая (как любая другая линейная функция) является одновременно вогнутой и выпуклой и

2) квадратичной формы

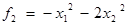, (23)

которая является отрицательно-определенной и, следовательно, также вогнутой.

Система ограничений задачи включает только линейные неравенства.

Целевая функция является дифференцируемой во всем диапазоне изменения переменных х₁ и х₂.

Следовательно, такая задача может быть решена методом множителей Лагранжа с применением теоремы Куна- Таккера.

Составим функцию Лагранжа

(24)

и запишем необходимые и доста­точные условия существования ее седловой:

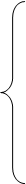
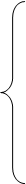
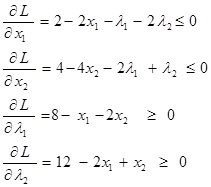(25)

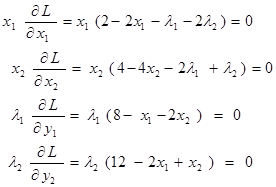(26)

 

Систему линейных неравенств (25) перепишем следующим образом:

 

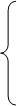
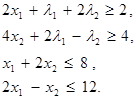(27)

 

Переходя к канонической форме задачи, введем дополнительные неотрицательные перемен­ные v₁, v₂, w₁, w₂ обращающие неравенства (27) в равенства, получим

 

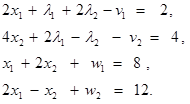(28)

 

x₁,x₂, λ₁, λ_2, v₁,v₂,w₁,w₂ ≥ 0

 

Учитывая ограничения (17), (18), запишем:

 

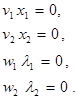(29)

 

Если теперь получить базисное решение системы линейных урав­нений (28) с учетом выполнения равенств (29), то будет получена седловая точка функции Лагранжа для исходной задачи, т. е. определено оптимальное решение.

Для получения базисного решения системы линейных урав­нений (28) воспользуемся методом искусственного базиса.

В пер­вое и второе уравнения системы (28) (уравнения, полученные из частных производных по переменным х₁ и х₂, т.е. не по λ₁ и λ₂), соответственно добавим искусственные неотрицательные переменные z₁, и z₂ и рассмот­рим задачу линейного программирования, состоящую в определении максимального значения функции

 

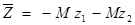(30)

 

при условиях

 

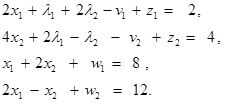(31)

 

x₁,x₂, λ₁, λ_2, v₁,v₂,w₁,w_2, z₁, z₂ ≥ 0. (32)

 

В результате решения задачи (30)-(32) (отметим, что при этом решении учитываются условия (17,18) получим допустимое базисное решение системы линейных уравнений (31) (таблица 1 – объединенная таблица).

 

Запишем задачу (30-32) в векторной форме.

 

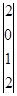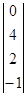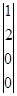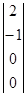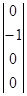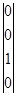Рх₁ = Рх₂ = Р_λ1 = Р_λ2 = Р_υ1 = Р_υ2 = Р_W1 = Р_W2 =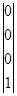

 

Р_Z1 = 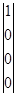Р_Z2 = Р₀ =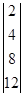

 

На первом шаге имеем единичный ортогональный базис, состоящий из векторов P_Z1, P_Z2, . Р_W1, Р_W2.

 

Таблица 13.1 – Поиск базисного решения

i

Базис

СБ

Р0

-М

-М

Px1

Px2

Pλ1

Pλ2

Pv1

Pv2

Pw1

Pw2

PZ1

PZ2

PZ1

-М

-1

PZ2

-М

-1

-1

Pw1

Pw2

-1

-6

-2

-4

-3

-1

Pz1

-М

-1

Px2

1/2

-1/4

-1/4

Pw1

-1

½

½

Pw2

½

-1/4

-1/4

-2

-1

-2

-1/2

Px1

1/2

-1/2

Px2

1/2

-1/4

-1/4

Pw1

-3/2

-1/2

1/2

-1/4

Pw2

-1/2

-5/4

-1/4

 

x₁^* = 1; x₂^* = 1; w₁ = 5; w₂ = 11; λ₁^* = λ₂^* = v₁ = v₂ = 0.

 

Так как x₁^*v₁ = 0; x₂^*v₂ = 0 =0; λ₁^*w₁ = 0; λ₂^*w² = 0; то точка

(X*; 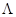*) = (1;1;0;0) является седловой точкой функции Лагранжа для исходной задачи.

Следовательно, Х* = (1; 1) - оптимальный план исход­ной задачи и

F _max = 2x₁ + 4x₂ - x₁² - 2x₂² = 2 1 + 4 1 – 1 – 2 = 3.

 

* * *

2. Практическая часть (индивидуальные задания). Решить задачу аналитическим методом

Вариант 1. Вычислить максимальное значение функции

F = x₁ + 4x₂ + x₁x₂ – 2x₁² – 2x₂²

при условиях: х₁ + 2х₂ ≤ 12,

3х₁ + х₂ ≤ 15.

х₁, х₂ ≥ 0

Вариант 2. Вычислить максимальное значение функции

F = -x₁² - x₂² + x₁ + 8x₂

при условиях: х₁ + х₂ ≤ 7,

х₂ ≤ 5.

х₁, х₂ ≥ 0

Вариант 3. Вычислить максимальное значение функции

F = -2x₁ + 8x₂ + x₁x₂ – x₁² –x₂²

при условиях: х₁ + 2х₂ ≤ 12,

-х₁ + х₂ ≥ - 8.

х₁, х₂ ≥ 0

Вариант 4. Вычислить максимальное значение функции

F = -x₁² - x₂² - 2x₃² + 2x₂ + 3х₃

при условиях: х₁ + х₂ + х3 ≤ 18,

х₂ ≤ 12.

х₁ + 2х₃ ≤ 14

х₁, х_2, х₃ ≥ 0

Вариант 5. Вычислить максимальное значение функции

F = 2x₁ + 4x₂ + x₁x₂ – 2x₁² – 3x₂²

при условиях: х₁ + 2х₂ ≤ 13,

3х₁ + х₂ ≤ 19.

х₁, х₂ ≥ 0

Вариант 6. Вычислить максимальное значение функции

F = -3x₁² - x₂² + x₁ + 6x₂

при условиях: х₁ + х₂ ≤ 9,

х₂ ≤ 8.

х₁, х₂ ≥ 0

Вариант 7. Вычислить максимальное значение функции

F = -4x₁ + 8x₂ + x₁x₂ – 2x₁² –x₂²

при условиях: х₁ + 2х₂ ≤ 12,

-х₁ + х₂ ≥ - 8.

х₁, х₂ ≥ 0

Вариант 8. Вычислить максимальное значение функции

F = -3x₁² - x₂² - 2x₃² + 3x₂ + 3х₃

при условиях: х₁ + х₂ + х3 ≤ 17,

х₂ ≤ 14.

х₁ + 2х₃ ≤ 15

х₁, х_2, х₃ ≥ 0

Вариант 9. Вычислить максимальное значение функции

F = 5x₁ + 4x₂ + x₁x₂ – 4x₁² – 6x₂²

при условиях: х₁ + 2х₂ ≤ 13,

3х₁ + х₂ ≤ 19.

х₁, х₂ ≥ 0

Вариант 10. Вычислить максимальное значение функции

F = -5x₁² - x₂² +3 x₁ + 8x₂

при условиях: х₁ + х₂ ≤ 10,

х₂ ≤ 15.

х₁, х₂ ≥ 0

Вариант 11. Вычислить максимальное значение функции

F = -4x₁ + 8x₂ + x₁x₂ –3 x₁² –2x₂²

при условиях: х₁ + 2х₂ ≤ 16,

-х₁ + х₂ ≥ - 9.

х₁, х₂ ≥ 0

Вариант 12. Вычислить максимальное значение функции

F = -3x₁² - x₂² - 4x₃² + 2x₂ + 8х₃

при условиях: х₁ + х₂ + х3 ≤ 20,

х₂ ≤ 14.

х₁ + 2х₃ ≤ 16

х₁, х_2, х₃ ≥ 0

Вариант 13. Вычислить максимальное значение функции

F = 6x₁ + 4x₂ + x₁x₂ – 3x₁² – 5x₂²

при условиях: х₁ + 2х₂ ≤ 17,

3х₁ + х₂ ≤ 19.

х₁, х₂ ≥ 0

Вариант 14. Вычислить максимальное значение функции

F = -4x₁² - 2x₂² + x₁ + 4x₂

при условиях: х₁ + х₂ ≤ 8,

х₂ ≤ 15.

х₁, х₂ ≥ 0

Вариант 15. Вычислить максимальное значение функции

F = -3x₁ + 8x₂ + x₁x₂ – 3x₁² –7x₂²

при условиях: х₁ + 2х₂ ≤ 21,

-х₁ + х₂ ≥ - 4.

х₁, х₂ ≥ 0

Вариант 16. Вычислить максимальное значение функции

F = -6x₁² - x₂² - 2x₃² + 3x₂ + 3х₃

при условиях: х₁ + х₂ + х₃ ≤ 11,

х₂ ≤ 13.

х₁ + 2х₃ ≤ 17

х₁, х_2, х₃ ≥ 0

Вариант 17. Вычислить максимальное значение функции

F =4x₁ + 4x₂ + x₁x₂ – 4x₁² – 3x₂²

при условиях: х₁ + 2х₂ ≤ 17,

3х₁ + х₂ ≤ 19.

х₁, х₂ ≥ 0

Вариант 18. Вычислить максимальное значение функции

F = -7x₁² - x₂² + 4x₁ + 2x₂

при условиях: х₁ + х₂ ≤ 17,

х₂ ≤ 15.

х₁, х₂ ≥ 0

Вариант 19. Вычислить максимальное значение функции

F = -9x₁ + 8x₂ + 2x₁x₂ –3 x₁² –2x₂²

при условиях: х₁ + 2х₂ ≤ 21,

-х₁ + х₂ ≥ - 4.

х₁, х₂ ≥ 0

Вариант 20. Вычислить максимальное значение функции

F = -3x₁² - x₂² - 3x₃² + 4x₂ + х₃

при условиях: х₁ + х₂ +2 х₃ ≤ 16,

х₂ ≤ 14.

х₁ + 2х₃ ≤ 12

х₁, х_2, х₃ ≥ 0

Вариант 21. Вычислить максимальное значение функции

F = 4x₁ + 4x₂ + 3x₁x₂ – 4x₁² – 5x₂²

при условиях: х₁ + 2х₂ ≤ 22,

3х₁ + х₂ ≤ 18.

х₁, х₂ ≥ 0

 

Вариант 22. Вычислить максимальное значение функции

F = -5x₁² - 3x₂² + 2x₁ + 4x₂

при условиях: х₁ + х₂ ≤ 17,

х₂ ≤ 25.

х₁, х₂ ≥ 0

Вариант 23. Вычислить максимальное значение функции

F = -6x₁ + 8x₂ + x₁x₂ –4 x₁² –6 x₂²

при условиях: х₁ + 2х₂ ≤ 11,

-х₁ + х₂ ≥ - 3.

х₁, х₂ ≥ 0

Вариант 24. Вычислить максимальное значение функции

F = -8x₁² - x₂² - 4x₃² + 6x₂ + 3х₃

при условиях: х₁ + х₂ + х3 ≤ 23,

х₂ ≤ 22

х₁ + 2х₃ ≤ 17

х₁, х_2, х₃ ≥ 0

Вопросы для самоконтроля

1. Сформулируйте вербально теорему Куна – Таккера

2. Запишите условия оптимальности решения задачи выпуклого программирования с применением теоремы Куна-Таккера

3. Что собой представляет седловая точка функции Лагранжа? В чем заключается особенность этой точки?

4. Какие условия должны быть выполнены, для того чтобы можно было применять теорему Куна-Таккера?

5. Запишите постановку задачи квадратичного программирования в общем виде

6. Каковы особенности задачи квадратичного программирования?

7. Запишите условия Куна –Таккера для задачи квадратичного программирования.

8. В чем заключается доказательство того, что данная задача относится к задаче квадратичного программирования?

Основная литература:

1.Методы оптимальных решений в экономике и финансах: учебник; под ред. В.М. Гончаренко, В.Ю. Попова.-М.: КНОРУС, 2013.-400с.

2. Исследование операций в экономике: Учеб. пособие для вузов/Под ред. проф. Н.Ш. Кремера.- М.: ЮНИТИ, 2010, 411 с.

Дополнительная литература

1. Акулич И.Л. Математическое программирование в примерах и задачах: Учеб. пособие для студентов эконом. спец. вузов.- м.:Высш.шк., 1986.- 319 с.

2. Смирнов В.Е. Учебно-методическое пособие для подготовки и проведения практического занятия 6 по дисциплине Методы оптимальных решений., РГГУ, филиал в г. Домодедово, электронное издание, 2019. – 18 с.

 

Отчет должен содержать:

1. Титульный лист (тема и цель занятия)

2. Индивидуальные исходные данные

3. Выполнение индивидуального задания

4. Экономическую интерпретацию полученных результатов

5. Ответы на контрольные вопросы (в письменной форме)

 

* * *