Пример решения задачи выпуклого программирования с ограничениями - неравенствами

Среда 2 пара – Э31 – МОР ПЗ 6

УЧЕБНО-МЕТОДИЧЕСКОЕ ПОСОБИЕ

Для подготовки и проведения практического занятия 6 по дисциплине

МЕТОДЫОПТИМАЛЬНЫХ РЕШЕНИЙ

(направление ЭКОНОМИКА)

Тема: Выработка и принятие оптимальных решений в задачах выпуклого нелинейного программирования с ограничениями неравенствами

Разработал профессор СМИРНОВ В.Е.

Теоретическая часть

В задачах нелинейного программирования ограничения могут принимать выражения - равенства и неравенства.

Существуют два вида постановки задач нелинейного программирования с ограничениями неравенствами:

- общая задача нелинейного программирования

F(х₁,х₂,..,х_n) → max (min) (целевая функция);

g_i(х₁,х₂,..,х_n) =; ≥; ≤ b_i, i = 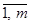; (функциональные ограничения)

x₁,x₂,…,x_n ≥ 0; (прямое ограничение)

- стандартная задача нелинейного программирования:

- стандартная задача нелинейного программирования максимизации:

F(х₁,х₂,..,х_n) → max (целевая функция);

g_i(х₁,х₂,..,х_n) ≤ b_i, i = 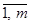; (функциональные ограничения)

x₁,x₂,…,x_n ≥ 0;

- стандартная задача нелинейного программирования минимизации:

F(х₁,х₂,..,х_n) → min (целевая функция);

g_i(х₁,х₂,..,х_n) ≥ b_i, i = 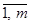; (функциональные ограничения)

x₁,x₂,…,x_n ≥ 0; (прямое ограничение)

- стандартная задача смешанного нелинейного программирования:

F(х₁,х₂,..,х_n) → max (целевая функция);

g_i(х₁,х₂,..,х_n) ≤ b_i, i = ; (функциональные ограничения)

g_i(х₁,х₂,..,х_n) = b_k, k = ; (функциональные ограничения)

x₁,x₂,…,x_n ≥ 0; (прямое ограничение);

Для того, чтобы перейти от задачи на минимум к задаче на максимум необходимо:

- целевую функцию умножить на (-1);

- функции ограничения вида g_i(х₁,х₂,..,х_n) ≥ b_i также умножить на (-1), при этом получим функцию ограничения вида (- g_i(х₁,х₂,..,х_n) ≤ - b_i).

От смешанной задачи также можно перейти к задаче на максимум. Для этого необходимо произвести следующие тождественные преобразования. Функцию ограничение вида g_i(х₁,х₂,..,х_n) = b_k заменить на две функции ограничения: g_i(х₁,х₂,..,х_n) ≤ b_i,

- g_i(х₁,х₂,..,х_n) ≤ - b_i.

Однако отметим, что такое преобразование в отдельных случаях может оказаться некорректным.

- вместо стандартной задачи на максимум иногда применяют унифицированный вид этой задачи, где все ограничения имеют стандартный вид функции, т.е. прямые ограничения х₁,х₂,…,х_n должны быть преобразованы к виду (-x) ≤ 0. Тогда обозначив g_{m + i}(х₁,х₂,..,х_n) = - x_i и положив b_m+i = 0 это неравенство можно записать в виде

g_{m + i}(х₁,х₂,..,х_n) = b_{m + i}.

Таким образом, унифицированный вид задачи на максимум запишется в виде:

F(х₁,х₂,..,х_n) → max (целевая функция);

g_i(х₁,х₂,..,х_n) ≤ b_i, i = 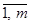; (функциональные ограничения),

g_{m + n}(х₁,х₂,..,х_n) = b_{m + n} (прямые ограничения).

Определение 1. Ограничение g_i(х₁,х₂,..,х_n) ≤ b_i, i = 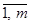; будем называть активным в точке х*, если g_i(х₁*,х₂*,..,х_n*) = b_i. В противном случае – неактивным.

Если ограничение равенство, т.е. уравнение, то решение задачи следует искать на пересечении поверхностей, описываемых функцией цели и функциями ограничений. Такие задачи решаются методом неопределенных множителей Лагранжа.

Если ограничение – неравенство, то для решения задачи нелинейного программирования в особых условиях можно использовать метод множителей Лагранжа с применением теоремы Куна – Таккера.

Такими особыми условиями в первую очередь выступают условия выпуклости (вогнутости) целевой функции и функций ограничений, а также условие регулярности множества допустимых решений по Слейтеру.

Множество точек называется выпуклым, если оно вместе с любыми своими двумя точками содержит и весь отрезок, соединяющий эти точки.

Если [a,b] - отрезок на числовой прямой и , то x = α a + (1 – α) b, где 0 ≤ α ≤ 1 или x = α₁ a + α₂ b, α₁ + α₂ = 1, α₁ ≥ 0, α₂ ≥ 0. (1)

Из этого утверждения следует и обратное: если выполняется (1), то .

Таким образом, отрезок [a,b] можно определить как множество всех точек х, удовлетворяющих условию (1).

Тогда, выпуклое множество – это множество, которое вместе с любой парой своих точек (a,b) содержит и все точки х, для которых выполняется (1) (рис.1).

Исходя из равенства (1), используя метод индукции, можно показать, что если М – выпуклое пространство, то для любых точек и любых действительных чисел t_i ≥ 0, удовлетворяющих условию .

х2

х2

х1

х1

 

 

а) выпуклое множество а) невыпуклое множество

 

Рисунок 1 – Пояснения к понятию выпуклости множеств

Эти определения отрезка и выпуклого множества сохраняются для случая, когда a,b, …, x – точки n – мерного пространства (тогда операции в равенстве (1) выполняются покоординатно)).

Определение 2. Функция f (x₁,x₂,…,x_n ), заданная на выпуклом множестве Х, называется выпуклой (рис.2), если для любых двух точек Х₁ и Х₂ из допустимого множества Х и любого 0 ≤ λ ≤ 1 выполняется соотно­шение

. (2)

Определение 3. Если в неравенстве (2) заменить знак ≤ на знак ≥, то функция будет вогнутой, т.е. функция является вогнутой, если выполняется условие (рис.2) 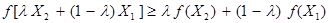. (3)

		х1			х1

а) выпуклая б) вогнутая

 

Рисунок 2 – Пояснения к выпуклости и вогнутости функций

Иногда выпуклые и вогнутые функции называют соответственно выпуклыми вниз и выпуклыми вверх. Отсюда следует определение.

Определение 4. Задача нелинейного программирования называется зада­чей выпуклого nрограммирования, если целевая функция F (x₁,x₂,…,x_n ), является вогнутой или выпуклой, а функции ограничений g_i (Х) (i= 1, т)­ выпуклыми.

Теорема. 1. Любой локальный максимум (минимум) задачи выпуклого nрограммирования является глобальным максимумом (минимумом).

Следствием этой теоремы является следующее. Экстремум любой функции одной переменной, как правило, доказывают с помощью условия Якоби. Вместе с тем, условие Якоби носит локальный характер, т.е. его выполнение зависит от анализируемой точки экстремума, что не всегда приемлемо. Выпуклые же функции обладают свойством, позволяющим от локального условия Якоби перейти к глобальному (не зависящему от рассматриваемой точки. Это условие называется условием Слейтера.

Определение 5. В стандартной з адаче нелинейного программирования на максимум условие Слейтера выполняется в том случае, если существует, по крайней мере, одна такая допустимая точка х* = (х₁*,х₂*,….х_n*) X, в которой все функциональные ограничения выполняются как строгие неравенства т. е.

g_i(х₁,х₂,..,х_n) < b_i, i = .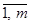

Наряду с общим существует и модифицированное условие Слейтера, которое требует выполнение строго неравенства только для нелинейных функций (если функция линейная, то выполнение условия Слейтера для нее не обязательно).

Определение 6. Функцией Лагранжа задачи выпук­лого нелинейного программирования является функция

(4)

где λ₁, λ₂, …, λ_m- множители Лагранжа, т.е. функция аналогичная функции Лагранжа для задач нелинейного программирования с ограничениями равенствами.

Однако классический метод множителей Лагранжа не применим, если ограничения в задаче нелинейного программирования представляют собой неравенства.

Одним из путей решения такой задачи является использование теоремы Куна –Таккера. Эта теорема занимает центральное место в теории нелинейного программирования.

Необходимые и достаточные условия существования экстремума нелинейной функции в заданных ограничениях Куна –Таккера выведены также из предложения Лагранжа о переносе ограничений в целевую функцию. Таким образом, Кун и Таккер обобщили метод множителей Лагранжа на случай, когда система ограничений задачи нелинейного программирования включает неравенства, а такжеравенства и неравенства.

Имеются сведения о том, что задачу определения необходимых условий существования экстремума таких функций независимо от Гарольда Куна и Альберта Таккера решил в своей дипломной работе и будапештский студент Вильям Каруш.

В математическом анализе доказана теорема, определяющая необходимое условие локального экстремума функции нескольких переменных, которая утверждает, что для того чтобы локальный экстремум наблюдался в точке (х₁*,х₂*,…,х_n*), необходимо, чтобы в этой точке существовали конечные частные производные функции по каждой переменной и все они должны быть равны нулю, т.е.

.

Из этой теоремы вытекают два следствия:

1) если функция F(x₁,x₂,…,x_n) имеет в точке (х₁*,х₂*,…,х_n*) локальный экстремум и дифференцируема в этой точке, то ее дифференциал dF в этой точке обращается в нуль

dF(х₁*,х₂*,…,х_n*) = 0;

2) точки, в которых функция F(x₁,x₂,…,x_n) имеет локальный экстремум, следует устанавливать среди точек, где, либо одновременно все первые частные производные по переменным функции равны нулю

,

либо, по меньшей мере, одна из этих частных производных бесконечна или не существует.

Такие точки называются критическими. Однако не каждая критическая точка является точкой локального экстремума. Например, для функции F (x₁,x₂) = x₁x_2, точка с координатами (0,0) будет критической, т.к. первые частные производные обращаются в нуль в этой точке. Однако экстремума данной функции в этой точке нет. Действительно,

F (0,0) = 0, и можно получить точки сколь угодно близкие к точке (0,0), для которых как F(x₁,x₂) > 0, например, при х₁ > 0 и х₂ > 0, так и F(x₁,x₂) < 0, например, при х₁ > 0 и х₂ < 0 _. Соответствующая поверхность F(x₁,x₂) имеет вид седла (рис. 3).

 

F(x1,x2)

 

Рисунок 4 – Гиперболический параболоид F(x₁,x₂) = x₁x₂

 

В сечении поверхности F(x₁,x₂) плоскостью х₁ = х₂ получается парабола F(x₁,x₂) = х₁². Эта парабола имеет локальный минимум в точке (0,0). В сечении поверхности F(x₁,x₂) плоскостью х₁ = - х₂ получается парабола F(x₁,x₂) = - х₁² , которая имеет локальный максимум в точке (0,0). Таким образом, точка (0,0) является седловой точкой для функции F (x₁,x₂) = x₁x₂ , характерной тем, что через нее проходят как кривые, имеющие максимальное значение F(x₁,x₂) в этой точке, так и кривые имеющие в ней минимальное значение F(x₁,x₂).

Определение 7. Точка (X*, *) = (x₁*,x₂*,…x_n*; λ₁*, λ₂*, …, λ_m*) называется седловой точкой функции Лагранжа, если

L(x₁,x₂,…x_n; λ₁*, λ₂*, …, λ_m*) ≤ L(x₁*,x₂*,…x_n*; λ₁*, λ₂*, …, λ_m*) ≤

≤ L(x₁*,x₂*, …x_n*; λ₁, λ₂, …, λ_m) (5)

Теорема 2 (теорема Kyнa-Таккера).Для задачи нелинейного выпуклого nрограммирования (функции –ограничения – вогнуты, целевая функция –выпуклая или вогнутая), множество допусти­мых решений которой обладает свойством регулярности по Слейтеру, точка X ^* = (x₁*,x₂*,…x_n*) является оптимальным планом тогда и только тогда, когда существует такой вектор

* = ( λ₁*, λ₂*, …, λ_m*), (λ_i* ≥ 0, i = 1,2,…, m),

что (X*, *) – седловая точка функции Лагранжа.

Таким образом, необходимое условие локального максимума в точке стандартной задачи нелинейного выпуклого программирования формулируется следующим образом: пусть в точке х* выполняется модифицированное условие Слейтера. Тогда для наличия в ней условного локального максимума необходимо, чтобы в этой точке выполнялись условия Куна-Таккера.

Если функция Лагранжа L(X, ) дифференцируема по всем х и по всем λ, то теорему Куна -Таккера можно формально записать системой неравенств (условиями Каруша - Куна- Таккера), определяющей необходимые условия существования седловой точки функции Лагранжа (Х*, ), т. е. реше­ния задачи выпуклого программирования. Эти выражения имеют следующий вид:

 

(6)

где и значения соответствующих первых частных производ­ных функции Лагранжа, вычисленные в седловой точке.

 

Пример решения задачи выпуклого программирования с ограничениями - неравенствами

Задача 1. Фирма производит два вида товаров А и В. Для производства х₁ единиц товара А и х₂ единиц товара В требуется заранее приобрести

g(x₁,x₂) = x₁² + x₂² – x₁x₂ кг сырья. Из–за ограничений на объем склада количество заранее приобретенного сырья не должно превышать 2100 кг. Доход от реализации единицы товара А составляет 2000 руб., а от реализации товара В – 1000 руб.

Требуется принять обоснованное оптимальное решение по планированию производства товаров А и В, обеспечивающего фирме максимум дохода.

Решение.

1. Составим экономико - математическую модель задачи. Обоснование выбора метода решения.

Цель фирмы: получение максимального дохода, поэтому целевая функция имеет вид

F(x₁,x₂) = 2000 x₁ + 1000 x₂ → max,

в условиях ограничений:

g(x₁,x₂) = x₁² + x₂² – x₁x₂ ≤ 2100, (функциональное ограничение)

х₁ ≥ 0, х₂ ≥ 0 – (прямое ограничение)

Из анализа экономико-математической модели следует:

1) целевая функция линейна (вогнута и выпукла одновременно);

2) функциональное ограничение представлено нелинейной функцией – неравенством.

3) целевая функция и функция ограничение – непрерывны и дважды дифференцируемы.

Вывод: данная задача является задачей нелинейного программирования с ограничением неравенством. Такую задачу нельзя решить классическим методом множителей Лагранжа, но неизвестно можно ли ее решить методом множителей Лагранжа с применением теоремы Куна – Таккера.

2. Проверим функцию ограничение на выпуклость и регулярность (выполнение условия Слейтера).

Вычислим первые и вторые частные производные по х₁ и х₂:

; ; ; ; .

Получили матрицу Гессе

, Δ₁ = 2 > 0, Δ₂ = 3 > 0. Таким образом, функция ограничение является строго выпуклой (все угловые миноры матрицы Гессе больше нуля. Если, хотя бы один угловой минор равен 0 – нестрого выпуклая; если, хотя бы один угловой минор меньше нуля – невыпуклая (знакопеременная)).

Вывод: целевая функция линейная, т.е. вогнутая, функция ограничение – выпуклая – это задача выпуклого нелинейного программирования.

Проверим выполнение условия Слейтера.

Возьмем произвольную точку (х₁ = 1, х₂ = 1). В этой точке для функции ограничения выполняется условие (1 + 1 – 1< 2100), т.е. имеется, хотя бы одна точка в которой неравенство ограничение выполняется как строгое неравенство. Таким образом, условие регулярности Слейтера выполняется.

Общий вывод: условия Куна –Таккера являются необходимым и достаточным условием для наличия в любой точке области допустимых решений глобального максимума функции Лагранжа, а вместе с ней и исходной целевой функции.

3. Запишем функцию Лагранжа

L(x₁,x₂,λ) = 2000 x₁ + 1000 x₂ – λ (2100 – x₁² – x₂² + x₁x₂).

 

4. Запишем условия Куна -Таккера в алгебраическом виде:

, (a)

, (b)

, (c)

, (d)

, (e)

, (f)

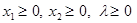. (k)

 

Такая система уравнений и неравенств решается, как правило, непросто. Однако в данном конкретном случае решение получается достаточно легко.

Из (a) и (k) следует, что λ ≠ 0 и х₁ ≠ 0. Из (b) и (k) следует, что х₂ ≠ 0.

Тогда из (c) получаем

, откуда

Из (d) ,

Следовательно .

Тогда ; ;

 

; . Подставим в (f) и получим

; ;

; ;

; х₁₁ = -50 (не подходит по условию задачи); х₁₂ = 50;

.

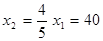Таким образом, оптимальным решением будет следующее: фирма должна выпускать 50 единиц продукции типа А и 40 единиц продукции типа В. При этом она получит доход

F(x₁,x₂) = 2000 x₁ + 1000 x₂ = 2000 * 50 + 1000 * 40 = 140 000 руб.