Определения
Уравнение вида:
Называют линейным (все производные функции y присутствуют в уравнении в первой степени) дифференциальным уравнением порядка n (порядок максимальной производной) с постоянными коэффициентам (
- не зависят от переменной)
В случае, когда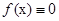 
уравнение называют однородным ЛДУ, иначе неоднородным ЛДУ
Пример:
Производная равна 0 для любого x, если функция постоянно, т.е. решением может являться любая константа.
Т.е. замечаем, что решением ЛДУ является не одна конкретная функция, а семейство функций (
)
Каждая функция, удовлетворяющая уравнению (например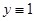 
), называется частным решением ЛДУ.
Совокупность всех функций, удовлетворяющих уравнению, называется общим решением ЛДУ
Общее решение неоднородного ЛДУ может быть представлено в виде суммы частного решения неоднородного ЛДУ и общего решения однородного ЛДУ.
Решение однородного ЛДУ
Решение однородного ЛДУ порядка n имеет вид:
Где 
- произвольные константы, а 
- решения уравнения:
Пример:
Решать уравнения, где есть повторяющиеся 
я вас не буду, ибо для решения физических задач это пока не пригодиться.
Решения неоднородного уравнения
Общий способ – искать решение уравнения
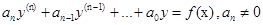
В виде:
Где - по-прежнему решения уравнения:
А 
- функции, которые находятся из прямой подстановки решения в уравнение (как в примере выше).
Однако иногда есть пути решения попроще, например:
Так же, как было сказано выше «Общее решение неоднородного ЛДУ может быть представлено в виде суммы частного решения неоднородного ЛДУ и общего решения однородного ЛДУ. »
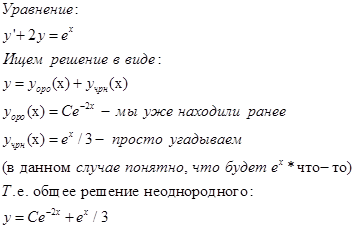
Граничные условия
Среди общего решения, нам порой нужно отобрать только одно, удовлетворяющее определенным условием, например, в уравнении 
, мы знаем, что 
т.е. в координате x=0 значение функции равно 1.
Собственно, премудростей никаких, находим общее решение, после этого подставляем в него условие:
Т.е. каждое условие сокращает количество свободных параметров на 1.
Соответственно, чтобы задать одну строго определенную функцию для уравнения порядка n нужно задать n условий.
Условия также могут быть на производные порядка не выше чем n-1. Т.е. в нашем случае мы можем также знать, например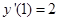 
, тогда^
Теперь мы знаем все что нужно!
Решение физических задач
Грузик массой m на пружинке с жесткостью k выведен из положения равновесия на величину A и отпущен. Найти зависимость координаты от времени.
Грузик массой m на пружинке с жесткостью k погружен в воду, и выведен из положения равновесия толчком так, что начальная скорость равна v. Сила сопротивления в воде F = -av(t)
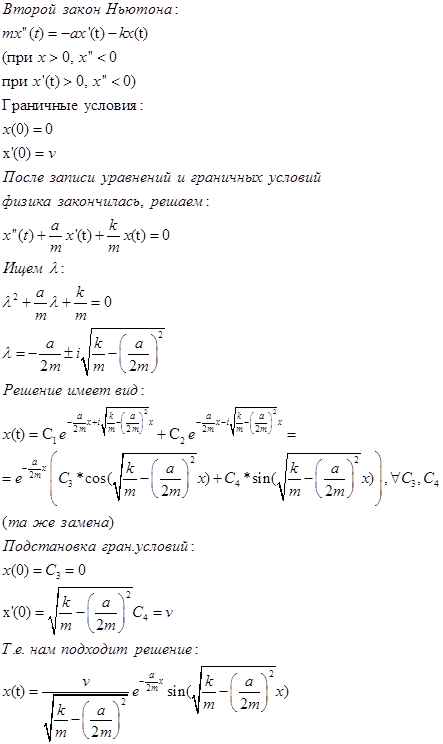
Обычно, что затухание слабое 
, по этому я представил все в виде тригонометрических функций. Добавка вязкого трения приводит к экспоненциальному уменьшению амплитуды колебаний и небольшому увеличению периода.
Если бы затухание было велико, то была бы чистая экспонента (произошло бы меньше одного колебания)
Напоследок:
Дана электрическая цепь из последовательно соединенных источника напряжения E, резистора R, конденсатора емкостью C и ключа. В момент времени t=0 конденсатор не заряжен, и замыкают ключ. Найти зависимость тока в цепи от времени.
Т.е. ток в цепи экспоненциально убывает во времени, а конденсатор также экспоненциально заряжается до определенного значения.
Ура, товарищи!