Задачи типа J характеризуются одной ситуацией, наличием одного критерия и индивидуальным ЛПР. Информация, описывающая задачи такого типа характеризуется следующими исходными данными:
- известно множество альтернатив A = (a1,a2,…,an);
- однозначно вычисляется значение функции предпочтения (полезности) для каждой альтернативы F = (f1.f2,…,fn).
Формально такая задача задается матрицей вида
| Альтернативные решения | a1 | a2 | … | an |
| Значения функции предпочтения | f1 | f2 | … | fn |
Для вычисления значений функции предпочтения по каждой альтернативе может быть использована любая шкала: порядковая (ранги), количественная (степени достижения) и т.д. В дополнение к этой матрице может использоваться другая информация об особенностях решения задачи, условиях, ограничениях на ресурсы, возможностях и т.д.
Если на множестве исходов Y задан критерий эффективности K(a), то с его помощью можно характеризовать непосредственно сами стратегии: стратегии a будет соответствовать значение критерия К (ψ (a)).
Поэтому в задачах выработки решений в условиях определенности под критерием можно понимать числовую функцию К(a), определенную на множестве стратегий A.
Если эффективность стратегий удается достаточно полно оценить при помощи одного критерия, то такие задачи называются однокритериальными.
Выбор (построение) единственного критерия эффективности должен осуществляться с учетом ряда специальных требований. Обычно считается, что должны выполняться следующие требования:
1) соответствие. Критерий должен соответствовать смыслу (существу) поставленной задачи;
2) полнота. Критерий должен обладать функциональной полнотой (т. е. учитывать все существенные для решения поставленной задачи технические, экономические и другие факторы);
3) критичность. Критерий должен быть достаточно чувствительным к переменным параметрам задачи;
4) содержательность. Критерий должен иметь «физический смысл» (это упрощает анализ, интерпретацию полученных результатов и формулировку рекомендаций);
5) вычислимость. Значения критерия должны достаточно просто вычисляться (это обеспечивается, например, представлением критерия относительно простым аналитическим выражением).
Одним из важнейших среди перечисленных требований является первое. Оно впервые было четко сформулировано в виде так называемого «принципа соответствия» в статье академика Колмогорова «Число попаданий при нескольких выстрелах и общие принципы оценки эффективности систем стрельбы». Труды института им. Стеклова, 1945,№2.
Естественно, что требование «5)» ориентировано исключительно только на количественные критерии.
В большинстве практических задач в качестве критерия выбираются такие функции, для которых либо большее значение всегда предпочтительнее меньшего, либо, наоборот, меньшее значение предпочтительнее большего.
В первом случае критерий часто имеет смысл прибыли, дохода и т. п., выражает степень достижения поставленной цели (например, процент выполнения планового задания) или же отражает «технические» характеристики, которые желательно увеличивать (скажем, удобство работы оператора, которое может оцениваться экспертами в баллах).
Во втором случае критерий имеет смысл издержек, расхода ресурсов и т. п. или же описывает «технические» характеристики, которые желательно минимизировать (скажем, шумы двигателя самолета гражданской авиации).
В однокритериальной задаче при указанном направлении предпочтительного изменения значений критерия фактически оказывается введенной функция ценности, и понятие оптимальной стратегии определяется очень просто: если большие значения критерия предпочтительнее меньших, то оптимальной является стратегия a*, максимизирующая критерий
K(u*) = mах К (и); (1)
и  U
U
если же, наоборот, меньшие значения критерия предпочтительнее больших, то оптимальной является стратегия, минимизирующая критерий
K(u*)=min K(u). (2)
и  U
U
Таким образом, определение понятия оптимальной стратегии в однокритериальных задачах выработки решений в условиях определенности в большинстве случаев никаких принципиальных трудностей не вызывает. Однако это не значит, конечно, что практическое вычисление оптимальной стратегии всегда осуществляется достаточно просто. Наоборот, реальные задачи определения (1) и (2) в вычислительном отношении оказываются обычно весьма сложными, и для их решения приходится использовать ЭВМ и специальные методы оптимизации, выбор которых определяется конкретными особенностями задачи, требованиями к точности решения, наличием времени и т. п.
Не следует, однако, думать, что всякая однокритериальная задача легко представляется в виде задачи максимизации или же минимизации путем задания единого направления возрастания предпочтений для всей шкалы критерия. Иногда для такого представления может потребоваться более детальная информация о предпочтениях.
Рассматриваемый класс задач обоснования решений по скалярному показателю в условиях определенности имеет важное практическое значение по следующим причинам:
1) задачи данного типа довольно часто встречаются на практике;
2) многие задачи обоснования решений по векторному показателю в условиях неопределенности могут быть формально сведены (и обычно сводятся) к схеме задачи обоснования решения по скалярному показателю в условиях определенности или декомпозированы на ряд таких задач;
3) методы решения данного типа задач позволяют лучше понять и помогают создавать и развивать методологию решения более сложных задач.
Таким образом, задача обоснования решений по скалярному показателю в условиях определенности после задания основных ее элементов (вида показателя и типа критерия эффективности, функционального задания исходного множества стратегий и модели «стратегия-показатель») трансформируется в задачу выбора той допустимой альтернативы, которая обращает в максимум (минимум) целевую функцию (функцию полезности). Детализируем постановку задачи выбора.
Мы уже отметили, что стратегия ЛПР представляет собой установленный им порядок использования активных ресурсов и может формально представляться некоторым набором (вектором) X = { xi } существенных управляемых параметров таких, как параметры структуры или последовательности выполнения отдельных элементарных операций, функциональные и конструктивные параметры и др.
Формальное представление исходного множества допустимых стратегий А* обычно производится заданием ограничений G* на значения компонент вектора Х управляемых параметров.
Следует отметить, что построение любой математической модели ЗПР почти всегда связано с необходимостью удовлетворения двух, по существу, противоположных требований:
- как можно точнее отразить изучаемые реальные явления;
- построить достаточно простую математическую модель для решения ЗПР.
Именно поэтому на этапе построения математической модели необходимо тесное сотрудничество исследователя операции (математика, научного сотрудника, инженера) и ЛПР (специалиста в проблемной ситуации, руководителя, менеджера).
Связь характеристик X управляемых параметров исследуемого физического процесса и ограничений, связанных с обеспечением их физической реализуемости и гибкости, в виде равенств или неравенств  , определяет область допустимых значений (ОДЗ) X* управляемых параметров, и имеет форму функциональной зависимости
, определяет область допустимых значений (ОДЗ) X* управляемых параметров, и имеет форму функциональной зависимости  , называемую целевой функцией при наложенных на нее уравнениях-ограничениях
, называемую целевой функцией при наложенных на нее уравнениях-ограничениях  :
:
 (3)
(3)
При геометрических представлениях ОДЗ любой ее вектор X* удовлетворяющий условию (3), называется допустимой точкой.
В зависимости от конкретного вида целевой функции  и ограничений
и ограничений  задача выбора (3) относится к одному из типов оптимизационных задач, для которых имеются свои эффективные методы решения.
задача выбора (3) относится к одному из типов оптимизационных задач, для которых имеются свои эффективные методы решения.
Следует отметить, что если размерность задачи невысока, а целевая функция и ограничения аналитические, то в подавляющем большинстве случаев решение может быть найдено классическими аналитическими методами: полного перебора, математического анализа, неопределенных множителей Лагранжа и др.
При высокой размерности задачи, а также сложном виде целевой функции и уравнений-ограничений, используют численные методы, требующие применения ЭВМ и специального математического обеспечения. К этой группе методов относятся процедуры и алгоритмы математического программирования.
В особо сложных случаях используются методы вариантного анализа (вариационного исчисления), каждый из которых реализует серию перемежающихся формальных и эвристических процедур. В ходе вариантного анализа ЛПР и исследователи осуществляют последовательное сужение множества допустимых вариантов. На первом этапе ЛПР и эксперты эвристически формируют множество опорных стратегий, по их мнению, более предпочтительных, чем любые другие. В выбранных точках определяют значения показателя эффективности. Проанализировав полученную информацию, вновь формируют множество опорных точек в области предполагаемого экстремума. Процесс заканчивается, когда ЛПР удовлетворено полученными результатами.
Таким образом: в ЗПР в условиях определенности по способу получения значения х* различают:
1) классические методы оптимизации, основанные на использовании необходимых и достаточных условий экстремума целевой функции и сводящие исходную задачу к задаче поиска решения в общем случае системы трансцендентных уравнений;
2) прямые (релаксационные) методы, в которых х* устанавливается путем построения сходящейся последовательности точек, принадлежащих Х*.
Методика решения задач однокритериальной оптимизации предполагает последовательное выполнение следующих этапов:
- этап 1 – постановка задачи (формальное задание экономико-математической модели);
- этап 2- выбор метода решения задачи;
- этап 3 – решение задачи выбранным методом;
- этап 4 – анализ и интерпретация результатов.
3 Пример решения задачи принятия решения в условиях определенности (линейная задача оптимального планирования производства)
Предприятие может выпускать четыре вида продукции, используя для этого три вида ресурсов. Достоверно известны:
- технологическая матрица А затрат каждого из ресурсов на единицу каждой продукции
А =  ;
;
- вектор - столбец b – объема имеющихся ресурсов
b =  ;
;
- вектор –строка цен (неизменных) на все виды продукции
с = (36 14 25 50).
Требуется принять решение по определению оптимальной производственной программы, обеспечивающей предприятию наибольшую выручку (но не менее 2000 усл.ед) (не прибыль) при имеющихся ограниченных ресурсах. Предполагается, что спрос на все виды продукции неограничен.
Решение.
Этап 1. Составление экономико-математической модели:
- требуется вычислить вектор, определяющий производственную программу
х =  ,
,
где хi - количество выпускаемой продукции i-го вида;
- максимизирующего выручку
F(X) = c1 x1 + c2 x2 + c3x3 + c4 x4 = 36x1 + 14x2 + 25x3 + 50x4 (целевая функция)
при ограничениях на ресурсы

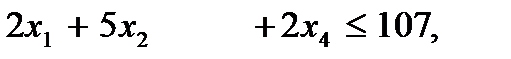

- по экономическому смыслу задачи предприятие не может выпускать отрицательное количество любого вида продукции, поэтому запишем стандартные ограничения
x1, x2, x3, x4 ≥ 0.
Этап 2. Выбор метода решения задачи
В результате анализа модели имеем:
1) целевая функция и функции ограничений – линейны;
2) стандартные ограничения присутствуют;
вывод: данная задача относится к классу задач линейного программирования;
3) переменных в задаче – четыре (больше двух). Следовательно, такую задачу необходимо решать симплекс-методом.
Приведение задачи к канонической форме:
- целевая функция – на максимум (изменений не требуется);
- перейдем от ограничений неравенств к ограничениям – равенствам, введя дополнительные переменные х5,х6, х7 с положительным знаком, т.к. все ограничения вида ≤. Дополнительные переменные имеют смысл остатков ресурсов, соответственно, первого, второго и третьего видов.
Получим систему ограничений – равенств:


 .
.
С точки зрения математики необходимо среди всех решений данной системы уравнений вычислить те решения, которые удовлетворяют условиям неотрицательности x1, x2, x3, x4 , х5, х6, х7 ≥ 0 и обращают в максимум целевую функцию.
Этап 3. Решение задачи линейного программирования методом симплекс-таблиц.
Запишем систему ограничений –равенств в векторной форме
Р1 =  , Р2 =
, Р2 =  , Р3 =
, Р3 =  , Р4 =
, Р4 = 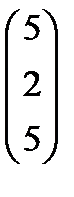 , Р5 =
, Р5 =  , Р6 =
, Р6 = 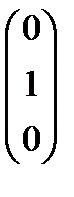 , Р7 =
, Р7 =  , Р0 =
, Р0 = 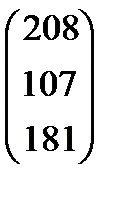
Из анализа векторов следует, что среди них имеется три (равно числу уравнений функций ограничений) единичных ортогональных вектора Р5, Р6 , Р7 , поэтому они автоматически составляют первоначальный базис.
Составим первую симплекс – таблицу.
Таблица 1 - Исходная симплекс -таблица
| i | Базис | сб | P0 | |||||||
| P1 | P2 | P3 | P4 | P5 | P6 | P7 | ||||
| P5 | 208 | |||||||||
| P6 | ||||||||||
| P7 | ||||||||||
| -36 | -14 | -25 | -50 |
По критериям, принятым в симплекс-методе данное решение является допустимым (все хi ≥ 0, а именно: х1 = 0, х2 = 0, х3 = 0, х4 = 0, х5 = 208, х6 = 107, х7 = 181), но не оптимальным (в индексной (четвертой) строке имеются отрицательные значения).
Выполним первое симплекс-преобразование.
Наибольшее по абсолютной величине отрицательное значение (- 50) находится в столбце вектора Р4, следовательно, этот столбец становится разрешающим и должен быть введен в новый базис. Для определения разрешающей строки (строки, которая должна быть выведена из базиса) вычислим отношение  для разрешающего столбца и выберем из него минимальное:
для разрешающего столбца и выберем из него минимальное:
min {  } = min {
} = min { 
По этому правилу минимальным является отношение  , что соответствует строке 3. Таким образом, из базиса должна быть выведена строка 3, т.е. строка вектора Р7 (строка 3 является разрешающей).
, что соответствует строке 3. Таким образом, из базиса должна быть выведена строка 3, т.е. строка вектора Р7 (строка 3 является разрешающей).
На пересечении разрешающей строки и разрешающего столбца находится разрешающий элемент ар = 5.
Построим новую симплекс-таблицу (таблица 2).
Таблица 2 - Первая симплекс -таблица
| i | Базис | сб | P0 | |||||||
| P1 | P2 | P3 | P4 | P5 | P6 | P7 | ||||
| P5 | -1 | |||||||||
| P6 | 173/5 | 4/5 | 23/5 | -4/5 | -2/5 | |||||
| P4 | 181/5 | 3/5 | 1/5 | 2/5 | 1/5 | |||||
| - 6 | - 4 | - 5 |
Заполним столбцы нового базиса (Р4,Р5,Р6).
Заполним элементы разрешающей строки, разделив старые значения на значение разрешающего элемента ар = 5.
Вычислим свободные элементы информационных строк, используя правило треугольника:
b50Н = b50С – а54С b40Н = 208 – 5 181/5 = 27.
Аналогично заполним остальные свободные клетки.
Рассчитаем элементы индексной строки:
b40 = F(X) = 0 27 + 0 173/5 + 50 181/5 = 1810.
a41 = 0 1 + 0 4/5 + 50 3/5 – 36 = - 6. Остальные аналогично.
Из анализа полученного решения следует:
1) значение целевой функции существенно увеличилось;
2) полученное решения является допустимым (х1 = 0, х2 = 0, х3 = 0, х4 = 181/5, х5 = 27, х6 = 173/5, х7 = 0), но не оптимальным (в индексной (четвертой строке имеются отрицательные значения).
Выполним второе симплекс-преобразование.
Наибольшее по абсолютной величине отрицательное значение (- 6) находится в столбце вектора Р1, следовательно, этот столбец становится разрешающим и должен быть введен в новый базис. Для определения разрешающей строки (строки, которая должна быть выведена из базиса) вычислим отношение  для разрешающего столбца и выберем из него минимальное:
для разрешающего столбца и выберем из него минимальное:
min {  } = min {
} = min { 
По этому правилу минимальным является отношение  , что соответствует строке 1. Таким образом, из базиса должна быть выведена строка 1, т.е. строка вектора Р5 (строка 1 является разрешающей).
, что соответствует строке 1. Таким образом, из базиса должна быть выведена строка 1, т.е. строка вектора Р5 (строка 1 является разрешающей).
На пересечении разрешающей строки и разрешающего столбца находится разрешающий элемент ар = 1.
Построим новую симплекс-таблицу (таблица 3).
Таблица 3 - Вторая симплекс -таблица
| i | Базис | сб | P0 | |||||||
| P1 | P2 | P3 | P4 | P5 | P6 | P7 | ||||
| P1 | -1 | |||||||||
| P6 | -12/5 | -45 | 2/5 | |||||||
| P4 | -1 | -4/5 | -3/5 | |||||||
Заполним столбцы нового базиса (Р1,Р6,Р4).
Заполним элементы разрешающей строки, разделив старые значения на значение разрешающего элемента ар = 1.
Вычислим свободные элементы информационных строк, используя правило треугольника
Рассчитаем элементы индексной строки:
Из анализа полученного решения следует:
1) значение целевой функции еще увеличилось;
2) полученное решения является допустимым (х1 = 27, х2 = 0, х3 = 0, х4 = 20, х5 = 0, х6 = 13, х7 = 0) и оптимальным.
Таким образом, оптимальной программой для предприятия является:
производить:
- продукции первого вида х1 = 27 единиц;
- продукцию второго и третьего вида не производить х2 = 0, х3 = 0;
- продукции четвертого вида х4 = 13 единиц.
При этом наибольшая выручка составит 1972 усл.ед, что меньше, чем требуемая 2000 усл.ед, т.е. конечная цель не достигнута. Недостача составляет Δ = 2000 – 1972 = 28 усл.ед.
Таким образом, первая альтернатива а1 (первое решение) – отказаться от производства этих товаров.
Вторая альтернатива а2 - изыскать дополнительные ресурсы и с учетом этого производить данные товары. При этом естественно возникает вопрос: какие ресурсы и на сколько необходимо увеличить, чтобы добиться поставленной цели? Ответ на этот вопрос должен дать четвертый этап.
Этап 4. Анализ и интерпретация результатов.
Оценочные коэффициенты Δ1, Δ2 , Δ3 , Δ4 (элементы индексной строки окончательного решения) имеют смысл оценок технологий и показывают, насколько уменьшится выручка, если произвести дополнительно единицу соответствующей продукции. Например, коэффициент Δ3 = 7 показывает, что если дополнительно произвести одну единицу продукции третьего вида (она не входит в оптимальную производственную программу), то общая выручка уменьшится на 7 усл. ед.
Оставшиеся коэффициенты Δ5, Δ6 , Δ7 имеют смысл двойственных оценок ресурсов и показывают, насколько возрастет выручка, если первоначальные запасы соответствующего ресурса увеличить на единицу. Так, увеличение на единицу запаса первого ресурса приведет к увеличению выручки на Δ5 = 6 усл. ед., третьего ресурса – на 4 усл.ед. Следовательно, можно рассматривать следующие альтернативы:
а3 - увеличить объем первого ресурса на (28: 6) = 5 ед. (с 208 до 213 ед.);
а4 - увеличить объем третьего ресурса на (28: 4) = 7 ед.(с 181 до 188 ед.);
а5 - одновременно увеличить объемы первого и третьего ресурсов в соответствующих пропорциях, например, первого – на 3 ед. (получим прирост выручки 3 х 6 = 18 ед.) и третьего – на 3 ед. (получим прирост выручки 3 х 4 = 12 ед.), что даст в итоге требуемый прирост выручки в 30 ед.
Отметим, что для автоматизации и существенного ускорения процесса решения задач такого типа в ППП EXCEL разработана специальная надстройка, которая имеет называние Solver (русскоязычное название «Поиск решения»). Практические приемы использования этой надстройки рассматриваются на соответствующем практическом занятии.
* * *
МОР – ПЗ7 – Э31
Министерство образования и науки Российской Федерации
Федеральное государственное бюджетное образовательное учреждение
высшего образования
«Российский государственный гуманитарный университет»