Найти реакции опор конструкции. Схемы конструкций представлены на рисунке 1 (размеры — в м), нагрузка указана в таблице 1.
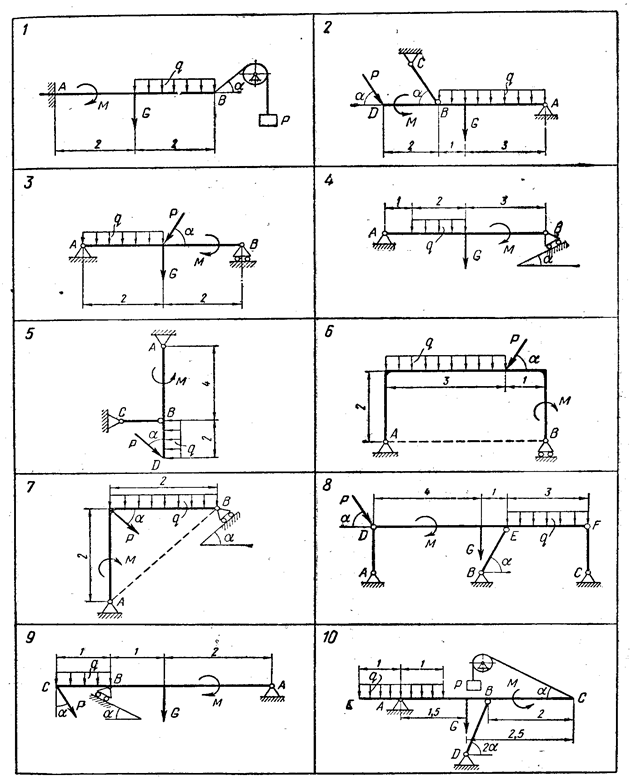
Рисунок 1 – Варианты задачи С-1
Таблица 1– Исходные данные к задаче С-1.
| Номер варианта | Номер рисунка | G | P | М, кНм | q, кН/м | a, град |
| кН | ||||||
| - | ||||||
| - | ||||||
| - | ||||||
| - | ||||||
| - | ||||||
| - | ||||||
| - | ||||||
| - | ||||||
| - | ||||||
| - | ||||||
| - | ||||||
| - | ||||||
Пример выполнения задания:
Дано: схема конструкции рисунок 1; G = 10 кН; Р = 5 кН; М = 8 кНм; q = 0,5 кН/м; α =30°; размеры - в м.
Определить реакцию опоры А и реакцию стержня CD.
Р е ш е н и е:
Рассмотрим уравновешенную систему сил, приложенных к балке АВ.

| Действие связей на балку заменяем их реакциями (рисунок 2). Так как направление реакции шарнирно- неподвижной опоры А неизвестно, то определяем ее составляющие 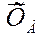 и и  . .
|
 Рисунок 2
Рисунок 2

 Покажем также реакцию
Покажем также реакцию  стержня CD и реакцию
стержня CD и реакцию  нити, модуль которой равен Р. Равномерно-распределенную нагрузку интенсивностью q, заменяем сосредоточенной силой Q,, равной Q = 2× q = 2× 0,5 = 1 кН и приложенной в центре тяжести эпюры этой нагрузки.
нити, модуль которой равен Р. Равномерно-распределенную нагрузку интенсивностью q, заменяем сосредоточенной силой Q,, равной Q = 2× q = 2× 0,5 = 1 кН и приложенной в центре тяжести эпюры этой нагрузки.
 Для плоской системы сил, приложенных к балке, составляем три уравнения равновесия:
Для плоской системы сил, приложенных к балке, составляем три уравнения равновесия:
 |
Рисунок 3
 = 0; - Q × 1 – G × 3+SCD × 4sin30° - M + T × 6 = 0; (1)
= 0; - Q × 1 – G × 3+SCD × 4sin30° - M + T × 6 = 0; (1)
 =0; XA - Scd cos 30° = 0; (2)
=0; XA - Scd cos 30° = 0; (2)
 =0; Ya - Q - G + SCD cos 60° + T = 0; (3)
=0; Ya - Q - G + SCD cos 60° + T = 0; (3)
Из уравнения (1):
 кН.
кН.
Из уравнения (2):
ХA = SCD cos 30° = 3,90 кН.
Из уравнения (3):
Ya = Q + G —SCD cos 60° - T= 1+ 10 - 4,5 • 0,5 - 5 = 3,75 кН.
Значения ХА, YA, SCD получаются положительными. Это указывает на то, что принятые направления этих сил совпадают с их действительными направлениями.
Задача К-1 «Кинематический анализ плоского механизма»
Кривошип ОА вращается вокруг неподвижной оси, имея данный момент времени угловую скорость w ОА и угловое ускорение e ОА. Найти для заданного положения механизма скорости и ускорения точек А, В, С, а также угловую скорость и угловое ускорение звена АВ. Схемы механизмов представлены на рисунке 4, данные к задаче в таблице 2.


 |
 |
| а) | б) |

в)
Рисунок 4 – Схемы механизмов к задаче К-1.
Таблица 2 – Исходные данные к задаче К-1.
| № варианта | Схема | Угол a0, град. | Угол γ, град. | Размеры, см | wОА, рад/с | eОА, рад/с2 | ||
| ОА | АВ | АС | ||||||
| а | - | -2 | ||||||
| б | ||||||||
| в | -3 | |||||||
| а | - | |||||||
| б | -4 | |||||||
| в | ||||||||
| а | - | -5 | ||||||
| б | ||||||||
| в | -2 | |||||||
| а | - | |||||||
| б | -3 | |||||||
| в | ||||||||
| а | - | -4 | ||||||
| б | ||||||||
| в | -6 | |||||||
| а | - | |||||||
| б | -8 | |||||||
| в | ||||||||
| а | -10 | |||||||
| б | ||||||||
| в | -5 | |||||||
| а | - | |||||||
| б | -4 | |||||||
| в | ||||||||
| а | - | -3 | ||||||
| б | ||||||||
| в | -2 | |||||||
| а | - | |||||||
| б | -4 | |||||||
| в |
Пример выполнения задания:
Дано: схема механизма (рисунок 4); ОА = 0,3 м; АВ = 0,7 м; АС = СВ; wОА = 2 рад/с; eОА = 1 рад/с2; a=150°; g=60°. Определить угловую скорость, угловое ускорение звена АВ и линейные скорости, ускорения точек А, В, С.
Р е ш е н и е:
1. Определение скоростей точек и угловой скорости звена АВ (рисунок 6).
 |
Рисунок 5 Рисунок 6
В кривошипно-шатунном механизме кривошип ОА совершает вращательное движение, ползун В – поступательное, шатун АВ – плоское движение.
2. Определим скорость точки А, считая, что она принадлежит кривошипу:
 = wОА . ОА = 2 . 0,3 = 0,6 м/с.
= wОА . ОА = 2 . 0,3 = 0,6 м/с.
Вектор  направлен ^ ОА в сторону вращения кривошипа.
направлен ^ ОА в сторону вращения кривошипа.
1-й способ.Найдем скорость точки В звена АВ, выбрав за полюс точку А. Скорость ползуна В направлена вдоль направляющих ползуна по вертикали. За полюс выберем точку А, скорость которой известна. По теореме сложения скоростей определим  :
:
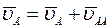 . (4)
. (4)
Спроектируем (4) на оси Х, Y, имея ввиду, что  ^АВ:
^АВ:
 сos 600 =
сos 600 =  сos 300, (5)
сos 300, (5)
 сos 300 =
сos 300 =  sin 300 +
sin 300 +  . (6)
. (6)
Из уравнения (5) находим скорость  = 1,04 м/с2, из уравнения (6) определяем
= 1,04 м/с2, из уравнения (6) определяем  = 0,6 м/с.
= 0,6 м/с.
Зная, что  = wАВ . АВ, определяем wАВ = 0,86 рад/с.
= wАВ . АВ, определяем wАВ = 0,86 рад/с.
Скорость точки С найдем двумя способами, выбрав за полюс точку А, а затем точку В:
а) за полюс выберем точку А (рисунок 7).
По теореме сложения скорстей:
 , (7)
, (7)
где 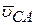 ^ АВ и направлена в сторону вращения звена АВ. Спроектируем (7) на оси Х, Y:
^ АВ и направлена в сторону вращения звена АВ. Спроектируем (7) на оси Х, Y:
 СХ =
СХ =  Аcos 300,
Аcos 300,
 CY =
CY =  A sin 300 +
A sin 300 +  CA.
CA.

Рисунок 7
Подставляя данные и учитывая, что 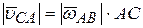 = 0,86 . 0,35 = 0,3 м/с,
= 0,86 . 0,35 = 0,3 м/с,
получим  СХ = 0,52 м/с;
СХ = 0,52 м/с;  CY = 0, 6 м/с. По теореме Пифагора определяем
CY = 0, 6 м/с. По теореме Пифагора определяем  C = 0,79 м/с.
C = 0,79 м/с.
б) за полюс выберем точку В (рисунок 8). По теореме сложения скоростей:
 , (8)
, (8)
где  ^ АВ и направлена в сторону вращения звена АВ. Спроектируем (8) на оси Х, Y:
^ АВ и направлена в сторону вращения звена АВ. Спроектируем (8) на оси Х, Y:
 СХ =
СХ =  В cos600,
В cos600,
 =
=  B cos300 -
B cos300 -  CB.
CB.

Рисунок 8
Подставляя данные и учитывая, что  , получим:
, получим:  СХ = 0,52 м/с;
СХ = 0,52 м/с;  СY = 0,6 м/с;
СY = 0,6 м/с;  С = 0,79 м/с.
С = 0,79 м/с.
2-й способ. Определим 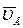 ,
,  ,
,  с помощью МЦС. Для нахождения
с помощью МЦС. Для нахождения
МЦС строим перпендикуляры к скоростям в точках А и В. Точка Р является МЦС звена АВ (рисунок 9).
Для нахождения угловой скорости звена АВ разделим скорость точки А на АР (АР = АВ, т.к. треугольник АРВ – равнобедренный)
 =
= 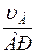 = 0,86 рад/с. (9)
= 0,86 рад/с. (9)
Скорость точки С направлена перпендикулярно РС в сторон вращения звена АВ. Модуль скорости  С определим по формуле:
С определим по формуле:
 |
Рисунок 9

 СР = 0,79 м/с.
СР = 0,79 м/с.
Длину СР определяем по теореме косинусов:
СР =  = 0,93 м.
= 0,93 м.
Для нахождения скорости точки В определим РВ из треугольника РАВ:
РВ = 2 АВcos 300 = 1,21 м.
Модуль скорости точки В определим по формуле:
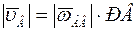 = 1,04 м/с.
= 1,04 м/с.
Вектор  направлен перпендикулярно РВ в сторону вращения звена АВ (по вертикали вниз).
направлен перпендикулярно РВ в сторону вращения звена АВ (по вертикали вниз).
3-й способ. По теореме о проекциях скоростей точек на ось, проходящую через эти точки, имеем:
 ,
,
 300 =
300 = 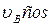 600.
600.
Откуда  = 1,04 м/с.
= 1,04 м/с.
II. Определение ускорений точек и углового ускорения звена АВ. Для нахождения ускорений точек В и С воспользуемся ткоремой сложения ускорений:
 , (10)
, (10)
где А – полюс.
Так как направление ускорения ползуна В известно (по вертикали), определим сначала ускорение точки В, а затем ускорение точки С. За полюс выберем точку А, т.к. ускорение этой точки, используя данные задачи, можно определить. Точка А принадлежит кривошипу ОА, совершающему вращательное движение, поэтому:
 . (11)
. (11)
 (12)
(12)
Ускорение точки В определяем по формуле:
 . (13)
. (13)
В этом соотношении известно направление касательного ускорения точки В вокруг А (перпендиклярно АВ).
Найдем нормальное ускорение точки В при вращении вокруг А
 АВ = 0,862 . 0,7 = 0,52 м/с2.
АВ = 0,862 . 0,7 = 0,52 м/с2.
Изобразим векторы соотношения (13) на чертеже, получим многоугольник из ускорений (рисунок 10). Выберем оси координат и спроектируем (13) на эти оси:
Х: аВ cos600 = -  , (14)
, (14)
Y: aB sin600 =  . (15)
. (15)
 |
Рисунок 10
Из уравнения (14) находим:
аВ =  = 0,36 м/с2.
= 0,36 м/с2.
Из уравнения (15) находим:
 = 0,85 м/с2.
= 0,85 м/с2.
Угловое ускорение eАВ находим по формуле:
eАВ =  = 1,2 рад/с2. (16)
= 1,2 рад/с2. (16)
Направление eАВ соответствует  .
.
Находим ускорение точки С, выбрав за полюс точку А:
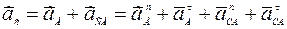 . (17)
. (17)
Модули ускорений  и
и  найденные выше (см. соотношения (12)). Угловая скорость и угловое ускорение звена АВ определяют соотношения (9) и (16).
найденные выше (см. соотношения (12)). Угловая скорость и угловое ускорение звена АВ определяют соотношения (9) и (16).
Ускорения точки С при вращении вокруг А находим по формулам:
 АС = 0,862 . 0,35 = 0,26 м/с2;
АС = 0,862 . 0,35 = 0,26 м/с2;
 . АС = 1,2 + 0,35 = 0,42 м/с2.
. АС = 1,2 + 0,35 = 0,42 м/с2.
Изобразим все составляющие ускорения точки С на чертеже и спроектируем (17) на оси Х, Y (рисунок 11):
а СХ= 
aCY = 
 |
Рисунок 11
После подстановки ранее полученных результатов имеем:
аСХ = 0;
аCY = 0,77 м/с2.
Модуль ускорения точки С находим по теореме Пифагора:
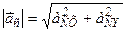 = 0,77 м/с2.
= 0,77 м/с2.

Рисунок 12