Механическая система под действием сил тяжести приходит в движение из состояния покоя; начальное положение системы показано на схемах а-и Приложения А. Учитывая трение скольжения тела 1 (схемы а-е, з-к) и сопротивление качению тела 3, катящегося без скольжения (схемы б, г, е-и), пренебрегая другими силами сопротивления и массами нитей, предполагаемых нерастяжимыми, определить скорость тела 1 в момент, когда пройденный им путь станет равным S.
В задании приняты следующие обозначения: m1, m2,m3,m4 – массы тел 1, 2, 3, 4; R2, r2, R3 r3 – радиусы больших и малых окружностей; i2x, i3x – радиусы инерции тел 2 и 3 относительно горизонтальных осей проходящих через их центры тяжести; a и b - углы наклона плоскостей к горизонту; f – коэффициент трения скольжения; d - коэффициент трения качения.
Необходимые для решения данные приведены в таблице 2. Блоки и катки, для которых радиусы инерции в таблице не указаны, считать сплошными однородными цилиндрами.
Наклонные участки нитей параллельны соответствующим наклонным плоскостям.
Приложение А
Схемы заданий к задаче Д-2

(а)

(б)

(в)
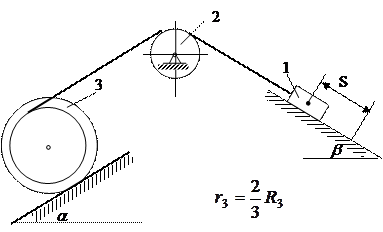
(г)
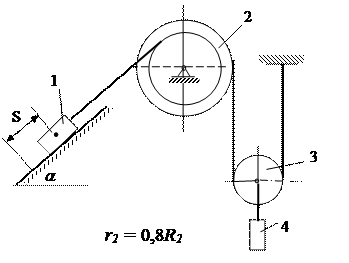
(д)
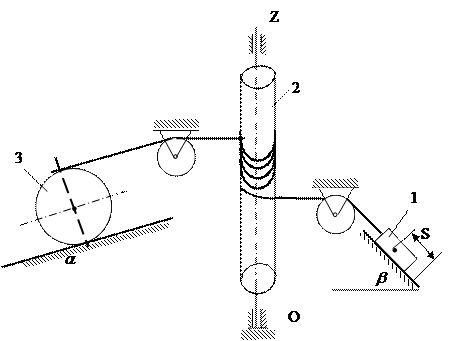
(е)
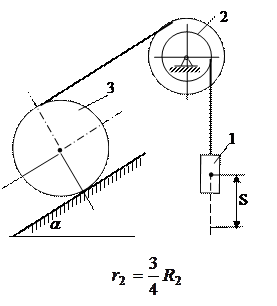
(ж)

(з)
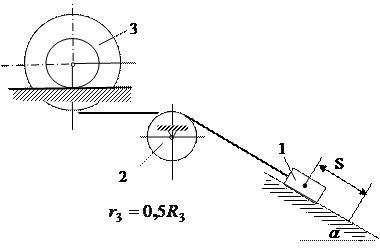
(и)
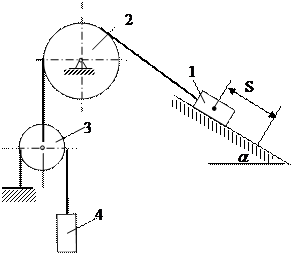
(к)
Таблица 2– Исходные данные к задаче Д-2
| № варианта | № с х е мы | m1 | m2 | m3 | m4 | R2 | R3 | i2x | i3x | a | b | f | d, см | S, м | |
| кг | cм | см | град | ||||||||||||
| а | m | 4 m | 1/5m | 4/3m | - | - | - | - | - | 0,10 | - | ||||
| б | m | ½ m | 1/3m | - | - | - | 0,22 | 0,20 | |||||||
| в | m | m | 1/10m | m | - | - | - | - | - | 0,10 | - | ||||
| г | m | ½ m | 1/4m | - | - | 0,17 | 0,20 | 2,5 | |||||||
| д | m | 1/3m | 1/10m | - | - | - | - | 0,15 | - | 1,5 | |||||
| е | m | 3m | m | - | - | - | - | 0,10 | 0,28 | 1,5 | |||||
| ж | m | 2m | 2 m | - | - | - | - | 0,20 | |||||||
| з | m | ½ m | 1/3m | - | - | - | - | 0,15 | 0,20 | 1,75 | |||||
| и | m | 2m | 9m | - | - | - | - | 0,12 | 0,25 | 1,5 | |||||
| к | m | 1/4m | 1/4m | 1/5m | - | - | - | - | - | 0,10 | - | ||||
| а | m | 3m | 1/4m | 2/3m | - | - | - | - | - | 0,15 | - | 1,8 | |||
| б | m | 1/3m | 1/4m | - | - | - | 0,20 | 0,30 | |||||||
| в | m | 2m | 1/5m | 1/8m | - | - | - | - | - | 0,15 | - | 2,5 | |||
| г | m | 1/3m | 1/5m | - | - | - | 0,20 | 0,25 | |||||||
| д | m | ½ m | 1/12m | m | - | - | - | 0,10 | - | ||||||
| е | m | 2m | 1/3m | - | - | - | - | 0,15 | 0,20 | ||||||
| ж | m | 1,5 m | 3/2m | - | - | - | - | 0,15 | 2,5 | ||||||
| з | m | m | 1/4m | - | - | - | - | 0,20 | 0,15 | ||||||
| и | m | 3m | 5m | - | - | - | - | 0,15 | 0,20 | ||||||
| к | m | 1/3m | 1/5m | 1/5m | - | - | - | - | - | 0,12 | - | 2,5 | |||
| а | m | 2m | 1/3m | m | - | - | - | - | - | 0,20 | - | 1,75 | |||
| б | m | 1/4m | 1/5m | - | - | - | 0,12 | 0,25 | 1,5 | ||||||
| в | m | 3m | 1/8m | 1/2m | - | - | - | - | - | 0,12 | - | ||||
| г | m | 1/4m | 1/6m | - | - | - | 0,18 | 0,15 | 1,5 | ||||||
| д | m | ½ m | 1/10m | m | - | - | - | 0,15 | - | 2,5 | |||||
| е | m | 4m | 1/2m | - | - | - | - | 0,20 | 0,25 | 1,8 | |||||
| ж | m | 3m | m | - | - | - | - | 0,20 | |||||||
| з | m | 1/3m | 1/2m | - | - | - | - | 0,15 | 0,25 | 2,5 | |||||
| и | m | 2m | 7m | - | - | - | - | 0,20 | 0,15 | ||||||
| к | m | ½ m | 1/4m | 1/6m | - | - | - | - | - | 0,15 | - | ||||
Пример выполнения задания:
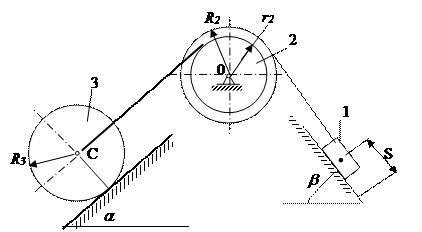
Дано: m1 – масса груза 1, m2 = 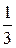 m1, m3 = 2m1, R2 =20 см, R3 = 30 см, r2 = 15 см, i2x =17 см, a 300, b = 600, f = 0,2, d = 0,25 см, S = 6 м. Каток 3 – однородный сплошной цилиндр. На рисунке Д-2.1,а показана механическая система в начальном положении.
m1, m3 = 2m1, R2 =20 см, R3 = 30 см, r2 = 15 см, i2x =17 см, a 300, b = 600, f = 0,2, d = 0,25 см, S = 6 м. Каток 3 – однородный сплошной цилиндр. На рисунке Д-2.1,а показана механическая система в начальном положении.
 Найти
Найти 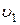 - скорость груза 1 в конечном положении.
- скорость груза 1 в конечном положении.
Рисунок 3
Схема механизма в начальном положении
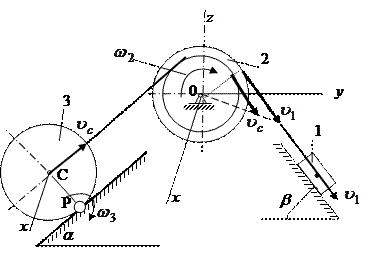 |
Рисунок 4
Схема скоростей точек.
 |
Рисунок 5
Схема сил, действующих на механическую систему.
Р е ш е н и е:
Применим теорему об изменении кинематической энергии системы:
Т-Т0 = 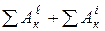 , (1)
, (1)
где Т и Т0 – кинетическая энергия системы в начальном и конечном положениях;
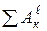 - сумма работ внешних сил, приложенных к системе, на перемещении системы из начального положения в конечное;
- сумма работ внешних сил, приложенных к системе, на перемещении системы из начального положения в конечное;
 - сумма работ внутренних сил системы на том же перемещении.
- сумма работ внутренних сил системы на том же перемещении.
Для рассматриваемой системы, состоящей из абсолютно твердых тел, соединенных нерастяжимыми нитями,
 = 0.
= 0.
Так как в начальном положении система находится в покое, то Т0 = 0.
Следовательно, уравнение (1) принимает вид
Т0 = 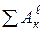 . (2)
. (2)
Для определения кинетической энергии Т и суммы работ внешних сил
надо изобразить систему в конечном положении (рисунок 4-5).
Напишем кинематические соотношения между скоростями и перемещениями точек системы, т.е. уравнения связей, при этом скорости и перемещения выразим соответственно через скорости и перемещения груза 1.
Вращательная скорость точек обода каждого из барабанов 2 равна скорости движения сходящей с барабана нити (рисунок 4).
Следовательно,
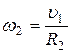 и
и 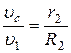 ,
,
где 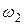 - угловая скорость барабанов,
- угловая скорость барабанов,
 - скорость центра тяжести С катка 3.
- скорость центра тяжести С катка 3.
 . (3)
. (3)
Так как каток 3 катится без скольжения, то мгновенный центр скоростей катка находится в точке Р. Поэтому угловая скорость катка 3 равна
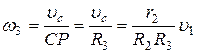 . (4)
. (4)
Вычислим кинетическую энергию системы в конечном положении как сумму кинетических энергий тел 1, 2, 3:
Т = Т1 + Т2 + Т3. (5)
Кинетическая энергия груза 1, движущегося поступательно,
Т1 = 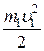 .
.
Кинетическая энергия барабанов 2, вращающегося вокруг неподвижной оси,
Т2 = 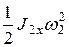 ,
,
где  - момент инерции барабанов относительно оси вращения ОХ:
- момент инерции барабанов относительно оси вращения ОХ:
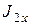 = m2
= m2 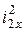 .
.
Кинетическая энергия катка 3, совершающего плоское движение,
Т3 = 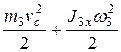 ,
,
где  - момент инерции катка 3 относительно его центральной оси СХ:
- момент инерции катка 3 относительно его центральной оси СХ:
 =
= 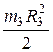 .
.
Подставляя заданные значения масс, моментов инерции, найденные величины  ,
,  и
и 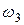 в выражение (5) получаем следующее значение кинетической энергии системы
в выражение (5) получаем следующее значение кинетической энергии системы
Т = 
или
Т = 2,93 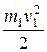 . (6)
. (6)
Найдем сумму работ всех внешних сил, приложенных к системе на заданном ее перемещении. Покажем внешние силы, приложенные к системе (рисунок 5).
Работа силы тяжести 
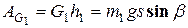 . (7)
. (7)
Работа нормальных реакций 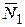 и
и  равна нулю.
равна нулю.
Работа силы трения скольжения 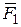
 .
.
Так как
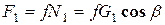 ,
,
то
 . (8)
. (8)
Силы 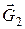 ,
,  и
и  не производят работы, так как они приложены к неподвижной точке.
не производят работы, так как они приложены к неподвижной точке.
Работа силы 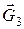
 , (9)
, (9)
где Sc – перемещение центра тяжести катка.
Работа силы Fcц равна нулю, так как она приложена в мгновенном центре скоростей.
Работа пары сил сопротивления качению катка 3
Амс = - Мс 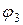 ,
,
Мс = d N3 = d G3 cosa - момент пары сил сопротивления качению;
где 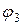 – угол поворота катка 3.
– угол поворота катка 3.
Таким образом,
Амс = - d m3 g cos a . 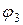 (10)
(10)
Сумма работ всех внешних сил определяется сложением работ, вычисляемых по формулам (7, 8, 9, 10):
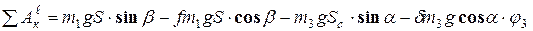 (11)
(11)
Перемещение центра тяжести катка Sc и угол поворота 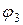 выразим через перемещение груза S. Так как линейные (или угловые) перемещения находятся в такой же зависимости, как линейные (или угловые) скорости, то в соответствии с формулами (3) и (4), получаем:
выразим через перемещение груза S. Так как линейные (или угловые) перемещения находятся в такой же зависимости, как линейные (или угловые) скорости, то в соответствии с формулами (3) и (4), получаем:
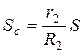 и
и  .
.
Подставим эти значения в выражение (11):
 ,
,
или
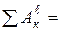 0,004 m1gS. (12)
0,004 m1gS. (12)
Ссогласно теореме (2), приравниваем значения Т и 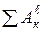 , определяемые по формулам (6) и (12):
, определяемые по формулам (6) и (12):
2,93  = 0,004 m1gS,
= 0,004 m1gS,
откуда
v1 = 0,40 м/с.
3.4 СПИСОК ЛИТЕРАТУРЫ
1 Никитин Н.Н. Курс теоретической механики. М.: Высшая школа, 1990
2 Тарг С.М. Краткий курс теоретической механики. М.: Высшая школа, 1998
3 Яблонский А.А., Никифорова В.М. Курс теоретической механики. Ч. 1,2, Санкт-Петербург, изд. «Лань», 1998
4 Бутенин Н.В., Лунц Я.Л., Меркин Д.Д. Курс теоретической механики. Т. 1,2, Санкт-Петербург, Изд. «Лань», 1998
5 Мещерский И.В. Сборник Задач по теоретической механике. М.: высшая школа, 1985
6 Сборник заданий для курсовых работ по теоретической механике. Под ред. А.А.Яблонского,М.: ВШ – 1972
7 Теоретическая механика. Методические указания и контрольные задания для студентов-заочников строительных, транспортных, машиностроительных и приборостроительных специальностей высших учебных заведений. Под ред. С.М.Тарга, М.:ВШ – 1982
8 Синдеев П.Р. Методические указания, рабочая программа, контрольные задачи и задания на курсовые работы по теоретической механике для студентов-заочников специальности 1902 «Подземная разработка месторождений полезных ископаемых». Усть-Каменогорск, 2001
9 Есипенко Л.П., Синдеев П.Р. Теоретическая механика. Методические указания и задания. Усть-Каменогорск, 2000
10 Бать М.И., Джанелидзе Г.Ю., Кельзон А.С. Теоретическая механика в примерах и задачах. Ч. 1, 2. М., 1961 и последующие издания.