Закон сохранения импульса. Реактивное движение
При взаимодействии тел импульс одного тела может частично или полностью передаваться другому телу. Если на систему тел не действуют внешние силы со стороны других тел, то такая система называется замкнутой.
В замкнутой системе векторная сумма импульсов всех тел, входящих в систему, остается постоянной при любых взаимодействиях тел этой системы между собой.
Этот фундаментальный закон природы называется законом сохранения импульса. Он является следствием из второго и третьего законов Ньютона.
Возьмем замкнутую систему из двух взаимодействующих тел. Силы F1 и F2 это силы взаимодействия между телами. Третий закон Ньютона гласит, что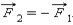 
Пусть тела взаимодействуют во течение времени t. Тогда импульсы сил одинаковы по модулю и противоположны по направлению, как и сами силы.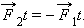 
Применим к телам второй закон Ньютона: 
Здесь 
и 
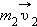→ - скорости тел в конце взаимодействия. Соответственно, обозначения без штрихов - скорости в начальный момент взаимодействия.
Из записанного выше следует соотношение: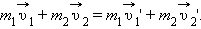 
Это равенство - математическая форма записи закона сохранения импульса. Оно означает, что суммарный импульст системы в результате какого-то взаимодействия не изменился.
Закон сохранения импульса во многих случаях позволяет находить скорости взаимодействующих тел даже тогда, когда значения действующих сил неизвестны. Примером может служить реактивное движение.
При стрельбе из орудия возникает отдача – снаряд движется вперед, а орудие – откатывается назад. Снаряд и орудие – два взаимодействующих тела. Скорость, которую приобретает орудие при отдаче, зависит только от скорости снаряда и отношения масс (рис. 1.17.2). Если скорости орудия и снаряда обозначить через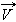 
и 
а их массы через M и m, то на основании закона сохранения импульса можно записать в проекциях на ось OX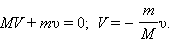 
|
|
На принципе отдачи основано реактивное движение. В ракете при сгорании топлива газы, нагретые до высокой температуры, выбрасываются из сопла с большой скоростью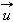 
относительно ракеты. Обозначим массу выброшенных газов через m, а массу ракеты после истечения газов через M. Тогда для замкнутой системы «ракета + газы» на основании закона сохранения импульса (по аналогии с задачей о выстреле из орудия) можно записать:
|
где V – скорость ракеты после истечения газов. В данном случае предполагается, что начальная скорость ракеты равнялась нулю.
Полученная формула для скорости ракеты справедлива лишь при условии, что вся масса сгоревшего топлива выбрасывается из ракеты одновременно. На самом деле истечение происходит постепенно в течение всего времени ускоренного движения ракеты. Каждая последующая порция газа выбрасывается из ракеты, которая уже приобрела некоторую скорость.
2. КПД обратного обратимого цикла Карно – холодильная машина.
Цикл Карно с протеканием процессов против часовой стрелки называется обратным. Это цикл холодильных машин и тепловых насосов.
Холодильная машина – это машина, работающая по обратному циклу Карно (рис. 5.4). То есть если проводить цикл в обратном направлении, тепло будет забираться у холодильника и передаваться нагревателю (за счет работы внешних сил).
Обратный цикл Карно можно рассмотреть на примере рис. 5.5. При изотермическом сжатии В–А, от газа отводится количество теплоты Q1 при Т1. В процессе изотермического расширения D–С к газу подводится количество теплоты Q2.
|
|
В этом цикле 
, 
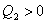и работа, совершаемая над газом, отрицательна, т.е.
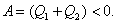
| (5.5.3) |
Если рабочее тело совершает обратный цикл, то при этом можно переносить энергию в форме тепла от холодного тела к горячему за счет совершения внешними силами работы.
Для холодильных машин, работающих по циклу Карно
КПД идеальной тепловой машины, работающей по обратному циклу Карно,
КПД реальной тепловой машины, работающей по обратному циклу Карно,
По обратному циклу Карно работают все холодильные машины. |
.
.
.
10. Уравнение динамики вращательного движения твердого тела относительно неподвижной оси. (В ПРИНЦИПЕ НУЖНО ТОЛЬКО КРАСНЕНЬКИМ, И ТО ТАМ МНОГО, ОСТАЛЬНОЕ ДЛЯ ОБЩЕГО РАЗВИТИЯ J)
Пусть твердое тело вращается вокруг неподвижной оси О–О¢. Разобьем это тело на элементарные учатски mi. Выбираем произвольную материальную точку, принадлежащую этому телу. Точка вместе с вращающимся телом описывает окружность. Проведем от точки линию и обозначим ее ri. Приложим к точке силу Fi.
Под действием силы`Fi, направленной перпендикулярно к оси по касательной к окружности, описываемой материальной точкой, движущаяся точка начнет вращательное движение. По второму закону Ньютона
, 
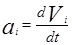. (10)
Используем формулу, устанавливающую связь между линейной и угловой скоростью
, (11)
где w – угловая скорость; у всех точек вращающегося тела она одинакова.
|
|
Подставим значение линейной скорости в формулу ускорения
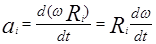. (12)
Подставим значение ускорения во второй закон Ньютона
, (13)
умножим обе части последнего равенства на Ri и просуммируем его
, (14)
где 
– момент силы;
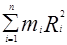– момент инерции;
– угловое ускорение.
(15)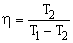